课堂巧切西瓜 验证飞行方向
浙江省永康第一中学(321300) 沈海燕
课堂巧切西瓜 验证飞行方向
浙江省永康第一中学(321300) 沈海燕
在高二区域地理的“地球和地图”一节内容时,学生在判断飞机的飞行方向时,由于缺乏空间想象能力,对于“如何确定同一纬度的两点之间的飞行方向”往往百思不得其解。经过调查了解,发现学生还没有接触到立体几何中的大圆概念。不理解大圆的概念,又怎么能理解“球面上任意两点的最短距离,是过这两点的大圆的劣弧”呢?
因为在学习这部分内容时,恰逢西瓜上市,于是我决定用“西瓜”这个特殊的教具来帮助学生理解“球面上任意两点的最短距离,是过这两点的大圆的劣弧”,从而搞清“同一纬度的两点之间的飞行方向”。
师:首先我们得搞清楚一个概念,什么是大圆?所谓大圆即“球面大圆”,球面上圆心与球心重合的圆。球面上任意两个大圆相互等分。虽然在数学中我们还未学到大圆的概念,但其实平时我们切西瓜时,基本上就是按大圆来切的。请问,可以有多少种切法?
生:无数种。因为只要过西瓜的中心就是大圆。
师:下面我们请一个同学上来切西瓜。(必须是大圆)
(生情绪激昂,个个跃跃欲试,很快有个男同学走上讲台,成功地把西瓜切成等分的两个大圆。)
师:那么在地球上,有哪些大圆?
生1:赤道。
生2:任意一个经线圈都可以说是一个大圆。
师:很棒!球面上两点的最小距离为经过两点的大圆的劣弧。航海与航空中利用这一原理而设置了大圆航线。下面我们就讨论一下,两点间的飞行方向问题。
师:如果两点同在一条经线圈,那么飞行方向如何确定呢?请先说明方向,再用图说明。
学生在下面讨论的很热烈,还不时地用笔画图。
生1(边看着西瓜边比划):若两点同在一条经线圈且同位于北半球,根据“球面上两点的最小距离为经过两点的大圆的劣弧”,最近航程一定是先向北,过极点后,再向南。(讲完后让学生在黑板上画板图。)
生2(受到生1启发后):若两点同在一条经线圈且同位于南半球,根据“球面上两点的最小距离为经过两点的大圆的劣弧”,最近航程一定是先向南,过极点后再向北。
(讲完后让学生在黑板上画板图。)
师:若两点同在一条经线圈但不在同一半球呢?
生3(看了看西瓜,然后喜形于色):若两地位于不同半球,这时需要讨论,确定过哪个极点的为劣弧,再讨论。
师:这位同学相当聪明!的确应该讨论一下。看来看着西瓜画图,效果是相当好啊!
师:若两点同在北纬40度,请大家讨论一下自A到B的飞行方向?请大家看图,考虑如何确定过两点的大圆。

生1(迫不及待地举手):这还不简单,一定是自正西向正东,我来演示一下。
(说完就到讲台上来了,他先确定了两点同在北纬40度,然后沿着北纬40度纬线方向切下去,切完后傻眼了,他拿着切好的一个小圆在台上傻笑,下面同学更是笑翻天,“你切的哪里是大圆啊,像个小瓜皮帽,自己戴上吧!”)
师:刚才这位同学的勇气确实可嘉,他牺牲了小我,但为其他同学创造了成功的条件。下面哪位同学上来和他一起再来切切。
生2:既然是要切大圆,就必须让这两点和西瓜的球心在同一个圆上。
(学生们在讲台上切着西瓜,下面同学都围上来,他们一致发现过这两点的大圆并不是沿着原先的纬线,而是在纬线的北方的一条弧线。)
师:下面我们请一位同学来说说A点到B点的飞行方向。
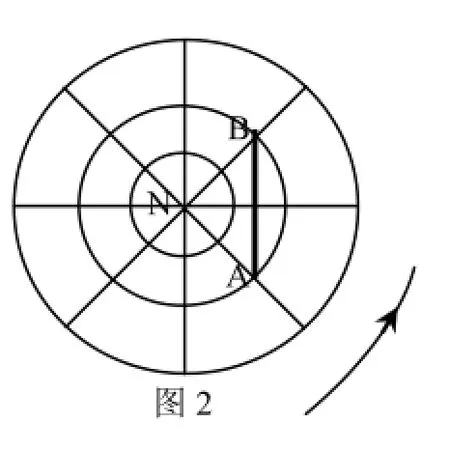

生1(看着西瓜的弧线,边比划边说):一定不是自正西向正东飞行,应该是条弧线,应该先向东北飞,然后再向东南飞。
师:谁能在图2中画出刚才的切线?
(生小心翼翼地画出图2中的小短横)
师(用图归纳,强化认知):说得很好,画得更好。我们来看看图3,其实这两幅表达的内容是相同的。刚才同学切的大圆就是图中ABO所在的大圆,从图3中能更直观地看到,飞机的飞行方向是弧线,而且飞行方向有一定的规律可循,同学们讨论后再发言。
生2:一般是先向高纬度方向,再向低纬度方向。
师:我们来验证一下他所说的规律是否可行。
若两点同在南纬40度,则如何来描述飞机自C到D的飞行方向呢?
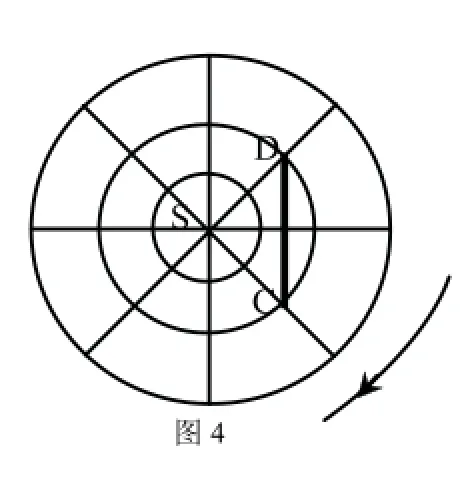
生3:自C到D的飞行方向是,先向西南方向飞再向西北方向飞。

