HPRF PD 末制导雷达解距离模糊方法设计
王 莹,苏宏艳,朱淮城,袁 起
(1.中国航天科工集团二院 二十五所, 北京100854;2.中国航天科工集团第二研究院,北京100854)
1 引 言
距离模糊问题是高重频脉冲多普勒(HPRF PD)末制导雷达的固有问题,当目标的回波延迟时间大于发射脉冲的重复周期时,会产生距离模糊。目前,解决距离模糊的方法主要采用多脉冲重复频率测距法。该方法测距精度高,在杂波附近的目标检测能力强[1]。距离遮挡问题是HPRF PD 末制导雷达的另一固有问题,PD 体制末制导雷达通过“时分”的方法发射和接收信号[2]。在发射机发射脉冲期间接收机必须关机。如果目标回波到达末制导雷达的时候正赶上发射机发射脉冲,末制导雷达不能接收到目标回波信号而处于“遮挡区”。随弹目距离接近,距离遮挡周期性变化。可以根本解决“距离遮挡”问题的方法是多重PRF 切换法。切换PRF 的最可靠依据是在弹目交会过程中测得准确的弹目距离R[3]。
通过对PD 体制下“距离模糊”及“距离遮挡”问题进行分析,可以看出两者是相互制约的。要从根本上解决遮挡问题,必须提前测得弹目距离R,而在HPRF PD 体制下,测得弹目距离需要利用多重PRF法解距离模糊,在解模糊时发射的多重PRF 信号极有可能由于处于“遮挡区”而无法检测到目标回波,造成解距离模糊失败。众多学者对于解距离模糊和抗距离遮挡问题分别进行了大量的研究[4-6],但对同时解决两种问题的方法却研究较少。针对以上情况,如何解决HPRF PD 末制导雷达在距离遮挡环境下的解距离模糊问题有待研究。本文对于发射机发射的多重PRF 信号进行设计,从而保证发射信号的遮挡区相互交替,确保了在末制导雷达作用距离范围内除弹目相遇段以外的任意距离段均可接收到至少N(N ≥3)个重频的回波信号,即可用接收到的回波信号解模糊,再利用测得的弹目距离完成抗遮挡重频切换并进行目标跟踪。
2 无距离遮挡影响的多PRF 法解距离模糊的参数设计
现阶段利用多PRF 法解模糊发射信号的参数设计关系可表示为
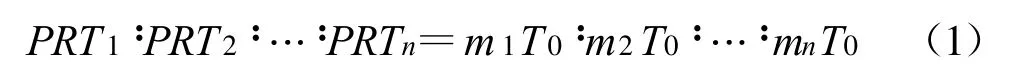
式中, PRTi表示各发射信号的脉冲重复周期;mi表示各脉冲重复周期间的比值;T0表示各脉冲重复周期的最大公约数,称为基准重频脉冲重复周期[7]。
对于末制导雷达解模糊发射信号脉冲重复频率的选取要求总结如下:
(1)发射信号脉冲重复频率的选取决定了该脉冲重复频率发射信号测距、测速的不模糊范围、遮挡区的分布,应当根据末制导雷达的具体要求综合考虑确定;
(2)发射信号脉冲重复频率的选取还应当满足:在脉冲宽度τ确定时,经过相参积累、非相参积累后,该发射信号的最大作用距离R 应当大于末制导距离Rmax;
(3)在利用多个脉冲重复周期的发射信号解模糊时,还要求接收到的任意N 个脉冲重复周期回波信号的最大解模糊范围大于末制导距离Rmax。
以上参数设计准则是在不考虑距离遮挡现象的影响前提下提出的多重PRF 解模糊时的发射信号设计准则,当存在距离遮挡时,以上参数设计原则需要重新修正。
3 遮挡环境下多重PRF 法解距离模糊的参数设计
本文对于距离遮挡环境下多重PRF 法解模糊时的发射信号进行设计,设计准则如下。
3.1 遮挡环境下多重PRF 法解模糊发射信号基准重频T0 的设计
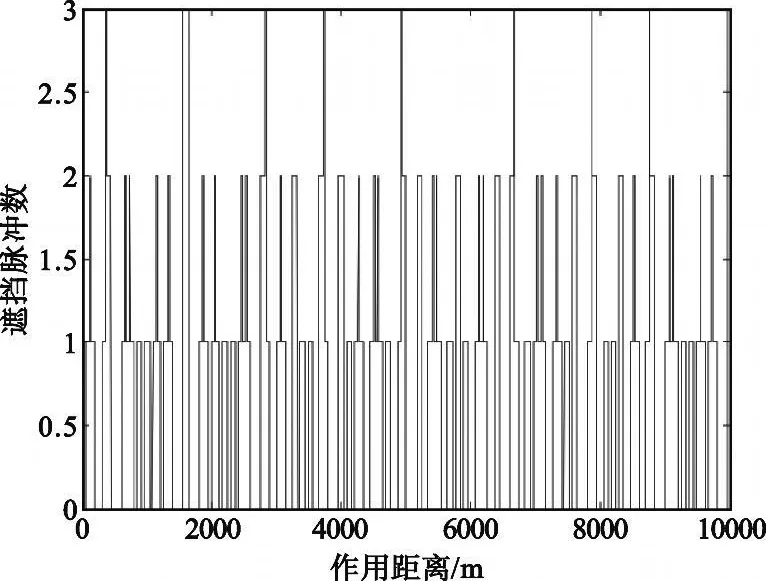
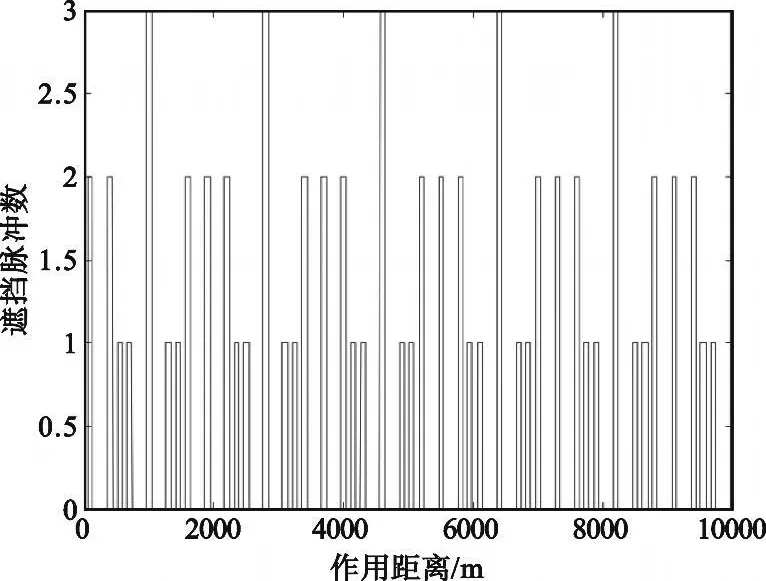
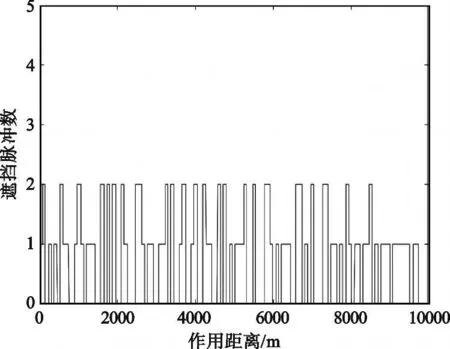
在遮挡环境下解模糊时,应当避免目标在解模糊发射的所有脉冲串上均被遮挡的情况[4]。假设发射两个脉冲串解模糊,脉冲串的重复周期分别为:PRT1=m1T0, PRT2=m2T0,其中m1、m 2 互素。显然,目标时延的不模糊范围是0 ~m1m2T0。假设目标时延为t(0 ≤t 式中,x1、x2 表示两个PRF 信号归一化后的模糊距离。 图1 回波脉冲不可见的情况Fig.1 Situation that return signal can′t be received 则目标在每个脉冲串上均不可见的情况可以表示为 此时有两种可能: (1)若τ 此时: 即当模糊度k1、k 2 满足时,才会出现目标在所有回波脉冲均不可见的情况。当解模糊脉冲数大于2 时,目标完全被遮挡的可能性更小; (2)若τ>T0,则mτ>1,此时会导致[ x1] 、[ x2]可以取多值,目标遮挡区扩散。此情况对于目标抗遮挡、解模糊性能会产生较大的影响。 本文通过计算机仿真对以上分析进行了验证。选择两组三重脉冲重复周期的发射信号,两组信号脉冲重复周期比值相同,均为:PRT1∶PRT2∶PRT3=4T0∶5T0∶7T0,令发射信号脉冲宽度τ=0.5 μs。在第一组信号中取T0=0.4 μs,T0<τ。在第二组信号中取T0=0.5 μs, T0=τ。在末制导距离不断减小的过程中,则两组发射信号的遮挡区分布图如图2 和图3 所示。 图2 基准重频T 0<τ时的遮挡区分布Fig.2 Distribution of eclipse area when reference PRT T0<τ 图3 基准重频T 0=τ时的遮挡区分布Fig.3 Distribution of eclipse area when reference PRT T0=τ 通过仿真分析可以看出,当基准重频T0≥τ时,有效地抑制了遮挡区扩散,避免了回波信号同时被遮挡的现象发生。因此,在设计参数时应当令基准重频T 0 满足T0 ≥τ,在此参数设定条件下,发射信号全部被遮挡的概率极小。 下面分析在距离遮挡的影响下,发射信号脉冲重复周期间比值mi 应当如何选取。 当多重PRF 法中发射信号脉冲重复周期间的比值mi不互素时,同样可以完成解模糊。但是,此种情况使各信号脉冲重复周期的最小公倍数减小,产生相同余数的情况大大增加。例如PRT1∶PRT2∶PRT3=4T0∶6T0∶8T0,当目标回波时延t ∈(12T0~16T0),PRT1、PRT2两个回波信号具有相同的余数,即模糊距离测量值相同。在距离遮挡的影响下,两个回波信号将同时落入遮挡区或非遮挡区。当目标回波时延t ∈(8T0~12T0),PRT1、PRT3产生相同的余数,两个回波信号同时进入遮挡区或非遮挡区。当目标回波时延t ∈(24T0~28T0), PRT1、PRT2、PRT3产生相同的余数,则3 个回波信号同时进入遮挡区或非遮挡区。从发射多脉冲重复频率信号抗遮挡的策略出发,应当使各脉冲重复频率的回波信号的遮挡区相互交替。因此,减小回波信号同时进入遮挡区的情况,应当尽量增大任意两脉冲重复周期信号的最小公倍数,选择任意两脉冲重复周期间比值互素的发射信号。例如:PRT1∶PRT2∶PRT 3 =4T0∶5T0∶7T0,当目标回波时延t ∈(20T0~24T0),PRT1、PRT2 两个回波信号产生相同的余数,则两回波信号同时落入遮挡区或非遮挡区。当目标回波时延t ∈(35T0~39T0),PRT1、PRT 3 产生相同的余数,两回波信号同时进入遮挡区或非遮挡区。当目标回波时延t ∈(140T0~144T0),PRT1、PRT2、PRT3产生相同的余数,则三回波信号同时进入遮挡区或非遮挡区。 本文通过计算机仿真对以上分析进行了验证。分别选择两组三重脉冲重复周期的发射信号,第一组各脉冲重复周期间的关系为:PRT1∶PRT2∶PRT3=4T0∶6T0∶8T0,第二组各脉冲重复周期间的关系为:PRT1∶PRT2∶PRT3=4T0∶5T0∶7T0。第一组发射的信号中3 个发射信号间的脉冲重复周期比值非互素,第二组发射信号中3 个发射信号间脉冲重复周期的比值互素。在末制导距离不断减小的过程中,两组发射信号的遮挡区分布如图4 和图5 所示。 图4 脉冲重复周期比值非互素的遮挡区分布Fig.4 Distribution of eclipse area when the ratio of PRT is even 图5 脉冲重复周期比值互素的遮挡区分布Fig.5 Distribution of eclipse area when the ratio of PRT is prime 观察仿真结果可以看出,由于非互素的脉冲重复周期信号同时被遮挡或未被遮挡的情况明显多于互素的脉冲重复周期信号,因此选择发射信号脉冲重复周期比值互素的信号可以增大任意两发射信号的最小公倍数,减小使各发射信号得到相同余数的距离段,大大减小回波信号同时被遮挡的概率。基于在距离遮挡的环境下解模糊的指导思想是在末制导过程中的任意距离段均可收到回波信号,因此,在距离遮挡环境下不论采用哪种多重PRF 法解模糊均应选择脉冲重复周期比值互素的发射信号进行解模糊。 对于参数设计准则进行仿真验证,发射信号脉冲宽度τ=0.5 μs,考虑距离遮挡的影响,测距时发射5 种PRF 信号,根据上文的参数设计方法,对发射信号脉冲重复周期进行设计: (1)要求T0≥τ,应令T 0 ≥0.5 μs,这里取T0=0.5 μs; (2)PRT1∶PRT2∶…∶PRT 5 =m1T0∶m2T0∶…∶m5T0,要求m1,m2, …,m5互素。可令: 或令 然而,当m1∶m2∶…∶m5=1∶3∶4∶5∶7 时,在仅接收到PRT1∶PRT2∶PRT3=1T0∶3T0∶4T0 三重回波信号的距离段内,这3 个PRF 信号的最大解模糊距离为:R=(c/2)·m1m2m3T0≤Rmax,因此应当选择:m1∶m2∶…∶m5=4∶5∶7∶9∶11,满足任意3 个PRF 信号的最大解模糊距离大于Rmax的要求。 将设计后的T0 及mi 代入,得到五重PRF 解模糊信号的脉冲重复周期分别是:PRT1=2 μs, PRT2=2.5 μs, PRT3=3.5 μs, PRT4=4.5 μs, PRT5=5.5 μs。对这5 个PRF 信号在末制导过程中的距离遮挡情况进行仿真,距离遮挡图如图6 所示。 图6 利用遮挡环境下解模糊参数设计方法设计的PRF 信号遮挡区分布图Fig.6 Distribution of transmitting signals eclipse area which is designed with rule of range ambiguity resolving in the condition of range eclipse 观察信号遮挡区分布图可以看出,除弹目相遇处的遮挡现象无法避免外,其它区域均满足存在任意三重PRF 信号未被遮挡的要求。即在末制导过程中的任意位置均可利用多重PRF 法解距离模糊得到弹目距离,利用弹目距离信息,即可求出末制导跟踪过程中发射信号的遮挡区分布情况,从而彻底解决距离遮挡对于末制导过程中探测跟踪目标的影响。 本文提出在距离遮挡影响下利用发射多重PRF信号解模糊的方法,并对发射信号的参数设计准则进行分析,从而保证在末制导过程中除弹目相遇段外的任意位置均可实现无模糊测距。根据得到的距离信息可以提前预测各重PRF 信号的遮挡区分布,切换重频抗遮挡,确保目标的正常跟踪。通过仿真验证,本设计方法可以有效完成在距离遮挡环境下的解距离模糊任务,消除距离遮挡和距离模糊现象对于HPRF PD 体制末制导雷达探测跟踪目标性能的影响。本方法实现简便,可靠性强,具有较强的工程应用价值。如何在末制导环境下提高现有方法的解模糊性能有待进一步研究。 [ 1] 曹宇飞, 屈晓光.脉冲多普勒雷达解模糊方法分析[ R]//航天报告.北京:[s.n.] , 2006. CAO Yu -fei, QU Xiao -guang.Analysis of Ambiguity Resolution in Pulse Dopp ler radar[ R]//Aerospace Report.Beijing:[ s.n.] ,2006.(in Chinese) [ 2] 张筱靖.毫米波导引头信号处理技术研究[ D] .北京:航天二院,2008. ZHANG Xiao-jing.Study on Signal Processing Technology of MMW Seeker[D] .Beijing:The Second Academy of China Aerospace, 2008.(in Chinese) [ 3] 李建彬,夏桂芬.高重频PD 雷达导引头抗距离遮挡技术[ J] .电讯技术, 2008,48(10):41-44. LI Jian-bin, XIA Gui-fen.A voidance Eclipse for HPRF PD Radar Seeker [ J] .Telecommunication Engineering,2008,48(10):41-44.(in Chinese) [ 4] 谢峰.中脉冲重复频率解模糊研究[ D] .北京:航天二院, 1998. XIE Feng.Study on Ambiguity Resolution with MPRF[ D] .Beijing:The Second Academy of China Aerospace, 1998.(in Chinese) [ 5] Trunk G, Brockett S.Range And Velocity Ambiguity Resolution[C]//Proceeding of IEEE National Conference on Radar.[S.l.] :IEEE,1993:146-149. [ 6] 雷文,龙腾, 曾涛,等.一种脉冲多普勒解距离模糊的新方法[ J] .北京理工大学学报, 1999, 19(3):357-360. LEI Wen, LONG Teng, ZENG Tao, et al.The Resolution of Range Ambiguity in a Medium Pulse Doppler Radar[ J] .Journal of Beijing Institue of Technology,1999, 19(3):357-360.(in Chinese) [7] 周闰, 高梅国,戴擎宇, 等.余差查表法解单目标距离模糊的分析与仿真[J] .系统工程与电子技术,2002,24(5):30-32. ZHOU Run, GAO Mei-guo, DAI Qing-yu, et al.Analysis and simulation for Ambiguity Resolving Using Residues'Difference Look -up Table[ J] .Systems Engineering and Electronics, 2002,24(5):30-32.(in Chinese) [8] 段军棋, 何子述, 韩春林.高效的PD 雷达多重频模糊分辨算法[ J] .电子科技大学学报,2008, 37(4):549-551. DUAN Jun-qi, HE Zi-shu, HAN Chun-lin.Computation Efficient Algorithm for Resolving Range and Velocity Ambiguities in Multiple PRF PD Radars[J] .Journal of University of Electronic Science and Technology of China, 2008, 37(4):549-551.(in Chinese)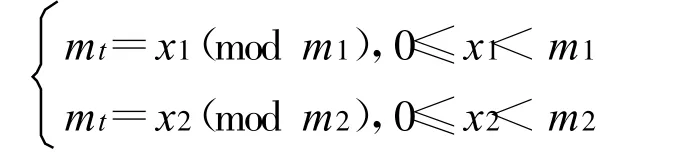

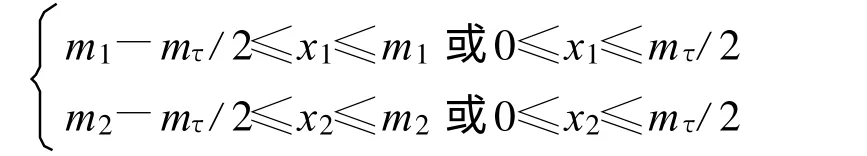
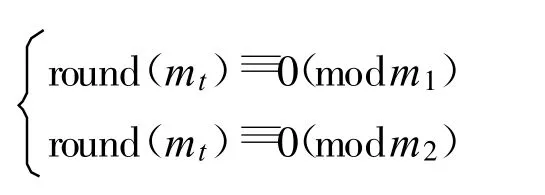


3.2 遮挡环境下脉冲重复周期间比值mi 的选取

4 仿真验证
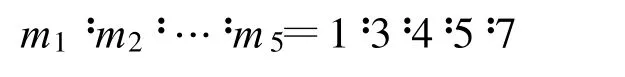
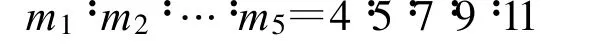
5 结 论
