细线浮标最佳长度数学模型的建立

李成辉,乔万亮,高淑清

(绥化水文局,黑龙江绥化 152053)

在河流测验中,其中一个重要测验项目就是断面流向测验。在河流某一河段上垂直流向布设一个横断面用来进行流量和沙量等测验,这就需要我们首先要进行这一河段的流向测量,然后才能确定横断面的位置与方向。若对于已经布设好的某一测验横断面,也要对其进行该断面流向测验校核。断面流向是指水流方向与断面线的垂直方向线之间的夹角。对于天然河流流向测量仍采用水面浮标方法进行,其中细线浮标法是一种简便易行的用来进行流向变化测验校核的有效方法。特别是对一些有过河索、缆道、缆车施测流量的水文站,非常适用。细线浮标的细线长度多长怎样来确定为最佳长度?虽说《河流流量测验规范》上明确给出是20 m,但是,对于不同宽度的河流来说只规定了这一数值是不充分的。本文正是从这种情况下进行了创建数学模型、深入进行分析研究和充分论证。

1 细线浮标

1.1 概念

细线浮标是在水面上一个已知长度的细线一头连接到测速垂线的水面交界处,另一头系一个浮鱼随水流自然漂浮在下游,用来进行测验断面流向的工具。

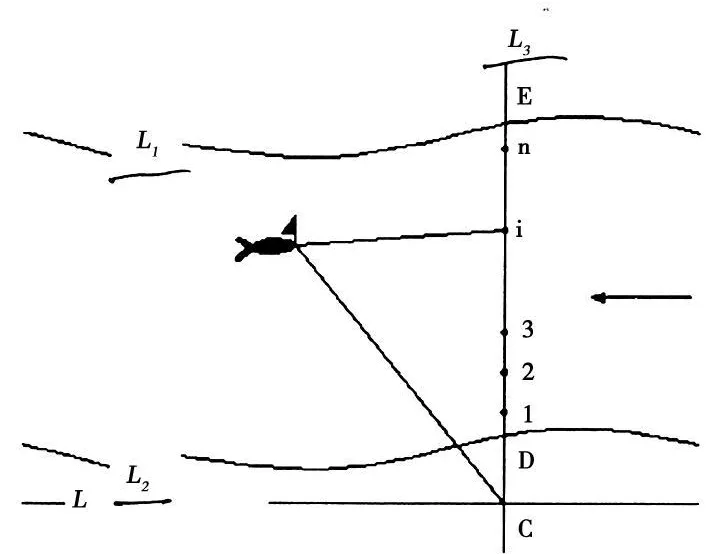
图1 细线浮标测验流向平面简图

1.2 应用

图1就是细线浮标测验流向的平面简图。图中线段 L 1和线段L 2是一条河流的两岸岸边线,箭头线代表水流方向,线段L是岸上所设基线,线段 L 3是流量测验断面线,断面线上的D E长度为河宽,断面线上的点1、2、3、…、i、…、n是测速垂线位置,也是细线浮标左右偏离角度测量的点。

利用细线浮标测验断面流向需要与经纬仪或全站仪等一起共同来完成。把经纬仪设在岸上基线与断面线交点上,测出浮鱼位置或视线与断面线间的角度,就可算出流向与断面垂直方向间的角度即流向偏角。

2 数学模型

2.1 模型创建

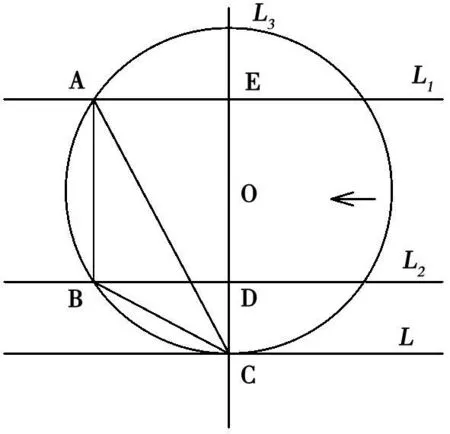
图2 模型创建图

根据图 1的内容进行建模,见图 2,其中 3条直线 L、L1、L2是互相平行的,直线 L3与 3条直线 L、L1、L2垂直相交,交点分别是E、D、C 3点。O点是线段E D中点,以O点为圆心以O C为半径作圆,分别交直线L1、L2于A、B两点,连接弦A B、C B、C A,这样就有弦A B平行于L3。L是圆O的切线,而且C是切点。图形建立起来之后,我们就此图利用细线浮标施测流向作以说明:把L1、L2分别看作是河流两岸的水边线,图上的箭头指的是水流方向,L3是测验水流要素的横断面线,水面宽为 E D线段,L可以看作是一条基线,C是水文测量高程基点,即架设经纬仪等仪器的固定点,而线段C B、C A是提供测量细线浮标两岸水边点视线。A B线段是细线浮标的浮鱼测量每条线时经过平均位置的连线。A B线段可以沿上游或下游进行平行滑动,当滑动到某一位置时,使∠A C B最大,如果左右岸测量角度最大,确定浮鱼位置其精度会最高。A E或 B D就是细线在其上面的投影长度,是浮鱼所处位置到断面E D最佳距离。如何证明A B所处什么位置能使∠A C B最大这个问题需要以下证明。

2.2 证明

1)当A B线段平移滑动到其左面A1B1位置时,构成了三角形A1B1C,如见图 3。这里需要证明的是:∠A C B＞∠A1C B1是否成立?过A点作 A C1直线与切线L交于C1点,则

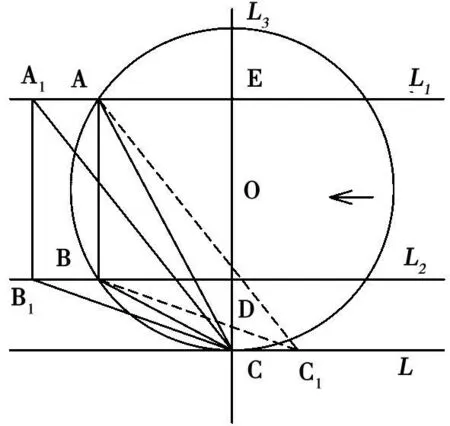
图3 计算简图

∵ A1A∥C C1A C1∥A1C

∴ A C1=A1C A1A=C C1

连接线段B C1,

∵A1A∥B1B 且A1A=B1B

又∵A1A∥C C1且A1A=C C1

∴B1B∥C C1且B1B=C C1

也就是说,在平行四边形B1B C1C中,有B1C∥B C1B1C =B C1

∵A1B1=A B

∴△A1C B1与△A C1B是两个全等三角形

∠A C1B=∠A1C B1

只要线段A1B1与A B不重合,这就决定C点与C1点不是重合点,且C1点始终保持在切线 L上滑动,这就说明 C1点是圆外点,而C点是圆周上的点,则

∠A C B、∠A C1B都是A B弧对应的角,所以同弧的圆周角大于同弧所对应的周外角,即

∠A C B＞∠A C1B

故有∠A C B＞∠A1C B1结论成立

2)当A B线段平移滑动到其右面A2B2位置时,构成了三角形A2B2C,见图4。

∵∠A C2B=∠A2C B2∠A C B＞∠A C2B

∴∠A C B＞∠A2C B2

根据①和②证明可知,无论在 A B左面平移滑动任意位置A1B1,还是在A B右面平移滑动任意位置A2B2,∠A1C B1、∠A2C B2都分别小于∠A C B,也就是说,A B所处其圆弧位置所对应的∠A C B是最大。

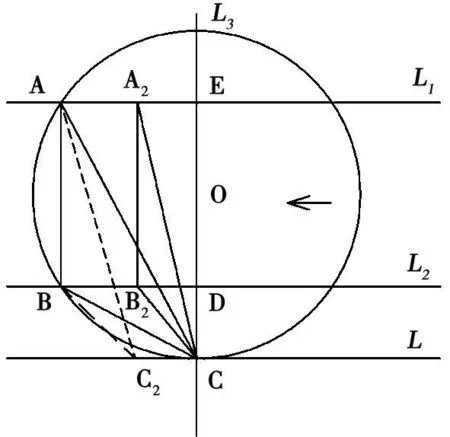
图4 计算简图

3 细线浮标长度公式的推导

设河宽D E=B,仪器所处C点距最近河岸边距离C D= K B,K是C D占河宽D E的比值,细线浮标长度A E=B D=L (严格说是细线在侧向岸边水平投影)(参见图 1)。

∵O E=O D=0.5B 圆半径O C=C D+O D=K B+0.5B

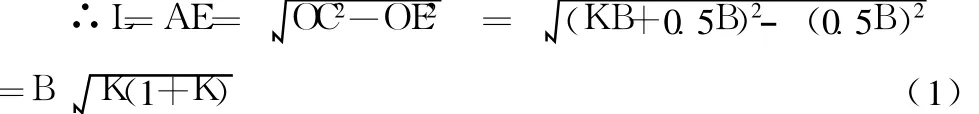
这就是求细线浮标最佳长度的公式。对于不同河宽、不同位置基线的河流断面,其细线浮标最佳长度是不一样的。

强调一点:如果考虑到断面流向偏角 α,可以提前估计一个平均值,就可进一步精确算得细线长度,即 L/C O S α,但一般情况下,断面流向偏角 α很小时,用L就可以满足要求了。

4 结 论

利用细线浮标施测河流流向时,通过最大可视角原理,建立数学模型,并进行了充分论证。根据河流各种断面特点及各种条件,从而可以找到对应的细线浮标的最佳长度。同时,对于普通的浮标测量及其断面设施布设等工作也提供了重要的理论参考。总之,在水利工程测量和水文测验中引用这一设计理念,会使设计更加合理完善、更加科学,对于提高测验成果精度,增强可靠性等,在水文测验中,该设计理念弥补了以往测量方面的不足,具有借鉴性。

[1] 水利部长江水利委员会水文局,中华人民共和国水利部.G B 50179-93河流流量测验规范[S].北京:中国计划出版社出版,1994.

[2] 水利部长江水利委员会水文局,中华人民共和国水利部水文司.S L 58-93水文普通测量规范[S].北京:中国水利水电出版社,1993.