基于双枝模糊逻辑攻击模型的分层推理算法
任大勇
(渭南师范学院,陕西渭南714000)
模糊Petri网作为基于模糊产生式规则知识库系统的良好的建模工具,既结合了Petri网描述异步并发和图形表示的能力,使得知识表示简单清晰.又具有模糊系统的模糊推理能力,便于知识的分析、推理、测试以及决策支持等。但是其缺乏较强的自学习能力,该缺点严重制约了模糊Petri网在各个领域的应用。以模糊Petri网为理论基础的新型网络攻击模型BBFPAN[1],不可避免的也具有自学习能力差的缺点。而对于用于网络系统安全检测和预警的攻击模型来说,具有自学习能力无疑将大大减少其对专家经验的依赖,也将有利于其对网络系统安全漏洞进行实时分析和安全预警。
神经网络(Neural Network)具有很强的自适应和学习能力[2],文献[3-6]将其与模糊Petri网相结合,对模糊Petri网的构建产生积极作用,取得了一定的成果。文献[7]曾通过对没有回路的FPN模型结构进行层次式划分以及建立变迁点燃和模糊推理的近似连续函数,提出了适合模糊Petri网模型自学习的FPN分层算法、模糊推理算法和自学习算法,从而把神经网络中的BP网络算法自然地引入到FPN模型中。但是经实验验证,文献[7]所提出的FPN分层算法并不能对BBFPAN进行很好的分层处理。为了能够将神经网络应用于攻击模型BBFPAN的应用研究中,本文将首先提出一种适合于对攻击模型BBFPAN进行层次式划分的分层算法。
1 分层算法
针对文献[7]中分层算法无法解决攻击模型BBFPAN层次式划分的问题,本文将首先提出一种适用于对攻击模型BBFPAN进行层次式划分的分层算法。在该分层算法中,将把同一个库所的输出变迁尽可能的置于同一层次结构之中,同时在必要时增加相应的虚库所和虚变迁。
在模糊Petri网增加的虚库所和虚变迁只是起到一个中间过渡作用,并不会对模糊规则库系统产生影响,因此也不会改变攻击模型中攻击因素对于攻击效果的作用。按照攻击模型BBFPAN的定义,在分层BBFPAN中,将虚库所对应的θ0设为0,虚变迁的置信度设为1。攻击模型BBFPAN分层算法如算法1所示。
算法1:
Step1:建立起始库所集Pset:若 θi0≠0,则pi∈Pset。设循环变量k,初始值为1,用以标记模型的分层数。
Step2:建立变迁集合:Tk={t∈T|∀p∈◦t,p∈Pset};//Tk表示处于同一层的变迁集合。若T中的变迁t的所有输入库所都属于起始库所集Pset,则将该变迁t置于变迁集合Tk中。
Step3:若 t∈Tk,∃p∈t◦,∃tl∈T-Tk,∃p∈tl◦则,为模型添加虚库所ps和虚变迁tr,其中s =n+1,r=m+1。
t∈◦ps//将变迁t置于新增虚库所ps的输入变迁集中。
ps∈◦tr//将新增虚库所ps作为虚变迁tr的输入库所。
tr∈◦p//新增虚变迁tr的输出库所为库所p。
同时,令:
P=P+{ps},n=n+1;//将新增虚库所ps加入模型库所集P中,n表示库所集P的元素个数。
T=T+{tr},m=m+1;//将新增虚变迁tr加入模型变迁集T中,m表示库所集T的元素个数。
θ0s=0;//新增虚库所ps所对应θs0的设为0。μr=1;//新增虚变迁tr的置信度设为1。
Step4:Pset=Pset∪{p∈t◦|∀t∈Tk};//将Tk中所有变迁的输出库所都添加到起始库所集Pset中。
Step5:T=T-Tk;//从模型变迁集T中删除Tk中的变迁。
Step6:若T=Ø,则算法结束,模型层数为k。否则,k=k+1,转Step2。
2 模糊推理算法
基于双枝模糊逻辑的BBFPAN模糊推理算法是建立在双枝模糊逻辑[8-9]的基础之上的。在该模糊推理算法中,首先以文献[10]中介绍的双枝模糊逻辑推理的几种基本形式为依据,提出BBFPAN模型推理的基本规则。然后,根据BBFPAN模型的基本推理规则,结合BBFPAN分层算法和BBFPAN的定义,给出其相应的分层推理算法。
2.1 BBFPAN基本推理规则
文献[10]中介绍了双枝模糊逻辑推理的几种基本形式,本文在此基础之上,结合BBFPAN的定义提出以下BBFPAN模型推理的基本规则。
与规则,IF d1(θI)and d2(θ2)and...and dn(θn)THEN dg(CF=μ),按照规则中命题(库所)对应网络攻击因素对网络攻击作用的不同,可以将与规则的推理分为以下三种形式:
(1)若θi∈[0,1],i=1,2,...,n,即pi所对应的因素均对网络攻击起促进作用,则
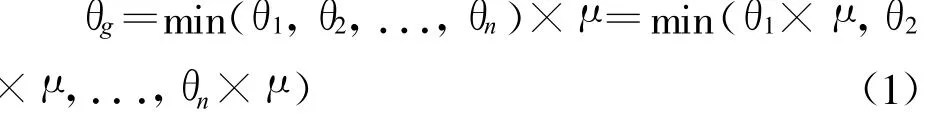
(2)若θi∈[-1,0],i=1,2,...,n,即pi所对应的因素均对网络攻击起抑制作用,则
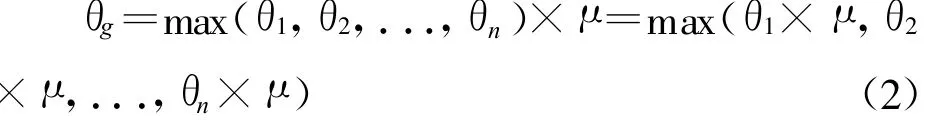
(3)若θi∈[-1,1],i=1,2,...,n,即pi所对应的因素中,既有对网络攻击起促进作用的因素,也有起抑制作用的因素。我们假设:p1,p2,..., pk(1≤k<n)所对应的因素,对网络攻击起促进作用,则θh∈[0,1],h=1,2,...,k;pk+1,pk+2,..., pn所对应的因素,对网络攻击起抑制作用,则θl∈[-1,0],l=k+1,k+2,...,n。那么相应的BBFPAN模型,可以分解为攻击枝BBFPAN和防御枝BBFPAN,如图1所示。
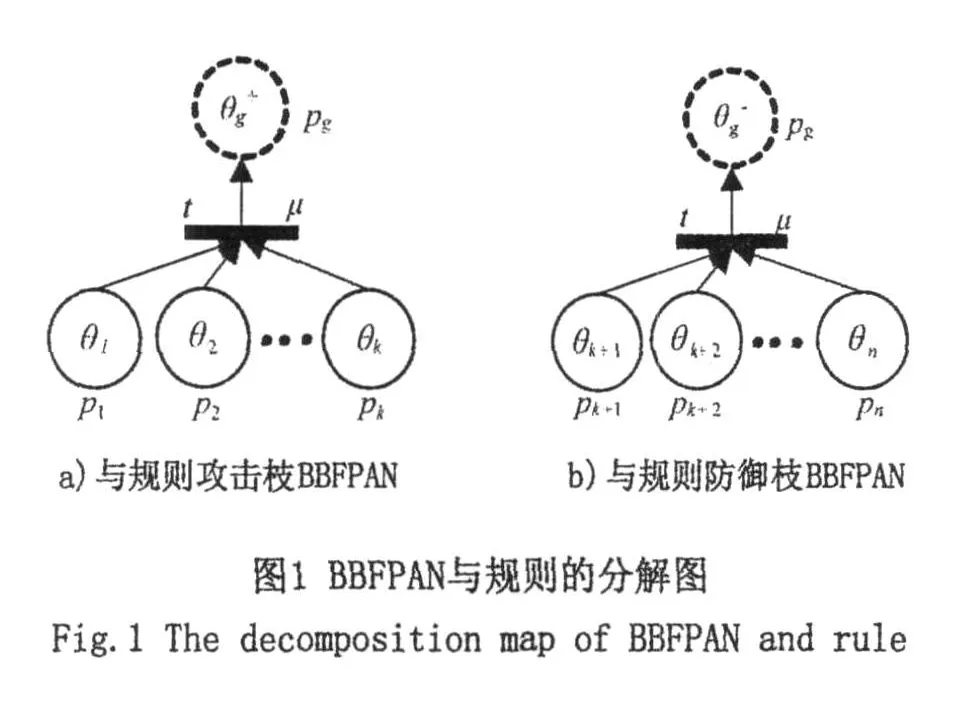

在图1中,我们将 pg库所一分为二,分处攻击枝和防御枝的双枝之上,故而将其表示为虚圈,以示区别。θg+表示了ph(h=1,2,...,k)所对应的对网络攻击起促进作用的因素,对最终状态pg的支持度表示了pl(l=k+1,k+2,...,n)所对应的对网络攻击起抑制作用的因素,对最终状态pg的支持度。
由式(1)和式(2),可以得到

或规则,IF d1(θI)or d2(θ2)or...or dn(θn) THEN dg(CF=μj)j=1,2,...,n,按照规则中命题(库所)对应网络攻击因素对网络攻击作用的不同,也可以将或规则的推理分为以下三种形式:
(1)若θi∈[0,1],i=1,2,...,n,即pi所对应的因素均对网络攻击起促进作用,则
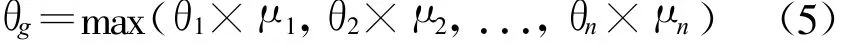
(2)若θi∈[-1,0],i=1,2,...,n,即pi所对应的因素均对网络攻击起抑制作用,则
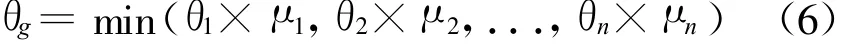
(3)若θi∈[-1,1],i=1,2,...,n,即pi所对应的因素中,既有对网络攻击起促进作用的因素,也有起抑制作用的因素。依照与规则中的假设,可以将相应的BBFPAN模型,分解为攻击枝BBFPAN和防御枝BBFPAN,如2所示。
在图2中,将pg库所采用与图1中相类似的方法,表示为虚圈,以示区别。其中,θg+和所表示的意义与规则中的一致。
由式(5)和(6),可以得到
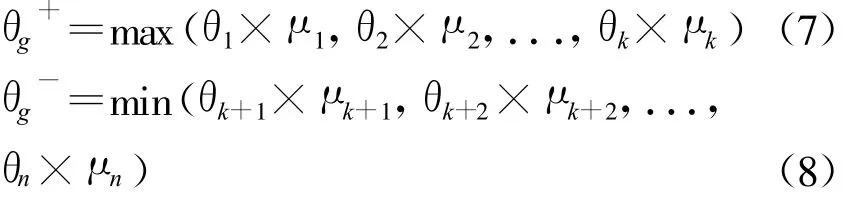
对于与、或两种规则第三种情况下,库所pg的可信度θg,可以分别依据式(3)、式(4)、式(7)、式(8)求得,计算公式为

2.2 分层BBFPAN推理算法
根据以上BBFPAN模型的基本推理规则,结合BBFPAN分层算法和BBFPAN的定义,提出一种分层BBFPAN模型推理的算法。
在该推理算法中,首先根据的 θi0取值情况,构造中间状态库所集Pg,并按照模型的层次结构,逐层对同层变迁集合Tk中变迁tj进行触发。对◦tj按照与规则进行推理计算,并将推理计算结果存放在矩阵θg中。然后,再对中间状态库所集Pg中库所的输入变迁按照或规则进行推理计算,从而得到中间状态库所集Pg中每个库所所对应命题的可信度。分层BBFPAN推理算法如算法2所示。
算法2:
Step1:构造中间状态库所集Pg:若θi0=0,则pi∈Pg。构造矩阵θg={θgij},θgij初值设为0,矩阵θg为n×m阶矩阵。设循环变量l=1;
Step2:∀tj∈Tl,对tj进行如下操作:

boolean flag_pos=false,flag_neg=false;//分别用于标记◦tj中攻击因素的性质


//对◦tj按照与规则进行推理计算,其中 I为变迁tj的输入矩阵,当pi是tj的输入时,I[i][j] =1。
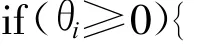
flag_pos=true;//若◦tj中因素对网络攻击起促进作用,则flag_pos为真
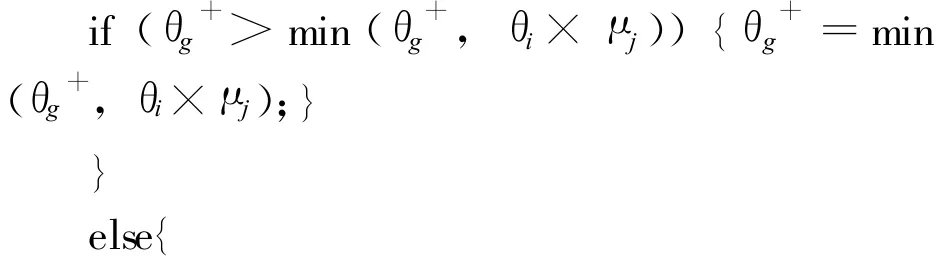
flag_neg=true;//若◦tj中因素对网络攻击起抑制作用,则flag_neg为真
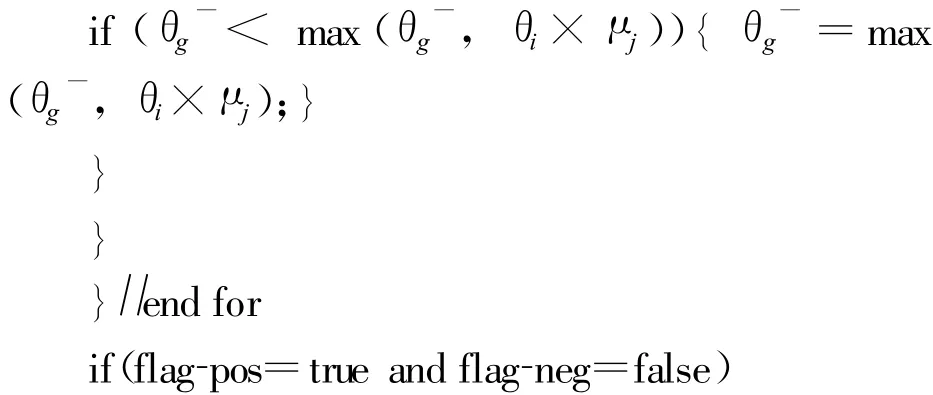
θgj=θg+;tj中仅存在对网络攻击起促进作用的因素。

θgj=θg-+⊕;tj中仅存在对网络攻击起抑制作用的因素。
else θgj=θg+⊕;//否则,根据式(9)求得
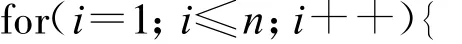
if(O[i][j]==1){//其中O为变迁tj的输出矩阵,当pi是tj的输出时,O[i][j]=1。
θg[i][j]=θgj;//将◦tj中库所对tj◦库所的支持度放入矩阵θg。
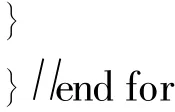
Step3:对∀pi∈Pg,对pi进行如下操作:
boolean flag=false;//用于标记◦pi中变迁是否属于Tl
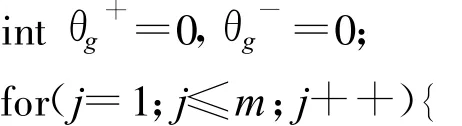


θgi=θg+⊕θg-;//根据式(9)求得θgj。
θi=θgi;//得到库所pi所对应命题的可信度
Pg=Pg-{pi};//从中间状态库所集Pg删除库所pi。
Step4:若循环变量 l=分层层数k,则推理结束;否则,l=l+1,转Step2。
3 实验验证
文献[1]曾以特权提升攻击作为实例,对算法进行验证。本文在此基础之上,构造了一种更为复杂的特权提升BBFPAN模型,分别对BBFPAN分层算法和推理算法进行验证。特权提升分层BBFPAN模型图如图3所示。
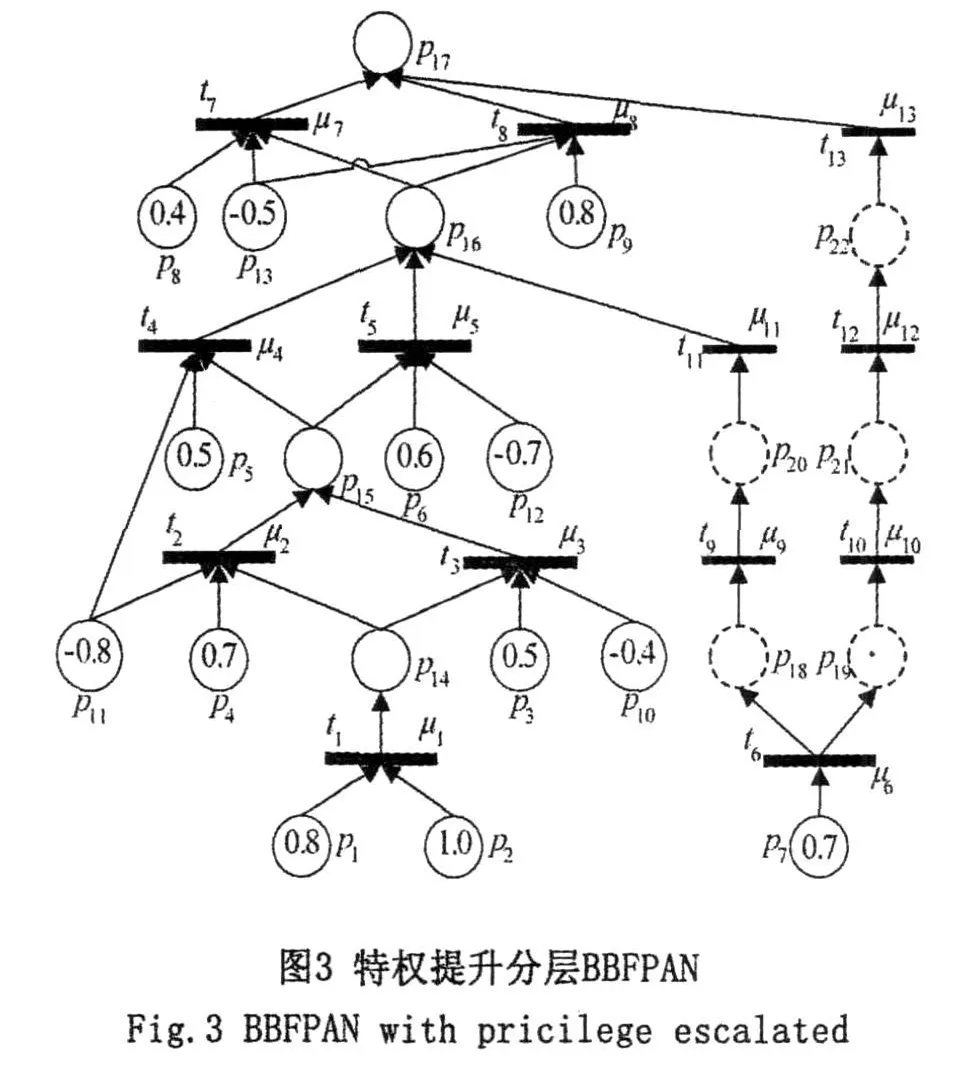

根据图3和BBFPAN的定义,可以得到
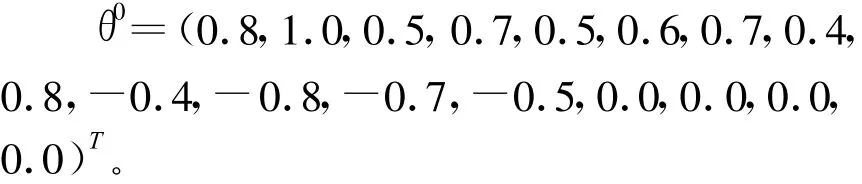
按照算法1第一步的要求可得
模型变迁集 T={t1,t2,t3,t4,t5,t6,t7,t8}。
经过算法1第一轮执行之后T1={t1,t6};
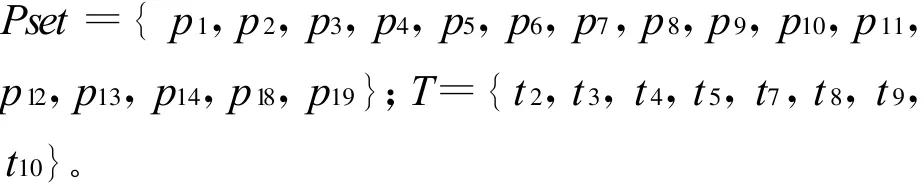
在以上对特权提升BBFPAN分层处理的基础之上,按照算法2即可对特权提升分层BBFPAN中,同层变迁集合T1,T2,T3,T4进行触发推理计算。

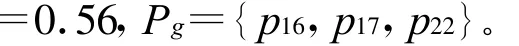
经过算法2第三轮的执行,变迁集合 T3中的变迁将触发,同时可得θ16=0.6,θ22=0.56,Pg= {p17}。
经过算法2第四轮的执行,变迁集合 T4中的变迁将触发,同时可得θ17=0.56,Pg=Ø,算法2结束。
由变迁集合T1,T2,T3,T4可以清晰的看出特权提升BBFPAN变迁触发的层次结构,这说明算法1能够有效的对攻击模型BBFPAN进行分层处理。
由算法2的推理过程,可以看出虚库所和虚变迁在分层BBFPAN中只是起到了相应的过渡作用,并对模型最终推理结果产生影响。节点p7对节点p16的支持度,通过虚库所和虚变迁p18,t9,p20,t11进行了传递;对最终节点p17的支持度,通过虚库所和虚变迁 p19,t10,p21,t12,p22,t13完成了传递。
同时,该BBFPAN分层推理算法能清晰的反映攻击模型中各个节点在不同时刻的状态,从而使模型更加真实直观地反映了网络攻击的演变情况,使我们更好的发现和认识网络系统的漏洞,有针对性地采取相应的安全防御措施。
4 结语
本研究丰富了攻击模型的分析研究方法,同时也扩展了双枝模糊逻辑理论的研究领域。神经网络和新型网络攻击模型BBFPAN的相结合研究,还包括诸如变迁触发连续函数、权值调整等诸多的问题。通过实验验证算法是正确的。
[1]黄光球,任大勇.基于双枝模糊决策和模糊Petri网的攻击模型[J].计算机应用,2007,27(11):2689-2693.
[2]魏海坤.神经网络结构设计的理论与方法[M].北京:国防工业出版社,2005.
[3]FURUHASHI T,YAMAMOTO H.Fuzzy control stability analysis using a generalized fuzzy petri net model[J].Journal of Advanced Computational Intelligence and Intelligent Informatics,1999,3(2):99-105.
[4]宋群,马宏波,王中海.基于NNFPN模型的电梯故障诊断方法的研究[J].控制与决策,2005,20(3):341-344.
[5]胡志刚,马好,廖麟.基于模糊神经Petri网的故障诊断模型[J].小型微型计算机系统,2005,26(11):1978 -1982.
[6]危胜军,胡昌振,孙明谦.基于学习Petri网的网络入侵检测方法[J].北京理工大学学报,2007,27(4):312-317.
[7]鲍培明.基于BP网络的模糊Petri网的学习能力[J].计算机学报,2004,27(5):695-702.
[8]刘刚,徐衍亮,赵建辉,等.双枝模糊逻辑[J].计算机工程与应用,2003,39(30):96-98.
[9]刘刚,刘强.双枝模糊推理框架[J].计算机工程与应用,2004(32):102-105.
[10]刘刚,赵建辉,刘强.双枝模糊逻辑(Ⅱ)[J].计算机工程与应用,2005(19):47-49.

