一种乘同余伪随机序列快速实现的FPGA设计

陈 帅

(淮南师范学院 计算机与信息工程系，安徽 淮南232001)

在扩频通信、信息加密和系统测试等实际应用领域中采用了与随机序列特性类似的伪随机序列[1]。常用的伪随机序列是基于线性反馈移位寄存器的m序列与同余序列(乘同余和线性同余)。

乘同余的随机数发生器[2-3]：y(n+1)=(16807×y(n))mod(231-1)已被广泛应用，其周期为素数231－1＝2 147 483 647=2.147 483 647×109,直接进行该式的乘同余计算需要64位的整数除法运算。最简单的方法是采用循环减法实现该同余序列运算中的整数除法，即采用将积循环减去模数 231-1，直到被减数小于模数231-1，则最后的被减数即为求得的同余数。采用循环相减的方法，若循环的次数多，必然会影响速度。为此，Montgomery[4]提出了一种求两个大整数乘积的模的快速算法，算法不需要除法，只采用乘法、加法和右移位，即采用边乘边移位，其结果还需要进一步处理。如果参加乘积的数很大，则移位很多，必然降低运算速度。参考文献[5]采用改变初始值设定，两次调用该Montgomery算法实现形如 S=(x×y)mod N运算，即两个大整数乘积的模的计算，但运算速度必然又大大降低。

现场可编程门阵列FPGA(Field Programmable Gate Array)编程灵活、修改方便，特别适用于流水线方式与并行方式的数据处理。在很多高速设计和高速测试的场合[6],能够在FPGA中直接实现上述伪随机序列发生器。传统的实现乘同余产生伪随机数的软件方法时钟频率很低，而采用FPGA硬件实现则可以达到更高的速度。本文对该乘同余伪随机序列提出了一种快速方法，该算法特别适合FPGA快速实现。

1 乘同余操作快速算法设计

快速算法流程图如图1所示。算法使用3个32位存储单元，1个32位存储器用于存储常数 16 807，2个32位存储器依次用于存储乘法结果、移位结果、加法结果。此外采用了1个32位的乘法器、2个32位的加法器、少量移位操作和1个最高位分离器。算法步骤如下：

(1)将输入值 y(n)与常数16807分别存入2个 32位存储单元中。

(2)将步骤(1)中数据进行 32位乘法运算,乘积分别存入低32位存储单元和高32位存储单元中。

(3)将乘积的高32位存储单元整体向高位移动1位(将乘积的最高位丢弃)，然后，将乘积的低 32位存储单元的最高位移入乘积高32位存储单元的最低位。

(4)将乘积的低32位存储单元的最高位置为零值；

(5)将步骤(3)、(4)所得的 2个 32位存储单元进行32位的加法运算得到32位的和值。

(6)将步骤(5)所得和值的高位（1或 0值）取出，存入另一32位存储单元，将步骤(5)和值的最高位置为零值(最高位分离)。

(7)将步骤(6)所得 2个 32位存储单元值相加，得到32位的和值，即为乘同余迭代操作计算值 y(n+1)=(16 807×y(n))mod(231-1)。

2 乘同余快速运算的验证

采用FPGA功能仿真验证乘同余的快速算法模型如图2所示。在输入时钟信号clk的上升沿完成对输入信号in[31..0]的一次乘同余计算，产生输出信号out[31..0]， 输出信号为：out[31..0]=(16 807×in[31..0])mod(231-1)，采用Verilog HDL硬件描述语言描述为：

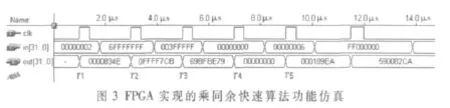
FPGA设计实现的乘同余快速计算的仿真功能如图3所示,T1时刻,输入为0x00000002,在clk的上升沿进行计算：(16 807×2)mode(231-1)=0x834e;T2时刻,输入为0x6fffffff,在 clk的上升沿进行计算：(16 807×0x6fffffff)mode(231-1)=0x0ffff7cb;T3时刻,输入为 0x003fffff,在 clk的上升沿进行计算：(16 807×0x003fffff)mode(231-1)=0x69bfbe79;T4时刻,输入为 0,在 clk的上升沿进行计算：(16 807×0)mode(231-1)=0;T5时刻,输入为 0x00000006,在clk的上升沿进行计算:(16 807×6)mode(231-1)=0x000189ea。可见，FPGA仿真结果与人工计算一致，从而证明了乘同余快速算法的正确性。

2.2 乘同余序列的产生

为了连续产生乘同余序列，需要将上次产生的结果反馈输入作为下次进行乘同余计算的输入值。为此需要对乘同余算法添加选择控制电路，FPGA才能实现序列发生器。设计的电路如图4所示,其中选择控制为快速乘同余计算选择输入的数据，在set=1时完成初始值预置输入，在set=0时进行反馈输入。

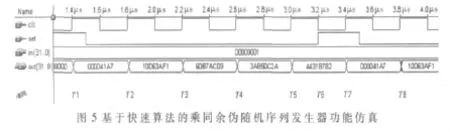
图5为设计的FPGA电路功能仿真图，FPGA采用EPF10K30ATC144-1。在T1时刻以前的set=1预置了初始值0x00000001，从而在T1时刻的时钟clk的上升沿进行乘同余运算得到0x000041A7；在T2时刻的时钟clk的上升沿，由于set=0,将0x000041A7代入进行乘同余运算得到0x10D63AF1；在T3时刻的时钟clk的上升沿，由于set=0,将0x10D63AF1代入进行乘同余运算得到0x60B7ACD9;在T4时刻的时钟clk的上升沿，由于set=0，将0x60B7ACD9代入进行乘同余运算得到0x3AB50C2A；在T5时刻的时钟clk的上升沿,由于set=0,将0x3AB50C2A代入进行乘同余运算得到0x4431B782；在T6时刻开始set=1,故又重新预置初始值0x00000001，然后在T7时刻的时钟clk的上升沿,将0x00000001代入进行乘同余运算得到0x000041A7；在T8时刻的时钟 clk的上升沿，由于 set=0，将0x000041A7代入进行乘同余运算得到0x10D63AF1。

对计算乘同余序列：y(n+1)=(16 807×y(n))mod(231-1)的运算，提出了一种新的快速算法，算法包括1个32位乘法、2个32位加法、少量移位操作和1次最高位分离，不需要除法，只需乘法、加法、移位和最高位分离操作即可。在FPGA上设计了快速同余算法，功能仿真验证了该算法的正确性。

[1]李飞飞,刘伟宁,王艳华.改进的中值滤波算法及其 FPGA快速实现[J].计算机工程,2009,35(14):175-177.

[2]杨波.网络安全理论与应用[M].北京:电子工业出版社,2002.

[3]张传林,林立东.伪-随机数发生器及其应用[J].数值计算与计算机应用,2002,23(3):188-208.

[4]PETER L.Modular multiplication without trial division.Mathematics of Computation,1985,44(170):519-521.

[5]陈政彣.于8051单芯片上实作RSA密码系统之能量击及防御措施[D].台湾：资讯工程研究所,1993.

[6]束礼宝,宋克柱,王砚方.伪随机数发生器的FPGA实现与研究[J].电路与系统学报,2003,8(3):121-124.