圆柱形建筑双幕墙结构的内部风效应

楼文娟，张 敏，2

(1.浙江大学建筑工程学院，杭州310027，louwj@zju.edu.cn;2.桂林理工大学土木工程系，广西桂林541004)

在建筑结构的抗风设计中，设计人员往往把注意力集中在外部风荷载对结构的作用上，而对结构内部风压则关注很少.现行GB50009-2001《建筑结构荷载规范》［1］对体型各异的封闭式建筑的风荷载体型系数作了明确规定，而对结构内部风压仅提供了关于封闭式建筑物的建议，即按外表面风压的正负取-0.2或0.2.而对双层幕墙［2-3］来说，其特点就是在外层幕墙上开有一定面积的永久性通风孔，如图1所示，气流可以通过通风孔作用于内层幕墙，并且气流在双层幕墙之间的通风廊道内形成复杂的流动，因此双幕墙有3个受风表面，即外层幕墙的内、外表面以及内幕墙的外表面，其内幕墙的风压主要由廊道内的风压决定，外幕墙的风载则由外压和廊道内压的共同决定作用，外压的分布主要是由建筑体型决定，这部分的研究较多，荷载规范［1］也做了详细的规定，但廊道内气流的复杂性使得荷载规范规定的建议值远不能满足工程设计的需求，可见了解结构部分开孔时的内部风荷载特性是风工程研究中亟待解决的重要课题.

图1 廊道式通风双幕墙及其纵向剖面图

开孔结构内部风效应研究在国外开展得较早，以Liu和Saathoff［4］为代表的一批学者率先发展了在结构设计中考虑内部风压的方法，从此Woods和Blackmore等［5］学者通过一系列刚性模型风洞试验对结构内部风压进行了细致的研究，关于风致内压静力问题的理论研究也迅速开展起来，1999年Ginger和Letchford［6］进行了足尺房屋墙面开洞时内部风压测定试验，使人们对结构内部风效应有了更深的了解.但这些研究成果基本都是针对大跨屋盖结构的内压，双幕墙结构与大跨屋盖结构的内部流场有很大的不同.国内外关于双幕墙结构风荷载的研究［7-10］只是基于个别的工程项目的试验对双幕墙的风压分布进行了分析，而对影响双幕墙的风荷载分布的因素却鲜有涉及.因此，深入了解双幕墙结构内部风效应的特性并明确其产生机理，并且在理论上得到估算内部风荷载的方法，对于双幕墙结构的抗风设计无疑是非常有意义的.本文针对不同开孔面积及不同廊道间距的双幕墙刚性模型进行风洞试验，研究了风致内压的空间分布规律、廊道内平均风压的产生机理与理论估算问题.

1 模型试验概况

模型原型为直径20 m的圆柱形建筑，圆弧双幕墙的圆心角为120°，内外幕墙的间距分别为0.5 m、1 m和1.5 m，廊道高度为3.6 m.模型几何缩尺比为1:50，在每个楼层的外层幕墙的顶部和底部分别设有出风和进风孔，空气只能通过这些开孔交流，其它地方均密闭.为了得到双幕墙3个受风表面的风压，在模型外幕墙的内、外表面的对应位置分别布置测点，并且在内幕墙外表面的相应位置也布置测点(见图2).在试验时实现了双幕墙3个受风面对应测点的同步测压，以得到内、外幕墙表面的同步风压时程数据.

试验模型如图3所示，监测的双幕墙布置在模型高度的中部.为了模型对比性各高度风速一致，均为9.4 m/s.采样频率273 Hz，采样时间为15 s.每个测点一个工况的风压系数时程样本包含4 096个数据.测压风向角从0～360°，每隔15°为一个工况，风向角定义见图2.考虑到双层幕墙的风压特征与外幕墙开孔率(即开孔面积与外幕墙面积的比值)及廊道间距有关，研究工况如表1所示.

图2 模型平面图、测点布置图及风向角定义

图3 风洞试验模型

表1 风洞试验工况表

在风洞试验中，采取将各测点的压力相对于参考点高度处动压无量纲化的方法，故其风压系数定义为

2 双幕墙廊道内压的空间分布特性

图4是圆弧型双幕墙的内幕墙各测点在全风向角下的风压系数分布图，可以看出，迎风向和侧风向(-90°≤α≤90°)时，廊道内各测点的平均风压系数不一致，而背风向时，其值则非常接近，这主要是迎风向和侧风向时，外幕墙各开孔处的风压不一致，使得廊道内的空气流动非常剧烈，空气流动的过程中与通风孔和廊道内壁产生摩阻损失，导致了其内压不均匀;而背风向时，其外幕墙各孔口处的风压基本相同，使得双幕墙廊道内的空气流动缓慢或不流动，使得压力损失很小，因此，廊道内的压力分布均匀，其值大约等于各孔口风压的平均值.

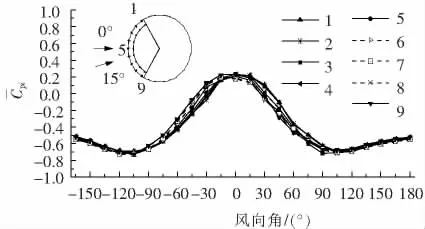
图4 工况4的双幕墙廊道内各测点的平均风压系数

3 双幕墙廊道风压的稳态理论估算

由空气动力学的理论和试验研究成果［11］，孔口两侧的压差与流经该孔的空气流量有如下关系

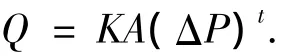
式中:Q为空气体积流量，K为流动系数，与开孔的形状有关，反映了孔口的损失系数，A为开孔面积，ΔP为孔口两侧的压差，t为流动指数，研究［11-12］表明t介于0.5～0.8.

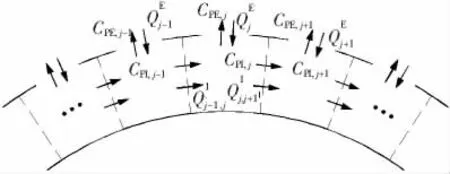
图5 廊道气流和孔口气流示意图

若双幕墙的外幕墙面有n个通风孔，并把双幕墙分隔成n个区域，假定每个区域的内压一致，如图5所示，则第j个通风孔两侧的空气流量为

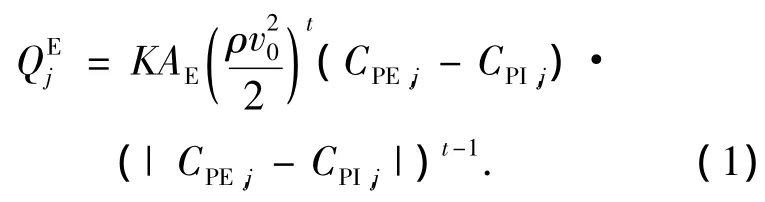
式中:AE为通风孔的开孔面积，CPE，j为第j孔口外表面风压系数，CPI，j为结构廊道内的第j个区域内的风压系数.

由于摩擦阻力的存在，空气在双幕墙廊道内流动，产生压力损失，根据文献［13-14］中达西-威斯巴哈公式可得:其廊道内第j+1区域的空气流入相邻的第j区域的空气流量应为

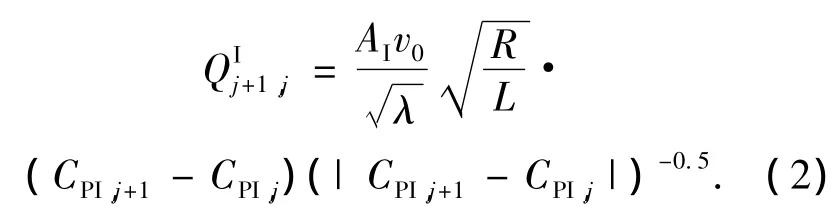
式中:AI相邻两区域的通风孔面积，在此即为双幕墙廊道的横断面面积;λ为沿程摩阻系数，与雷诺数及廊道壁的粗糙系数有关;CPI，j为结构廊道内的第j个区域处的风压系数;R为水力半径，L为空气流经的距离，在此为相邻两分隔区域的中心点间距.

在稳态计算时，考虑空气的不可压缩性，廊道内第j区域的空气流入和流出的流量相等，可得

根据双幕墙廊道内的每个区域的空气流量平衡，可列出n个方程，由于处于圆弧双幕墙端部的两个区域分别只有一个相邻的区域，因此j=1时.将外幕墙各开孔处的孔口平均风压系数CPE，j代入，求解上面这个方程组，就可以得出CPI，j，即廊道内各区域的平均风压系数.

根据本次试验的模型参数，并经过多轮拟合最终确定符合本试验条件状况的参数值，见表2.

表2 各工况下的模型参数

由前面分析已知，30°风向角时外幕墙各孔口处的风压相差较大，180°风向角时其风压则较接近，且篇幅所限，在此就取30°和180°风向角这两个较有代表性的风向角下的各工况的计算结果与试验进行对比验证，如图6所示.从图中可以看出，绝大多数工况的廊道内各测点的平均风压系数与计算值都很较接近，特别是180°风向角时，计算值和试验值几乎一致.

4 影响内压分布的参数探讨

由于K和t均只是反应孔口和廊道的物理环境，在相同孔口条件的前提下，可以讨论其余参量对内压的影响.以下将通过平均内压系数的分析，探讨影响内压的主要因素，为设计提供参考.

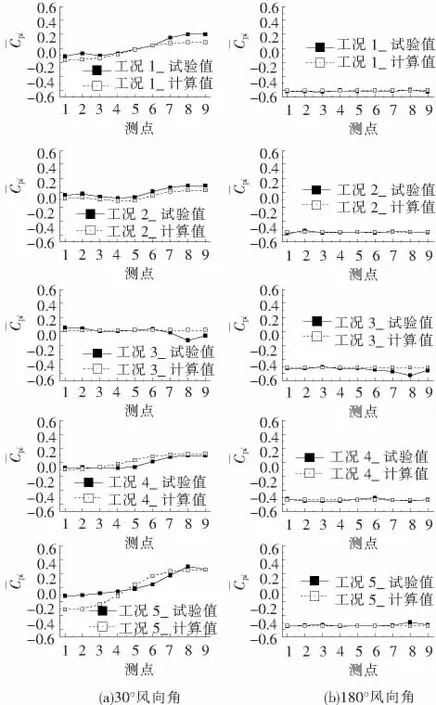
图6 各工况的计算结果与试验对比

4.1 开孔率

此处取5种开孔率(分别为3%、6%、9%、12%、15%)变化为例，图7为圆弧双幕墙的廊道间距为20 mm的工况下外幕墙开孔率变化时的内压变化情况，可以看出:

1)当外压不均匀时，廊道内压随开孔率的增大而变得越来越不均匀，其各测点处的风压越来越接近孔口处的压力;

2)当外压均匀时，廊道内的压力也很均匀，且开孔率的变化对内压的影响很小.

4.2 廊道间距

此处取5种廊道间距(分别为5 mm、10 mm、15 mm、20 mm、25 mm)变化为例，图8为圆弧双幕墙的外幕墙开孔率为9%的工况下廊道间距变化时的内压变化情况，可以看出:

1)当外压不均匀时，同一开孔率的双幕墙，廊道间距越小，其内压受外压的影响越大，就越不均匀;

2)当外压均匀时，廊道内的压力也很均匀，且廊道间距的变化对内压的影响很小.

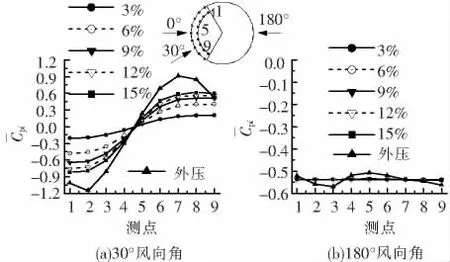
图7 外幕墙开孔率对内压分布的影响

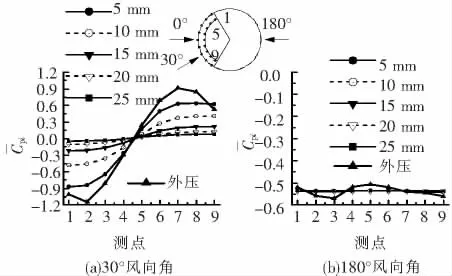
图8 廊道间距对内压分布的影响

4.3 来流风速

此处取5种来流风速(分别为4 m/s、8 m/s、12 m/s、16 m/s、20 m/s)变化为例，图9为圆弧双幕墙的外幕墙开孔率为9%的工况下来流风速变化时的内压变化情况，可以看出:

1)当外压不均匀时，来流风速越大，廊道内气流越剧烈，产生的风压损失越多，廊道内的风压就越不均匀;

2)当外压均匀时，廊道内的压力也很均匀，且来流风速的变化对内压的影响很小.

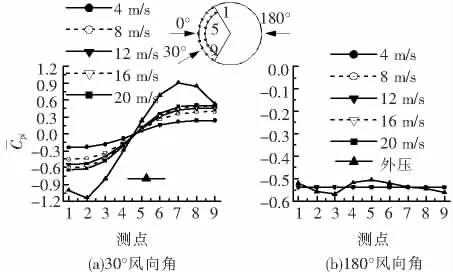
图9 来流风速对内压分布的影响

从以上分析可知:廊道内气流流动是否剧烈是各参数对廊道内压分布影响大小的关键.当圆弧双幕墙的外幕墙各孔口处的风压基本相同时，廊道内的空气流动缓慢或不流动，使得气流与廊道内壁和通风孔摩擦产生的压力损失很小，因此，此时外幕墙开孔率、廊道间距和来流风速的变化对双幕墙平均内压的影响很小，其廊道的内压分布均匀，且大致与孔口处的风压相等.当圆弧双幕墙的外幕墙各孔口处的风压非常不均匀时，压差使得廊道内的空气流动非常剧烈，与通风孔和廊道内壁产生较大的摩阻损失，导致了其内压不均匀;此时空气流动剧烈，因此开孔率、廊道间距和来流风速的大小对风压摩阻损失的影响不一样;开孔率大时，孔口的风压损失小，内压与外压更接近，同时孔口的空气流量大，使得廊道内的空气流动更剧烈，摩阻损失也增大;廊道间距减小时，廊道内空气的摩阻损失增大，使得廊道内的风压更不均匀;来流风速增大使得廊道内的气流流动更加剧烈，增大了摩阻损失，使得廊道内的压力更加不均匀.

图10给出了30°和180°风向角下模型风洞试验的廊道内各测点的风压系数图，可以看出，外压均匀时(180°风向角)，廊道内的风压分布受外幕墙开孔率和廊道间距的影响很小;外压不均匀时(30°风向角)，廊道内风压分布随开孔率的增大和廊道间距的减小越来越不均匀，这与理论分析结果完全吻合，证明前述的理论分析完全正确.

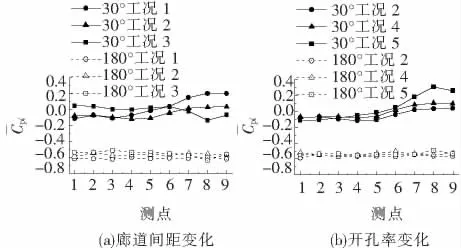
图10 30°和180°风向角下各工况内压分布的对比

5 结论

1)圆弧型双幕墙在迎风向和侧风向时，廊道内的平均风压不均匀，而背风向时，廊道内的平均风压则非常均匀.

2)采用稳态理论估算双幕墙廊道内部各区域的平均风压与试验值吻合较好，当开孔率不是特别小时，其估算值可满足工程精度要求.

3)当外幕墙开孔处的风压均匀时，双幕墙的开孔率和廊道间距的大小及来流风速对其平均内压影响很小，可以忽略.

4)当外幕墙开孔处的风压不均匀时，随外幕墙开孔率的增大、廊道间距减小或来流风速增大，廊道内压变得更加不均匀.

［1］ GB 50009-2001建筑结构荷载规范［S］.北京:中国建筑工业出版社，2002.

［2］ ARONES D.Properties and applications of doubleskin building facades［D］.Cambridge:Massachusetts Institute of Technology，2001.

［3］ KAWAI H.Wind loads on double skin facades with opening windows［C］//Proceedings of the sixth Asia-Pacific Conference on Wind Engineering.Seoul，Korea:［s.n.］，2005:231-247.

［4］ LIU H，SAATHOFF P J.Internal pressure and building safety［J］.Journal of Structural Engineering，1982，108(10):2223-2234.

［5］ WOODS A R，BLACKMORE P A.The effect of dominant openings and porosity on internal pressures［J］. Journal of Wind Engineering and Industrial Aerodynamics，1995，57:167-177.

［6］ GINGER J D，LETCHFORD C W.Net pressures on a low rise full-scale building［J］.Journal of Wind Engineering and Industrial Aerodynamics，1999，83:239 -250.

［7］ 楼文娟，金虎，陈勇，等.双幕墙长矩形建筑风荷载特性的试验研究［J］.建筑结构学报，2005(1):65 -70.

［8］ 楼文娟，李恒，魏开重，等.典型体型高层建筑双层幕墙风荷载特性的试验研究［J］.哈尔滨工业大学学报，2008，40(2):296-301.

［9］ 顾明，黄鹏.双层玻璃幕墙风压分布特性的试验研究［J］.建筑结构，2005(6):68-71.

［10］ DA SILVA F M，GOMES M G，Gap inner pressures in multi-storey double skin facades［J］.Energy and Buildings，2008，40:1553-1559.

［11］ STATHOPOULOS T，KOZUTSKY R.Wind induced internal pressures in buildings［J］.Journal of structural Engineering，1986，112(9):2012-2026.

［12］ 余世策.开孔结构风致内压及其与柔性屋盖的耦合作用［D］.杭州:浙江大学，2006.

［13］ 林建忠，阮晓东，陈邦国，等.流体力学［M］.北京:清华大学出版社，2005.

［14］ 赵学瑞，水力学及空气动力学［M］.上海:上海科学技术出版社，1959.