自混合干涉信号的可变步长LMS滤波处理

王德锋，叶会英

（郑州大学 信 息工程学院， 河南 郑 州 4 50052）

由于激光干涉信号的结构简单、易准直等特点，使得光干涉广泛应用于激光器自身参数和各种高精度的测量。在干涉系统中，外部环境的干扰会影响信号，从而导致采集到的实验数据伴随着大量的干扰和噪声。为提高测量的精度，需对原始数据进行有效的处理，减少各种噪声，提取出有用的干涉信号。结合光反馈信号的特点，在最小均方误差（LMS）算法[1]的基础上，本文提出一种可变步长的LMS算法，该算法实际是在收敛的过程中动态地改变步长。

1 自混合干涉系统的构成及理论模型

光反馈自混合干涉（OFSMI）系统由半导体激光器、透镜和外部反射物体3部分组成，理论模型采用如图1所示的三镜腔F-P等效模型。

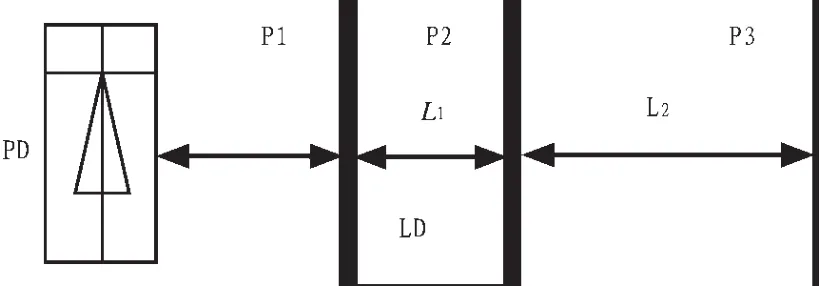
图1 OFSMI系统的三镜腔F-P等效模型

图1中，LD为半导体激光器；L1和L2分别是激光管内腔和外腔长度；P1为激光器前端面；P2为激光器后端面；P3为外部运动物体；PD为封装在激光器内部的光探测器。LD前表面P1辐射光经自聚焦透镜P2照射在被测物体P3上，被散射（或反射）后，一部分光又经原路返回激光器谐振腔，同谐振腔内的原始光相干涉形成新的激光振荡，新的激光波长及功率依赖于反馈光的相位及强度。当被测物体P3沿光轴震动时，输出光功率也随着震动发生变化，由PD监测激光器输出光功率。检测到的自混合干涉信号不仅携载外部物体特性与运动规律等信息，而且携载激光器自身参数的信息。

光反馈自混合干涉系统的数学模型[2-3]表述为：

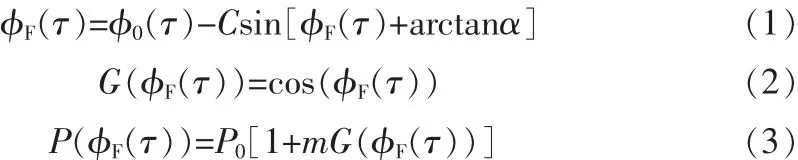
式（1）为激光自混合干涉系统的相位方程。式中，φF（τ）为光反馈存在时外腔的光相位且φF（τ）=ωFτ，φ0（τ）为无光反馈时外腔的光相位且φ0（τ）=ω0τ，其中，ω0和ωF分别为半导体激光器无和有反馈时的角频率[4]；τ=2L/c，其中，L为外腔的长度，c表示真空中的光速；α为线宽展宽因数；C为反馈水平因子。式（2）表述干涉函数G（φF（τ））和含光反馈时外腔相位φF（τ）之间的关系。式（3）是激光自混合干涉系统的功率方程，P（φF（τ））和P0为有外腔和无外腔激光的辐射功率，可看到有外腔激光的辐射能偏离P0为mG（φF（τ）），其中，m为调制系数（典型值为10-3），干涉函数G（φF（τ））表示外腔光相位对辐射功率的影响程度。

2 可变步长的LMS算法原理

自适应滤波因其具有很强的自学习、跟踪能力和算法的简单易实现性，广泛应用于信号去噪领域。当输入过程的统计特性未知时，或输入过程的统计特性变化时，只适应滤波器能够调整自己的参数，以满足某种最佳准则的要求，根据不同的准则，产生许多自适应算法。目前广泛使用的最小均方（Least Mean Square，LMS）算法，是一种用瞬时值估计梯度矢量的方法，该算法的主要特征是低计算量、在平稳环境的收敛性、均值无偏收敛到维纳解等。其原理图[5]如图2所示。

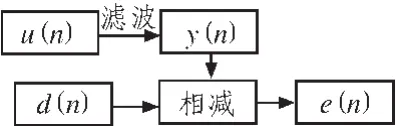
图2 可变步长LMS滤波的原理图

图2中，u（n）是n时刻输入信号，d（n）是期望信号，e（n）是误差，y（n）是滤波器的输出。当u（n）发生变化时，滤波器能够利用变化的误差信号e（n）来调节滤波器自身的参数，从而调节输出。可变步长的LMS迭代公式为：

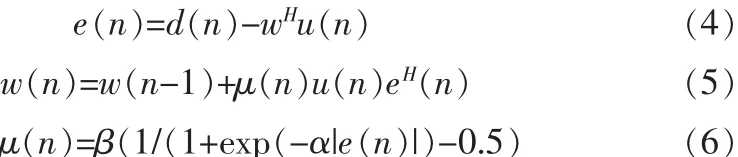
μ（n）[6]是LMS的可变步长，它和误差函数建立起一种非线性的关系，使得步长只与输入的有用目标信号相关，与噪声信号无关，从而降低了算法对噪声的敏感性，并且提高了收敛速度。其中α是控制函数形状的常数；β是控制函数取值范围的常数。

3 可变步长LMS算法的计算机仿真分析

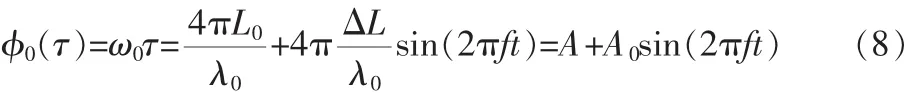
由式（1）～式（3）和式（8）可得到仿真信号。令A=4×105，A0=50，f=195，fs=200 MHz（采样频率），SNR=19 dB（信号与噪声的比）。参数取值为α=2，C=3得到在适度光反馈机制下经LMS滤波后的的干涉信号波形。该算法的流程如图3所示。

由干涉信号式（1）～式（3）的模型可知，通过改变外腔长度L，得到强度函数P随时间变化的信号P（t），这里采用在外腔加正弦波动信号，获得相应的光反馈自混合干涉信号。假定外部物体做简谐运动，其运动规律为：

式中，L0为激光辐射面和外反射体间的初始距离，f为振动频率，t为时间变量，λ0为无光反馈时激光的中心波长。

则不带光反馈时外部光相位为：

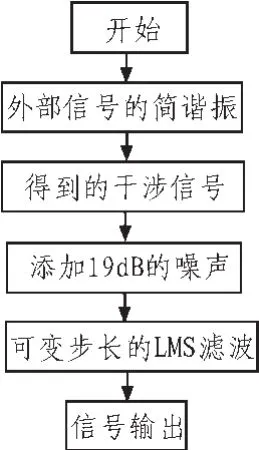
图3 自混合干涉信号可变步长的LMS滤波流程

图4为上述方法经计算机仿真后的归一化效果图。图4中，n为采样点数；G（n）为仿真的干涉信号；GG（n）为加噪声后的干涉信号；out（n）为滤波后的输出信号；e（n）为误差；恢复后信号的均方误差δ=0.004 5，该方法算法简单、运算速度快、有效地滤除信号中的噪声，更适合于在实际测量中应用。

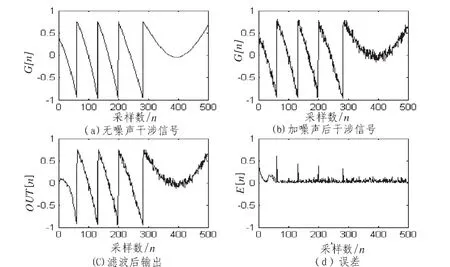
图4适度光反馈（α=2，C=3）

4 结束语

在分析针对自混合干涉信号中噪声和干扰特点的基础上，提出了一种可变步长的LMS自适应算法。将可变步长的LMS算法应用到光干涉的测量之中，从理论上对其分析，并且进行大量计算机仿真，结果表明这种可变步长的算法能够较好地消除干涉信号中的噪声干扰。

[1]张贤达.现代信号处理[M]．2版．北京：清华大学出版社，2002．

[2]Giuliani G，Norgia M，Donati S，et al.Laser diode self-mixing technique for sensing application[J].Journal of Optics，2002，4（6）：283-294．

[3]YU Yan-guang，LI Shi-yang，YE Hui-ying，et al.Estimation for the parameters of semiconductor lasers using the selfmixing effects in semiconductor Lasers[C]//Proceedings of theThirdInternationalSymposiumonInstrumentation Science and Technology，Xi’an，China，2004：665-670．

[4]禹延光，叶会英，姚建铨.多模激光自混合干涉实验与理论分析[J].光电子·激光，2002，13（11）：1190-1193．

[5]刘杰，闫清东.一种新的变步长LMS自适应滤波算法仿真研究[J].微计算机信息，2008（24）：238-239．

[6]张园，王辉.一种改进的变步长LMS自适应滤波算法[J].现代雷达，2008（7）：60-63．