有限微波波束在对称双三棱镜结构中的Goos-Hänchen与 Imbert-Fedorov位移研究

曲敏,黄志洵,逯贵祯

(中国传媒大学信息工程学院,北京 100024)

1 引言

根据理论研究结果表明,全反射条件下线极化电磁波束斜入射到光密媒质与光疏媒质的分界面时,光疏媒质中不仅会形成消失态表面波而且平行于分界面方向能流并不为 0。然而,事实上全反射并没有被破坏,反射能流密度依然等于入射能流密度。鉴于此现象,Picht在 1929年首次提出一个全新的概念[1],全反射无限波束的透射能流由光密媒质进入光疏媒质,然后又返回到光密媒质。这一观点随后被 Schaefer和 Pich在有限宽度波束入射的情况下通过运算论证了[1]。之后,Artmann和 Fragstein都认为这种界面上的能流转移产生了 Goos-Hänchen位移[2]。 1964年,Renard基于 Picht概念和能量守恒定律提出了一种简捷的方法,通过假定部分反射能流与消失态表面波所携带的能流相等来估算 GH位移。

随着光学传感探测技术的不断发展,尤其是位置灵敏探测器(PSD)从一维的发展到多维的,媒质分界面上的波束位移问题重心也从线极化延伸到圆极化。对于圆极化的情况,消失态表面波除了在平行于分界面的平面上有能流,同时在与入射面相垂直的平面上也有能流。也就是在圆极化波入射的全反射中,除了存在一个 GH位移(即纵向位移),全反射波束还会发生一个与 GH位移垂直的位移(即横向位移)。1955年 F.I.Fedorov[3]推想出这一现象,又于 1972年被 C.Imbert[4]实验验证了,故称为Imbert-Fedorov(IF)位移。本文中 GH和 IF位移分别定义为 LGH和 LIF,如图 1所示。值得一提的是,创新性理论与实验表明除 TE和 TM以外的线极化波束也会产生 IF位移[10,11]。

20世纪中叶以来,与消失态表面波相关的界面非几何位移问题引起了大家的极大兴趣。研究范围从单界面[4]到多界面[5,6,7,8,9],使用的结构有介质板结构[5,6]、棱镜 -薄膜耦合结构[7]、以及对称双三棱镜结构[9]等。其中,双棱镜结构在定量研究消失态、分束器设计以及量子势垒等方面有广泛的应用,因此成为理论上和实验上的一个研究热点。本文研究了在对称双棱镜夹层问题中,两块棱镜所夹空气中的消失态能流的分配与分界面上反射波束发生的GH和 IF位移的本质关系。研究从经典电磁理论出发,基于消失态表面波传播特性转变的假设,分析了有限 Gauss平面波束通过对称双三棱镜各分界面时所产生的场分布,因而得出由消失场激发的反射和透射的能流密度。然后通过实验测量验证了假设,并借助 Renard能流法模型推导出针对对称双三棱镜的反射波束 GH和 IF位移表达式。同时,利用数值模拟研究了 GH和 IF位移随夹层间距 d的变化规律,并将其与实验结论对比,结果表明由本文基于实验的理论模型所得的估算式是有效的。

图 1 波束从煤质 n1入射到媒质 n2时反射波束所发生的位移示意图(n1＞n2)

2 双三棱镜对称结构的理论能流模型

由于笔者所在的实验团队已经搭建起微波双三棱镜实验系统,实验中抛物面天线远区一近似平行的波束通过一个带有电大尺寸方孔槽吸波板垂直入射到第一对等边直角三棱镜上,因此在这里我们将针对这一具体的实验设置来提出理论模型。如图 2所示的双三棱镜体系是一种空气夹层结构,两个分界面相互平行。媒质 n1(参数为 n、ε和 μ)与空气的分界面 1位于 z=0,空气层厚度为 d,并在z=d与媒质 n3(参数同媒质 n1)形成分界面 2。θc=arcsin(1/n)＜45°临界角,确保全反射在分界面 1发生。

我们知道,抛物面天线辐射场横截面的振幅分布遵守 Gauss函数,因此这种波场称为 Gauss波束。如果 Gauss波束以 +45°极化入射,则该线极化波可看作为一个 TE极化波与一个等初相、等幅度的 TM极化波的叠加,电场分布表示如下

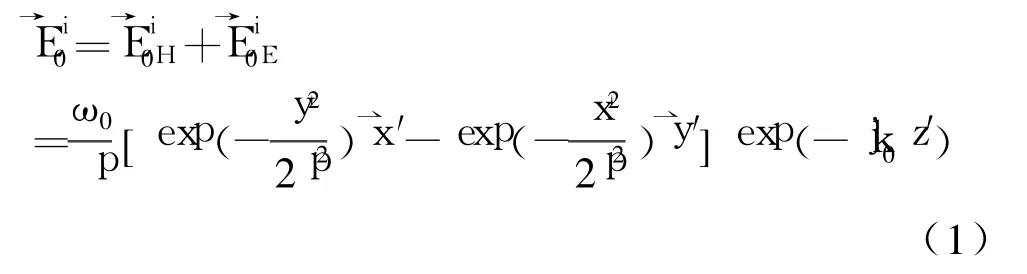
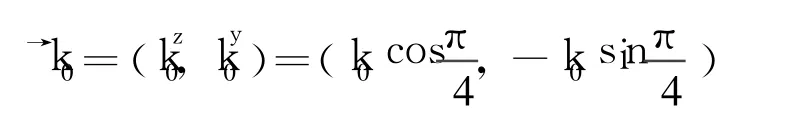
Gauss波束的复半宽度 p

假定 x′y′z′坐标系统的原点为所在直角面的中心点,则媒质 n1与媒质 n2的分界面 z=0上的入射场和反射场分别为

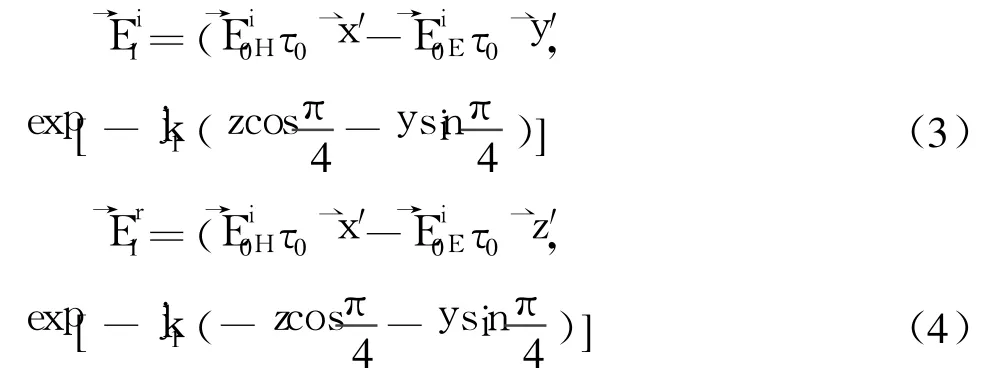
假设不存在媒质 n3,根据经典 Fresnel-Maxwell方程可知从媒质 n1透射到媒质 n2中的消失态表面波场分布[13]为

其中 dp为消失态表面波的穿透深度

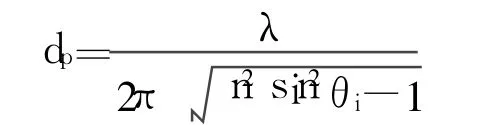
媒质 n2中的波矢量

当加上第二块棱镜 n3,并且 d足够小(根据文献[14]所述,d不能大于透射深度)以致于全反射过程被破坏,也就是形成了受阻全反射(FTIR)结构。假设消失态表面波在媒质 n2与媒质 n3的分界面 z=d上转变成传输波[14],则消失场激发的入射场、反射场为

由波束电场可得到磁场

利用公式(6)(7)(8)可计算 d≤dp时 z=0和 z=d分界面上的反射波束能流密度,即

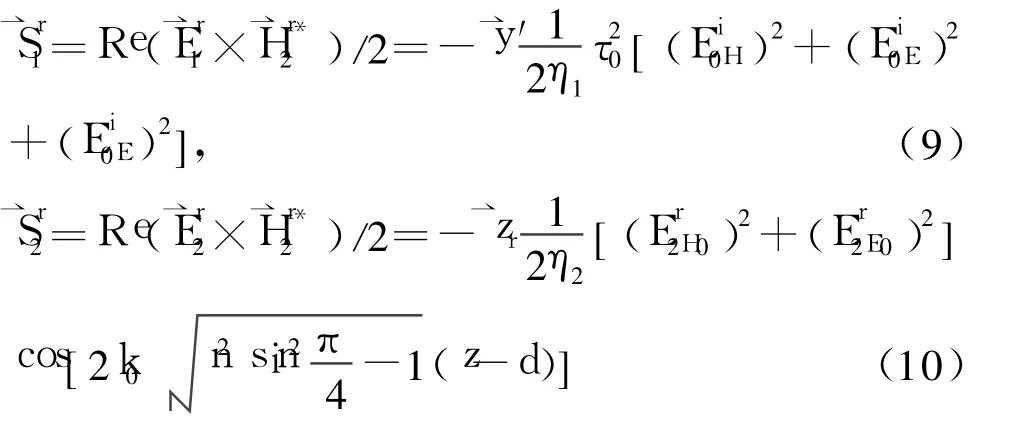
其中 η1和 η2分别为媒质 n1和 n2媒质的波阻抗。

本节基于消失态表面波传播特性转变的假设,认为当发生受阻全反射时媒质媒质 n2中的消失态Poynting矢量流转化成媒质 n1中的部分反射能流和媒质 n3中的透射能流。接下来我们将通过实验测量验证这一假设。

3 基于实验的能流法

为了验证以上的理论能流模型,我们在微波频段改变三棱镜间的空气隙宽度 d来测量双三棱镜实验系统中第一块棱镜的反射功率和第二块棱镜的透射功率,以及第一块棱镜与空气分界面上反射波束发生的 GH和 IF位移,实验系统设置如图 3所示。实验装置的发射部分有 Agilent MXG-N5183A信号发生器,频率范围为 100 KHz～20GHz,最大输出功率为 20 dBm;线极化抛物面发射天线,极化角度可调,直径 200mm。中间被测体由一块带方槽(180×90mm)吸波板和一对有机玻璃三棱镜(320×320×308mm)组成。接收天线为 60×84mm的矩形喇叭;探测设备为 Agilent E4407b频谱分析仪,可精确测量某频率点的功率大小。

图 3 微波双三棱镜实验系统框图

实验对频率为 10.5 GHz的高斯波束通过空气隙为 d(1～35mm)的对称双三棱镜不同路径的传输衰减进行了测量。实验结果如图 4所示,图中红色曲线表明,当 d＜dp时,系统的透射功率随着 d的增大并非指数下降。但是这并不是否认空气隙中消失态表面波的存在,是因为此时消失态能流的一部分返回到第一块棱镜中,另一部分作为透射到第二块棱镜。当 d＜dp时,研究问题就转化为量子隧道效应[15],量子势垒内几率波振幅的变化规律与消失场很像,图 4中的直线就说明这点,并且这时反射波束所携带能流的大小将基本不变,如表 1第二列的后六行所示,因此反射波束的 GH和 IF位移也不改变,大小与对应的单棱镜情况基本相等。

另外,表 1中列出了具体的实验数据,如表 1第五、第六列所示,对称双三棱镜系统中第一块棱镜的反射波束和第二块棱镜的透射波束所携带的能流总量总是与测量时间对应的单三棱镜结构的反射波束能流量相等,并且随着 d的增大,反射能流增大,透射能流减小,两者总量基本保持不变。这是符合Renard能流法中能量守恒这一基本前提的。

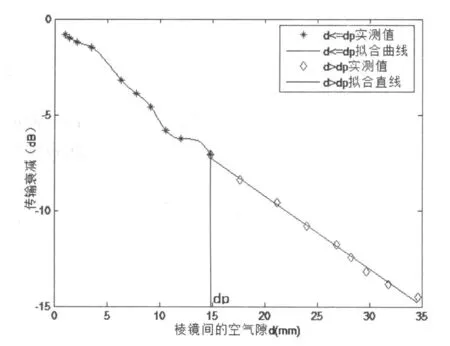
图 4 透射波衰减对间隙d的变化曲线

表 1 双三棱镜结构中的反射与透射功率实验数据(f=10.5GHz,n≈1.48)

由 Renard理论模型[1][12]可知,界面全反射情况下返回到光密媒质中的那部分消失态表面波能量沿 y方向的分量应与光密媒质中的反射波束其中宽度为 LGH那部分能流相等。因此对于双三棱镜的双界面问题可得

将公式(11)、(12)加和,可得到双三棱镜结构中的能流关系,即

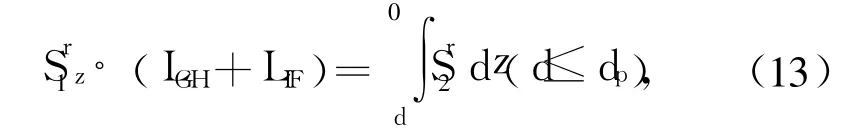
将公式(9)、(10)代入公式(13)可得分界面 z=0上反射波束的位移表达式

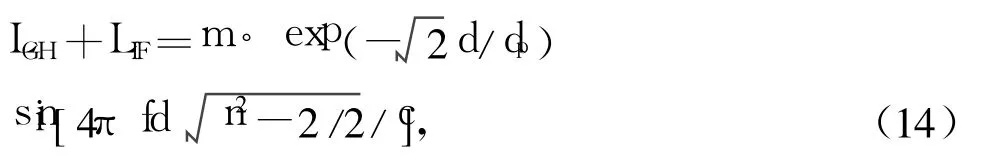
其中常数

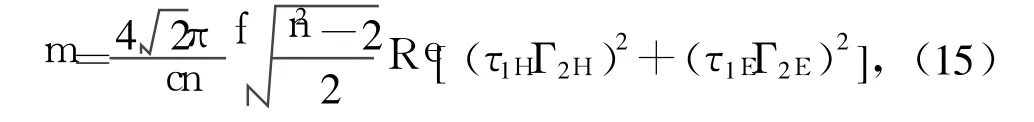
公式(14)就是针对本文实验装置提出的更精确的位移估算式,下面将通过图 5来验证该式的有效性。

4 数值模拟与结论

为了验证公式(14)的有效性,利用了数学软件对其进行数值模拟,并将模拟结果与实验实测值进行比对。

设 f=10.5GHz、n=1.48,则对应的 dp≈14.7mm,m≈5.2。GH和 IF的位移代数和随夹层间距d的变化规律如下图 5所示

如图 5所示实测值与理论值误差小于 5%,理论曲线与实验值拟合曲线都显示了 GH和 IF位移的代数和对间距 d是振荡曲线关系,而且由于空气隙中消失态表面波的传输特性使振荡振幅逐渐减小。因此在一定的误差范围内,可以认为本文理论模型是有效的,同时该理论成果可以指导实验系统误差的改善。

图 5 位移和对间距d的振荡曲线

[1] Rémi H Renard.Total Reflection:A New Evaluation of the Goos-Hänchen Shift[J].Journal of the Optical Society of America,1964,50(10):1190-1197.

[2] Artmann K.Berechnung der Seitenversetzung des totalreflek tierten Strahles[J].Ann Physik,1948,6(2):87-102.

[3] Fedrov F I.Theory of total reflection[J].Dokl Akad Nauk SSSR,1955,105:465-468.

[4] Costade Beauregard O,Imbert C.Quantized Longitudinal and Transverse Shifts Associated with Total Internal Reflection[J].Phys Rev D,1973,7(12):3555-3563.

[5] Tamir T.Nonspecu lar phenomena in beam field reflected bymultilayeredmedia[J].Optical Society of America,1986,3(4):558-565.

[6] Ghatak A K,et al.Beam propagation under frustrated total reflection[J].Optics Communications,1986,56(5):313-317.

[7] Ge Guoku,Li Chunfang,Duan Tao et al.Enhancement of Goos-Hänchen Shift in Prism-Film Coupling Configuration[J].Acta Optica Sinica,2008,28(4):768-772.葛国库,李春芳,段弢,等.棱镜 -薄膜耦合结构中光束 Goos-Hänchen位移的增强[J].光学学报,2008,28(4):768-772.

[8] Cowan J J.Longitudinal and transverse displacements of a bounded microwa-ve beam at total internal reflection[J].JOpt Soc Am,1977,67(10):1307-1314.

[9] Zhu Qibiao,Li Chunfang,Chen Xi.Goos-Hänchen shiftof the transmitted light beam in a two-prism configuration[J].Acta Optica Sinica,2005,25(5):673-677.朱绮彪,李春芳,陈玺.双三棱镜结构中透射光束的古斯 -汉欣位移[J].光学学报,2005,25(5):673-677.

[10] Zhou Huiling,Chen Xi,Li Chunfang.Lateral and Transverse shift of Arbitrarily Polarized Beam in Total Internal Reflection[J].Acta Optica Sinica,2007,26(12):1852-1856.周慧玲,陈玺,李春芳.任意偏振态光束全反射时的侧向和横向位移[J].光学学报,2007,26(12):1852-1856.

[11] Frank Pillon,HervéGilles,Sylvain Girard.Experimental observation of the Imbert-Fedorov transverse displacement after a single total reflection[J].App Opt,2004,43(9):1863-1869.

[12] Thomas Paul,Carsten Rockstuhl,Christoph Menzel,Falk Lederer.Resonance Goos-Hänchen and Imbert-Fedorov Shifts at photonic crystal slabs[J].Phys Rev A,2008,77:(053802)1-7.

[13] Huang Zhixun.Study on the Evanescent State and the Goos-Hänchen Shift[J].Journalof Communication University of China(Science and Technology),2009,16(3):1-14.黄志洵.消失态与 Goos-Hänchen位移研究[J].中国传媒大学学报(自然科学版),2009,16(3):1-14.

[14] Frédérique de Fornel.Evanescent Waves:From Newtonian Optics to Atomic Optics[M].Heidelberg,Springer-Verlag Berlin,2001.

[15] Nimtz G,Stahlhofen A A.How quantum tunneling proceeds faster than light[J].Phy Chem News,2008,39:1-4.