钢管钢骨高强混凝土抗弯构件试验研究

刘 晓，王连广，王 兵

(1.东北大学资源与土木学院，沈阳110004，liuxiao19740701@sina.com;2.沈阳大学建筑工程学院，沈阳110044)

钢管钢骨高强混凝土是将工字钢插入钢管内部，然后灌入高强混凝土的新型组合构件.它比钢管混凝土和钢骨混凝土具有更高的承载能力和抗震延性，并且耐火性和耐腐蚀性能好，施工方便，满足现代工程结构往大跨、高耸、重载和恶劣条件方向发展的要求，具有广阔的市场前景.它所具有的优越性主要是因为3种组合部件的协同工作，首先由于钢管的紧箍作用，提高了核心混凝土的强度和延性;其次钢骨的配置，延缓和阻止了混凝土剪切斜裂纹的产生;最后，混凝土对钢管壁和钢骨的支撑作用增强了局部稳定性，从而有效提高了组合构件的抗压承载力和延性［1-5］.虽然钢管钢骨高强混凝土构件主要应用于承重柱，很少出现纯弯的受力状态，但是为了对压弯、弯剪等受力状态进行深入的研究，对其抗弯性能的研究是十分必要的.目前，国内部分学者对钢管钢骨高强混凝土抗弯性能做了一些研究［6］，为其奠定了理论基础.本文着重研究工字形钢骨的钢管钢骨高强混凝土构件的抗弯力学性能，明确其在弯矩作用下的工作机理和破坏模式，探讨配骨指标和加载方向对其承载力、变形等性能的影响，并在试验分析和理论计算的基础上，根据统一理论给出了钢管钢骨高强混凝土构件抗弯承载力计算公式.

1 试验

1.1 试验参数

本次试验共设计5根抗弯试件，组合截面形式，见图1.截面尺寸D×t(D为钢管外径，t为钢管壁厚)为219 mm×5 mm，试件几何长度L均为1 200 mm，内部分别埋置I10、I12和I14工字钢，钢管内部浇注混凝土为C70.设计配骨指标ρ= (0.3～0.6)，套箍指标θ=(0.73～0.75)，加载方向分别沿工字钢强轴和弱轴，通过钢材和混凝土材料性能试验，得到钢管的屈服强度 fty为350 MPa，混凝土的轴心抗压强度fck为48.6 MPa，其他试验参数和编号见表1.

试件制作时，取长度相同的工字钢和钢管，将钢骨放入钢管中，焊接在同一钢板上.在试件中部的钢管和钢骨同截面粘贴应变片，钢骨的应变片用环氧树脂作防潮处理;混凝土分数次从未焊钢板端浇注，振捣至密实，用高强水泥砂浆找平，养护28 d后，焊接试件上部端板.

1.2 试验方法

试验在500 t压力机上进行，加载方案采用在构件中间直接施加水平力，主要为压弯构件提供理论和试验依据，试验时以钢管下部纤维达到屈服应变时的荷载为正常使用极限荷载，其对应的弯矩为屈服弯矩My，以钢管最大纤维应变εmax达到0.01时的荷载作为极限荷载［7］，其对应的弯矩为极限弯矩Mu.加荷过程中，试件的应变由纵向和横向应变片测得，试件的挠度由竖向布置的位移计测量，试验装置和测点布置，见图1.

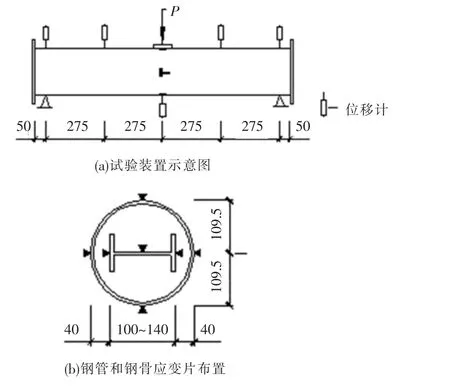
图1 试验装置及测点布置示意图(mm)

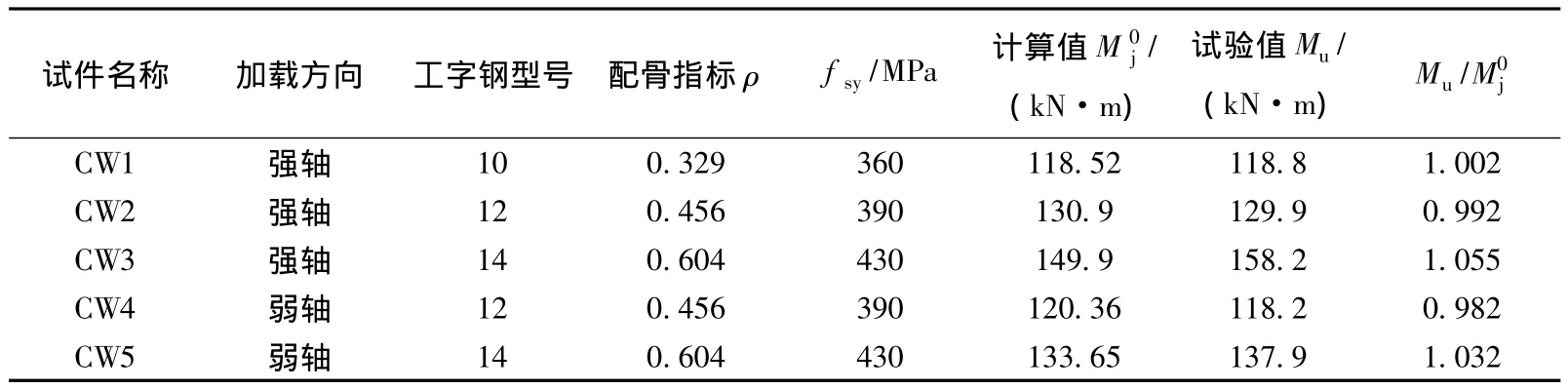
表1 试验参数与计算结果

试验时，采用分级加载制，初期加载每级约为预计极限荷载的1/15～1/12，当加至预计极限荷载的50%时，每级减少到1/25～1/20，持载4 min;大约在80%预计极限荷载时，级差变小，持载2～4 min;在接近极限荷载时，则采取慢速连续加载，当试件的弯曲变形较大时，停止试验.所有测试数据均由UCAM-70A数据采集系统连续采集.

1.3 试验现象

在加载初期，试件挠度变化不大，达到极限荷载的70%之前最大挠度均未超过4 mm，用肉眼基本观察不到，见图2(a);在荷载达到极限荷载的80%左右时，可以观测到试件的受拉区和受压区钢管表面氧化层开始脱落，但没有任何局部的凸曲，表明钢管外边缘纤维已经屈服;在达到极限荷载时，钢管受拉区氧化层脱落较明显，见图2(b);极限承载力后，钢管侧向挠度的增长速度明显加快，进一步增加荷载受压一侧钢管在跨中附近出现局部鼓曲，变形过大停止试验，见图2(c).

图2 试验装置图

2 试验分析

2.1 弯矩－挠度曲线分析

由试验得到各试件弯矩-跨中挠度(M-um)曲线，见图3.主要变化参数为配骨指标和加载方向，它们对弯矩和挠度都有不同程度的影响.

1)不同配骨指标，见图3(a).这3种试件内部分别埋置了I10、I12和I14工字钢，加载方向均为绕强轴方向弯曲，配骨指标ρ增量基本相同，而它们极限弯矩值的增加幅度为=0.219，呈现非线性增长，这是因为它还受内部钢骨配置形式和混凝土的受压区高度的影响;从图3(a)中屈服弯矩My和极限弯矩Mu的相对位置分析，二者的差值随配骨指标ρ的增加而加大，这是因为内部钢骨的不断增加，通过钢管、钢骨和混凝土三者的协同作用，延缓了组合构件破坏速度，改善了内部延性.从图3(a)的跨中挠度(横坐标)分析，可知挠度um随配骨指标ρ的增加而减小，切线模量降低速度随ρ的增加而减缓，说明试件抵抗弯曲变形的能力增强，这是由于内部钢骨面积和惯性矩的增加带来组合试件刚度变大(即EI增加).

2)不同加载方向，见图3(b)(图中标志点为极限弯矩值).这4个试件I12R、I12Q和I14R、I14Q两两之间配骨指标相同，但是相对加载方向的截面布置形式不同，且惯性矩不同，各组增量为ΔI12=441和ΔI14=648，极限弯矩增量为ΔM12= 0.097和ΔM14=0.147 7，二者的比值ΔM/ΔI均为0.000 22，说明极限弯矩值随截面惯性矩成比例增加，钢骨对组合构件的抗弯承载力影响显著，而混凝土和钢管由于受压区面积较小，对抗弯承载力影响相对较弱.从图3(b)横坐标跨中挠度比较分析，内部钢骨相同的强轴和弱轴(即I12R、I12Q和I14R、I14Q)，在极限弯矩处对应的挠度不同，强轴小于弱轴.这是因为内部工字钢强弱轴惯性矩不同，导致试件抗弯刚度EI不同，EI随惯性矩的减小而减弱，进而变形加大.

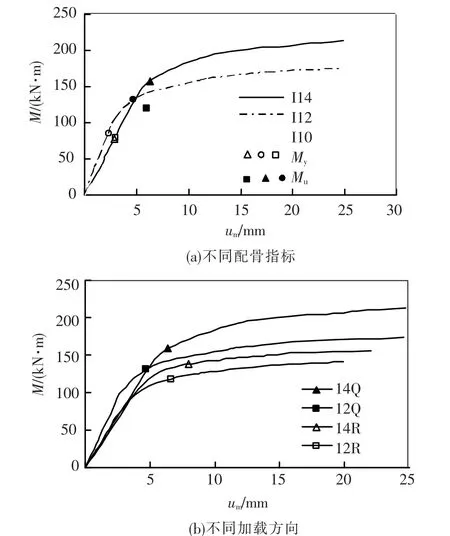
图3 不同参数的弯矩-挠度曲线

2.2 截面应变分布

通过试验得到不同受力阶段钢管外边缘纵向应变沿截面高度变化情况，见图4.

为了更直观地观察两者的变形协调性，将二者应变图形按不同位置叠加，得到图4，在受力初期，钢管和钢骨保持着良好的变形协调关系;随着荷载的增加，压区钢管和钢骨的应变始终保持直线分布，拉区钢管和钢骨的应变则逐渐偏离了直线.但总体看来，仍可近似认为钢管和钢骨变形相协调.

2.3 挠曲变形

由试验得到试件在不同受力阶段的挠度沿长度分布情况，见图5(图中虚线为正弦曲线)，纵坐标为挠度u，横坐标为试件上各点距跨中的距离L.由图可见，此类组合构件屈曲时轴向挠曲变形与正弦半波曲线吻合较好.

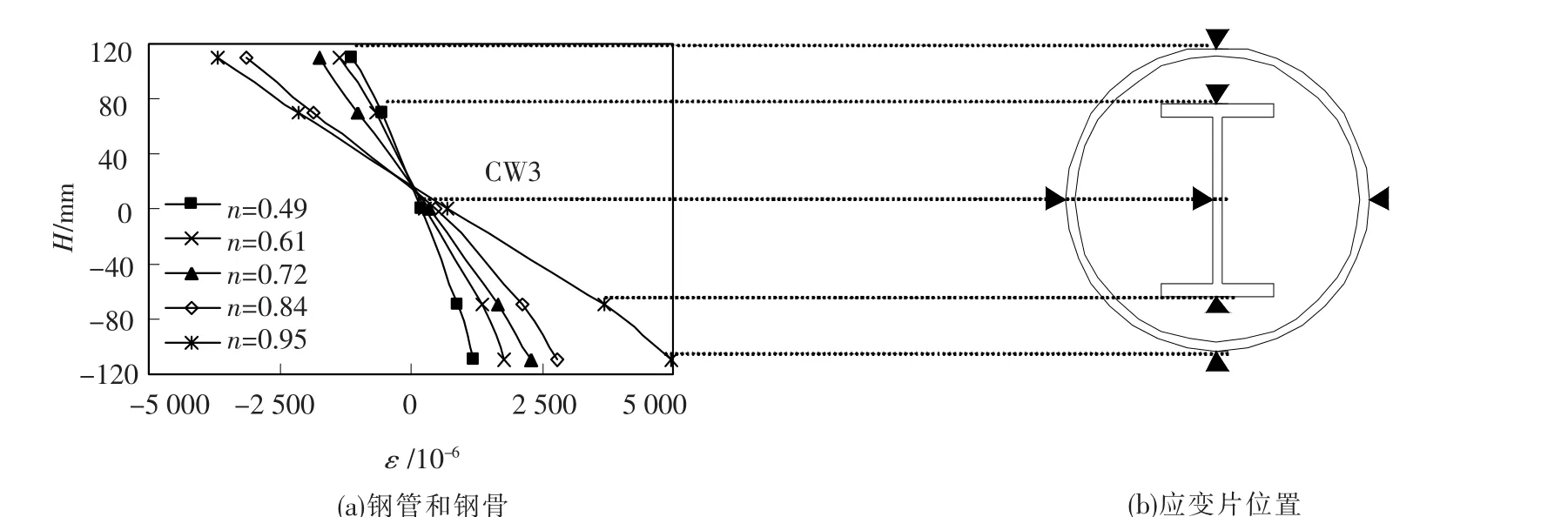
图4 截面应变分布

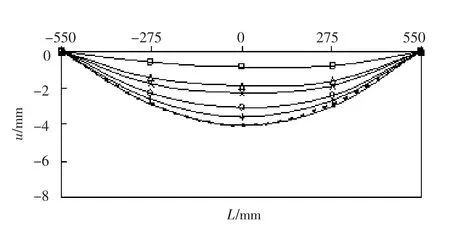
图5 典型挠度曲线

从荷载的增量与挠度变化幅度来看，荷载较小时，竖向挠度变化幅度基本相同，当荷载达到极限荷载的85%时，竖向挠度增长速度逐渐加快，且增加速度与配骨指标ρ成反比，这说明内部钢骨的存在增加组合试件的抗弯刚度，延缓了构件因变形过大而导致的破坏.

2.4 紧箍力分析

钢管混凝土的承载力高于空心钢管是因为内部核心混凝土在钢管的约束下处于三向受力状态，特别是钢管对高强混凝土的约束效应，使混凝土的抗压强度明显提高［8］.紧箍力是由于混凝土的横向变形系数大于钢材的泊松比，在钢管和混凝土的界面间产生，它使混凝土三向受压，钢管双向受力，仍保持弹性工作.本试验通过研究钢管表面的横向和纵向应变比值|εh/εl|与相对弯距(M/Mu)之间的关系，见图6，来分析紧箍力的影响因素.由图可知，受拉区钢管的|εh/εl|均小于0.2，说明受拉区混凝土的横向变形没有超过钢管的横向变形，混凝土处于单向受力状态;受压区钢管的|εh/εl|均大于0.3，说明受压区混凝土的横向变形超过钢管的横向变形，钢管的紧箍作用开始发挥作用，内部混凝土在内外钢材的双向紧箍力作用下处于三向受压状态，当达到极限弯矩的80%左右时混凝土达到极限压应变(图中A点)，体积急剧膨胀，钢管表面的横向和纵向应变比值|εh/εl|明显加大，紧箍作用进一步加强，组合构件承担的荷载仍在上升.

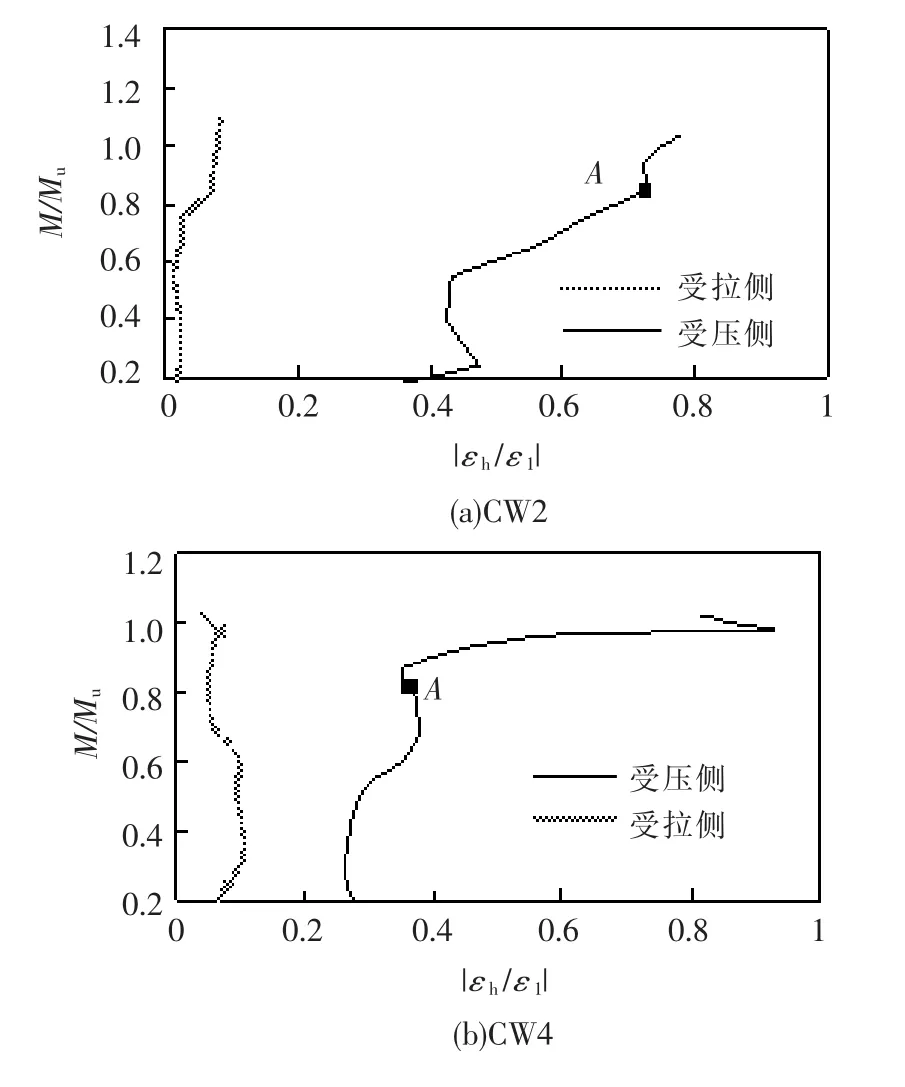
图6 M/Mu相对|εh/εl|曲线

此外，配骨指标和加载方向对紧箍力的发挥作用都有一定的影响:

1)加载方向一定时，配骨指标ρ越大，钢材的纵向变形越小抗弯能力越强，进而使|εh/εl|增加，但紧箍作用发挥不明显;配骨指标ρ较小，钢管表面横向变形速率加快，|εh/εl|增加速度较快，紧箍作用发挥明显.

2)配骨指标一定时，由于强轴方向的抗弯能力强，这使混凝土受压区面积比弱轴大，因此钢管对混凝土的环箍作用发挥显著，即混凝土达到极限压应变之前(A点)受压区钢管的|εh/εl|就大于0.3，见图6(a);而弱轴方向在混凝土达到极限压应变之前(A点)受压区钢管的|εh/εl|在0.3左右，钢管对混凝土的环箍作用发挥不明显，见图6(b);此外，强轴的翼缘与钢管对混凝土形成双重紧箍效应，要强于弱轴的腹板与钢管对混凝土形成的双重紧箍力.

3 承载力计算

根据钢管钢骨高强混凝土的受力特点和破坏机理，结合钢管混凝土和钢骨混凝土抗弯承载力计算方法，本文提出了钢管钢骨高强混凝土抗弯承载力简化计算公式，以钢管混凝土的统一理论为基础，结合钢结构抗弯承载力公式，提出公式的简化形式为

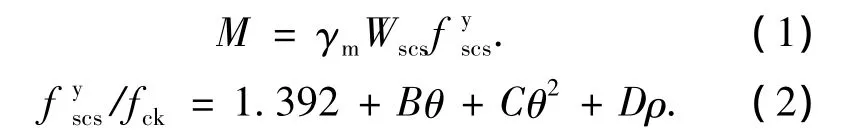
式中:B=0.175 9 fty/235+0.974;C=0.030 9 -0.103 8 fck/20;D=0.156 fsy/235+0.479，γm为截面塑性发展系数;Wscs为钢管钢骨混凝土净截面模量;fy

scs为钢管钢骨混凝土轴心抗压强度.

3.1 截面模量Wscs

截面模量与截面惯性矩有关，圆形截面惯性矩为I=πD4/64;工字钢可通过型钢表或计算得到绕不同轴的惯性矩.则钢管钢骨高强混凝土组合构件的截面模量的计算公式为

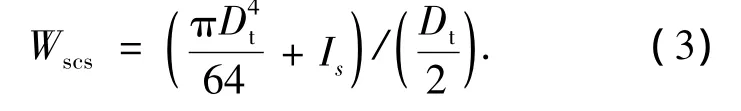
式中:Dt为钢管直径;Is为内部钢骨惯性矩.

3.2 截面塑性发展系数γm

塑性发展系数是考虑构件受力时截面有一定的塑性发展，它等于截面塑性弯矩与截面边缘刚达到屈服应力时的截面弯矩的比值，考虑到截面在受力时不能无限制的应用塑性，所以规范规定对于一定的截面只利用一部分截面塑性，规范对于给定的截面给出了截面塑性系数的值［9］.

考虑钢材强度、混凝土等级、配骨指标和套箍指标，通过计算得到钢管钢骨高强混凝土的抗弯极限值Mu，代入式(1)得γm=Mu/(fyscsWscs)，通过大量数据分析得知，塑性发展系数γm与套箍指标θ、配骨指标ρ以及钢骨与钢管之间的距离有着直接的关系，通过数据回归得到钢管钢骨高强混凝土的塑性发展系数γm，其表达式为

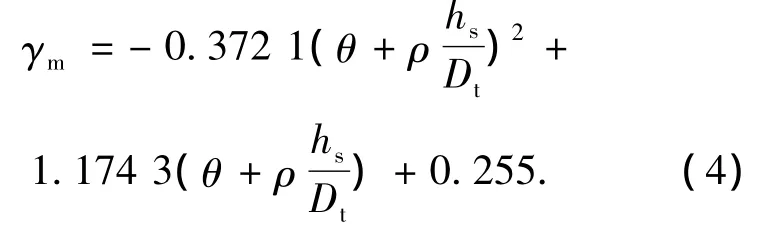
式中:hs为钢骨高度，当弱轴加载时则为翼缘宽度.

将式(2)—(4)代入到式(1)中，即可得钢管钢骨高强混凝土组合构件的简化计算公式.

3.3 公式验证

为了验证钢管钢骨高强混凝土组合构件抗弯承载力计算公式的正确性，将理论计算结果与试验值比较，见表1，其平均误差为1.013，离散系数为0.024，结果非常接近，简单且精确，适合在工程中广泛采用.

4 结论

1)通过5个钢管钢骨高强混凝土构件抗弯承载力的试验研究，可知，钢管钢骨高强混凝土受弯矩作用下，当加载方向一定时，极限弯矩值随配骨指标的增加呈现非线性增长，且变形刚度明显加大，跨中挠度减小;当配骨指标一定时，极限弯矩值随惯性矩的增加基本呈线性增加，跨中挠度弱轴大于强轴.

2)钢管钢骨高强混凝土在整个加载过程中，截面始终保持平面，且组合构件在同一平面内，协同工作;挠度变形曲线符合正弦半波分布.

3)紧箍力沿截面的分布不均匀.在受拉区钢管对混凝土基本没有紧箍效应;在受压区钢管对混凝土的紧箍作用随配骨指标的增加而减小，且强轴的紧箍效应要比弱轴明显.

4)建立了钢管钢骨高强混凝土抗弯构件的承载力计算公式，理论计算结果与试验结果吻合很好，但是公式适用性还需要试验进一步验证.

［1］韩林海.钢管混凝土结构——理论与实践［M］.2版.北京:科学出版社，2007.

［2］BRUNEAU M，AND MARSON J.Seismic design of concrete-filled circular steel bridge piers［J］.Journal of Bridge Engineering，2004，9(1):24-34.

［3］叶列平，方鄂华.钢骨混凝土构件的受力性能研究综述［J］.建筑科学，2000，33(5):1-12.

［4］王连广，李立新.国外型钢混凝土(SRC)结构设计规范基础介绍［J］.建筑结构，2001，31(2)，23-24.

［5］European Committee for Standardization.Eurocode 4:design of composite steel and concrete structures［M］.London:British Standard Institution，1994.

［6］赵大洲，王清湘.钢骨-钢管混凝土组合柱承载力分析［D］.大连:大连理工大学，2003.

［7］蔡绍怀.现代钢管混凝土结构［M］.北京:人民交通出版社，2003.

［8］刘界鹏，张素梅，郭兰慧.圆钢管约束高强混凝土短柱的轴压力学性能［J］.哈尔滨工业大学学报，2008，40(4):528-531.

［9］中华人民共和国建设部.GB 50017—2003.钢结构设计规范［S］.北京:中国计划出版社，2003.