基于两阶段集成学习的分类器集成

李文斌,刘椿年,钟 宁,3

(1.石家庄经济学院信息工程学院,石家庄 050031;2.北京工业大学电子信息与控制工程学院,北京 100124;3.日本前桥工业大学生命科学与信息学院,群马 371-0816,日本;4.河北师范大学 软件学院,石家庄 050016)

集成学习主要通过决策优化或覆盖优化 2种手段将若干弱分类器的能力进行综合,以优化分类系统的总体性能[1].近年来,多分类器集成已成为研究者们关注的一个热点[2-8].集成学习的研究被认为是当前机器学习的四大研究方向之首[9].训练多个个体学习器是集成学习的第 1步,集成则是将这些个体学习器进行组合.文献[10]中,按照个体学习器生成方式的不同,将集成方法大致分为 2类:以 AdaBoost为代表的提升(Boosting)方法(统称该类为 Boosting);另一类以装袋(Bagging)为代表(统称这一类为Bagging).

本文提出了 1种介于 Bagging和 Boosting之间的集成学习方法,称为两阶段集成学习(two-phase ensemble learning,简称为 TPEL).TPEL包括 2个过程:直接学习和间接学习.直接学习指从给定的训练例中学习出多个个体分类器的过程;间接学习则指从这些个体学习器拥有的“知识”中学习集成分类器的过程.结合电子邮件过滤这样1个 2类文本分类问题[11],本文设计并实现了一系列实验,实验中采用朴素贝叶斯方法(Na·l·ve Bayes,简称为 NB)为基线分类器(baseline classifier),其判别函数参见文献[12].对邮件过滤而言,误拒和误收错误的代价是不同的[2],本文仅将邮件过滤看作是普通的2类文本分类问题加以研究,未考虑邮件过滤的特殊性.

1 两阶段集成学习(TPEL)

Bagging[13]和 Boosting[14]是 2种有代表性的集成学习方法,TPEL的设计来自于对 Bagging和 Boosting的分析.

1.1 Bagging及 Boosting分析

对 2类分类问题而言,Bagging学习的预测函数 H可以表示为

其中,x是新例;c0和 c1是类别标识符;L是弱学习算法;T是训练轮数;Li是第 i轮学习出来的分类器.当Li认为 x是 c1类别时,Li(x)输出 c1,否则输出 c0.

Boosting算法最早可以追溯到 1990年,由 Schapire[14]提出.Freund[15]于 1995年提出了 AdaBoost算法.就 2类分类问题而言,K可以表示为

其中,x是新样本,wi是第 i(i=1,…,T)个预测函数 Li的权重(通常在训练例上分类效果越好的预测函数,它的权重越大,相反则越小).

本文中 H和K为集成函数,统一记为 E.从上面的描述可知,Bagging和 Boosting的集成函数都被事先设定了类型或形式.Bagging的集成函数 H是 1个分段函数,Boosting的集成函数K是 1个线性组合函数.若令 y=〈L1(x),L2(x),…LT(x)〉,当 x变化时,y在T维空间形成了一系列点,一部分点的真实类别为c1,记为 Y1;另一部分点的真实类别为 c0,记为 Y0.Bagging和 Boosting则假定了 1个超平面,将这 2类点分开,图 1以 Bagging为例进行说明.图 1中,立方体的每个顶点代表 1个 y向量,圆形所示的顶点是Bagging标注为 c1的点.Bagging假定 A、B、C这 3个顶点决定的面是将 Y1和 Y0分开的分类超平面,该平面上及其法线方向的上方区域被 Bagging认为是 Y1中的点所在的区域,该平面法线反方向所指的下方区域被认为是 Y0中的点所在的区域.

显然,事先设定将 Y1和 Y0分开的分类超平面的办法将导致算法的性能不确定.事实上,正是这种对集成函数的预先设定,导致了 Bagging和 Boosting的一些缺点和现象:

1)Bagging能提高不稳定学习算法的预测精度,而对稳定学习算法效果不明显,有时甚至使预测精度降低[13].

2)Boosting和 Bagging的轮数并非越多越好[16].

3)Boosting方法在有效时效果比 Bagging还好,但在无效时却可能使学习系统的性能恶化[16].

为此,在 TPEL中采用学习算法学习将 Y1和 Y0分开的分类超平面,即 TPEL采用学习的办法对集成函数进行构造.

1.2 TPEL算法

TPEL包括 2个阶段:直接学习和间接学习.TPEL直接学习的学习任务是利用 1个或多个同构或异构的学习算法从训练集中学习多个个体分类器,设为 fi(i=1,…,m).对 2类分类任务而言,个体分类器可表示为

式中,R为分类器输出的类别概率;x是 1个文本向量;d是 x的维数.间接学习则指从个体分类器拥有的知识中进行学习的过程.

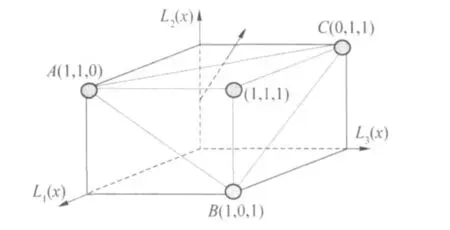
图 1 Bagging假定集成函数形式的示意图Fig.1 Illustrative figure of Bagging's predefined ensemble function

显然,TPEL的关键问题是如何表示个体分类器的知识,下面给出本文采用的 1种知识的表示方法.设 D是训练集,其中有 ｜D｜个样本,它们的期望输出为

式中 yi(i=1,…,｜D｜)表示第 i个样本的期望输出,yi∈ {c0,c1}.

设 Yk(k=1,…,m)是个体分类器 fk在 D上的实际输出,Yk=[yk1,…,yk｜D｜]T,ykj是 fk对第 j(j=1,…,｜D｜)个训练例的实际输出.由于某些 fk输出的是类别,此时 ykj∈{c0,c1};某些 fk输出的是函数值或概率值,此时 ykj∈R.个体学习器拥有的知识被表示成矩阵K的第 i行 ki代表第i个训练例 xi(i=1,…,｜D｜),ki的第 j个单元 kij的值代表了 fj对 xi的分类知识(j=1,…,m),ki(m+1)则指示了 xi的期望类别.从而,对 2类分类问题而言,间接学习的任务是学习分类超平面(即集成函数 E),将K中 c1类别和 c0类别的样本在空间中分开.

前文中,Bagging和 Boosting的集成函数都被事先假定了类型或形式,而 TPEL中的集成函数则是通过间接学习中采用的学习算法而得.因此,TPEL具有更强的泛化能力及鲁棒性,这一点在实验中得到了很好的验证.

算法 1和算法 2分别给出了为 2类文本分类设计的 TPEL的训练和分类算法.

算法 1TPEL-trainer(D,L[1..T],L0,T) ∥L[1],…,L[T]是学习算法

输入:训练集 D;轮数 T;T个学习算法 L[1],…,L[T];集成函数学习算法 L0

输出:T个分类器:f1,…,fT;集成函数 E

从算法 1可知,TPEL要进行 2次分类器的训练,第 1次是训练 T个个体分类器(算法 1的#1行),第 2次是从 T个个体分类器的知识矩阵中训练得到集成函数(算法 1的#2～4行).这 2次训练似乎使 TPEL需要很长的训练时间,但实际情况并非如此.首先,f1,…,fT的训练过程是互不相干的,因此,各模型的训练可“并发”执行,所需的时间仅比训练单分类器的时间稍长.在这点上,与 Bagging方法相同.Bagging类方法随机选取训练子集训练个体学习器,由于各训练子集间相互独立,使 Bagging的各个预测函数可并行或并发生成.其次,K的纵向维数 T通常非常小,因此算法 1中#4行的学习过程所花费的时间非常少,上述 2点在实验中都得到了验证.值得指出的是:算法 1的#3.2行对K中相应单元赋值为类别值,在实际使用中,可以是弱分类器对当前样本输出的类别概率或函数值.

算法 2TPEL-classifier(x,P,f1,…,fT,E)

输入:新邮件 x;P的默认值为 T;T个个体分类器为 f1,…,fT;集成函数为 E;

输出:c0或 c1

IF(至少 P个分类器认为 x是 ci)THEN RETURN ci∥i=0或 1,P由用户设定

从算法 2可知,TPEL与 Bagging、Boosting类算法对新样本的分类有明显区别.当新样本到达时,Bagging首先利用 T个个体学习器产生向量 X=〈m1,…,mT〉,其中 mj(j=1,…,T)是第 j个分类器对新样本的标注结果,然后根据X输出多数分类器赞成的标注结果.Boosting类的算法则根据各弱分类器的标注决定新样本的最终类别.TPEL则是将各分类器的实际输出向量 X=〈m1,…,mT〉作为集成函数的输入,由集成函数决定新样本的类别.TPEL的集成函数是根据分类器在训练例上的分类历史学习得到的,一方面,当训练例发生变化时,重新训练可使集成函数发生相应改变;另一方面,改变间接学习过程中的学习算法也可使集成函数发生变化.这就意味着,TPEL的集成函数将会根据实际情况“动态”地决定 X的最终类别,这样的做法将使结果更加可靠.

设有 3个弱分类器 M1、M2、M3,3个训练样本 x1、x2、x3,它们的真实类别分别为 0、0、1.另设有新样本x4,其期望类别是 0.这 3个弱分类器对 x1、x2、x3的输出向量分别是 〈1,1,0〉、〈1,1,0〉、〈0,0,0〉,在 x4上的实际输出向量为〈1,1,0〉.Bagging认为,x4的类别是 1.然而,当弱分类器的输出向量为〈1,1,0〉时,在训练例上的真实类别总是 0(如:x1、x2),而不是 1.因此,如果 Bagging能了解这一点,就不会对 x4的类别判定犯错误.然而,TPEL利用弱分类器在训练例上的分类“知识”能发现这一点,从而输出 0为 x4的真实类别.也就是说,Bagging类的方法并不根据弱分类器对训练例的分类情况输出新样本的类别.尽管Boosting算法考虑了弱分类器对训练例的分类情况,但最终的投票函数形式过于单一化.

2 实验

本文实验验证了以下问题:

1)弱学习器的个数对 TPEL预测效果的影响;

2)弱学习算法的类型(同构或异构)对 TPEL预测效果的影响.从第 2节可知,Bagging、Boosting类方法通常只可以集成多个同构的弱分类器(实际上,Bagging可集成异构的);而 TPEL可集成多个同构或异构的分类器.

3)弱学习算法的稳定性对 TPEL预测效果的影响.学习算法的稳定性是指当训练集发生较小变化时,学习结果不会发生较大变化.文献[12]指出,稳定性是影响 Bagging预测效果的关键因素.对不稳定学习算法(如:决策树和神经网络),Bagging能提高它们的预测精度,而对稳定的学习算法(如:k-NN、NB),Bagging的效果不明显,有时甚至使预测精度降低.

4)TPEL的时间复杂度.

实验的硬件环境为:IBM T42笔记本(CPU:2.0 GHz;内存:512 M);软件环境为:JBuilder X+Weka[17]开发包.除特别说明,分类器参数都使用 Weka的默认参数.

2.1 实验数据集及评价指标

本文采用了 4个公用的电子邮件测试集,分别是 PU1[18](下文用 D1表示),Lingspam[19](用 D2表示),Spam Assassin[20](用 D3表示),Spambase[21](用 D4表示).这 4个数据集中,2类(垃圾邮件和正常邮件)文本的数据分布情况见表 1.

表 1 实验数据分布情况Table 1 Experimental data distribution

对文本分类任务而言,常用的评价指标为查准率(precision,简写为 p)、查全率(recall,简写为 r)及F1值,计算公式见文献[22].本文实验中采用的测试方法均为开放测试(数据集中 66%作训练,34%作测试);特征提取算法为信息增益(information gain,简称为 IG)[22],特征子集的大小为 150;文本表示的方法为二进制词频.Spambase数据集中的每个邮件文本在发布时已经被表示成了向量形式,所以对这一数据集未做特征子集提取,表示的方式上也未做额外的处理.

2.2 实验结果

实验 1基准结果(baseline results).表 2给出了 NB、Bagging、AdaBoostM1这 3种方法在 4个数据集上的结果,其他实验将与此作参考进行分析比较.表中,p(i)、r(i)、F1(i)(i=0,1)分别表示 p(ci),r(ci)和 F1(ci);P表示总的正确率(为正确分类的测试样本数除以总测试样本数).从表 2可以看出,若仅根据P判断,Bagging在 D1、D2上的性能差于 NB;在 D 3、D4上要好于 NB,尤其是在 D4上.AdaBoostM1在 D1、D2、D3上要好于 NB,在 D4上与 NB的效果一致.

表 2 NB、Bagging和 AdaBoostM 1在 4个数据集上的实验结果Tab le 2 The experimental resu lts of NB,Bagging and AddBoostM 1 on four datasets %

实验 2弱分类器个数对 TPEL性能的影响实验.本实验分为以下子实验:

1)第 1阶段分别采用 5、20、50、100个 NB学习器,第 2阶段采用 NB学习器;

2)第 1阶段分别采用 5、20、50、100个径向基网络(RBFNetwork,简称为 RBF)学习器,第 2阶段采用RBF学习器.

3)第 1阶段分别采用 5、20、50、100个 J48学习器,第 2阶段采用 J48学习器.

4)第 1阶段分别采用 5、20、50、100个 PART学习器,第 2阶段采用 PART学习器.

上述 4个子实验的结果如图 2所示.

由图 2(a)可知,当弱学习器个数 T发生变化时,在前 3个数据集上,P基本不变;在第 4个数据集上,当 T取 100时,P值微弱变小.从图 2(b)来看,在 D1和 D2两个数据集上,仅当 T取 50时,发生了变化,T取 5、50、100时,P基本不变.在 D3、D4上,当 T从 5变化到 50时,P呈增加趋势,当 T变化到 100时,D3上的 P基本不变,而 D4上的 P值有所下降.图 2(c)显示的变化最为无序,但整体上来讲,当 T改变时,P的变化幅度都不大,在 D1上的变化区间为[94.61%,95.96%],D2上的变化区间为[97.87%,98.17%],D3上的变化区间为[97.56%,98.39%],D4上的变化区间为[94.25%,95.27%].图 2(d)表明,当 T从5增加到 100时,在 4个数据集上,P值都呈不断增加的趋势.

总体来看,该实验的结果表明,在4个数据集上,当T变化时,TPEL在P上的变化幅度都不大.从图 2来看,T取 50时,P在 4个数据集上都有较好的表现,因此,在实践中,建议 T的值不超过 50.

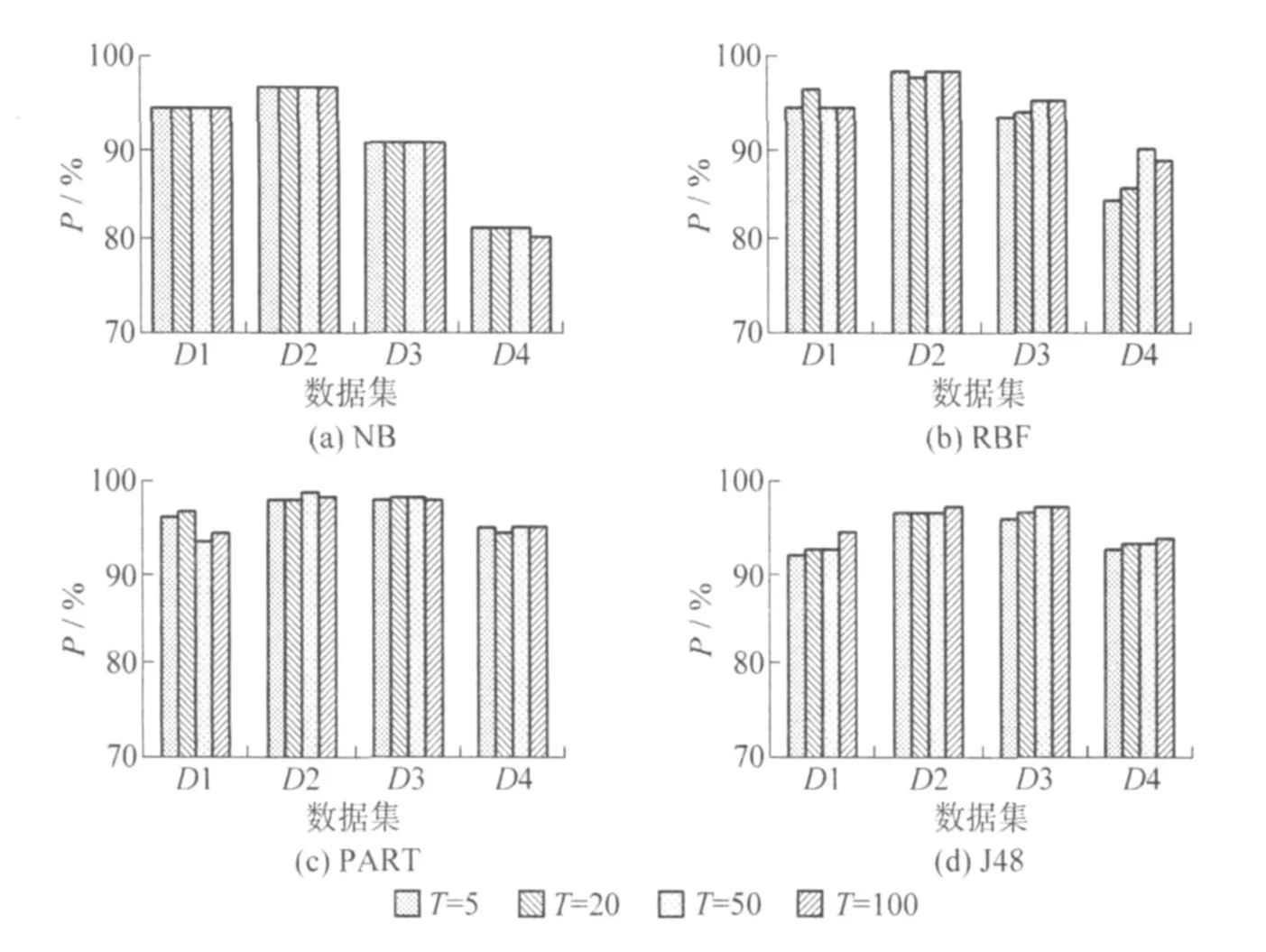
图 2 弱分类器个数对TPEL性能的影响Fig.2 The performance of TPEL when the countof the weak classifiers is changed

实验 3异构分类器集成实验.“异构”指在第 1阶段学习每个个体分类器的学习算法彼此不同.表3给出了本实验的结果.首先比较该实验中的 TPEL与 AdaBoostM1的性能.从该表可看出,D1、D3、D4这3个数据集在多数指标上都优于 AdaBoostM 1.仅在数据集 D2上,TPEL略差于 AdaBoostM 1.在 D2上,AdaBoostM1的 P值为 98.68%,L2在这一数据集上取得了 98%的总正确率,与 AdaBoostM 1接近;L1、L3的 P值也与 AdaBoostM1比较接近.可见,此时的 TPEL比 AdaBoostM 1要优秀许多.与 Bagging(见表 2)相比,本实验中的 TPEL在 4个数据集上的结果全面优于 Bagging.因此,不难得出结论,TPEL在集成异构分类器时,效果非常理想.

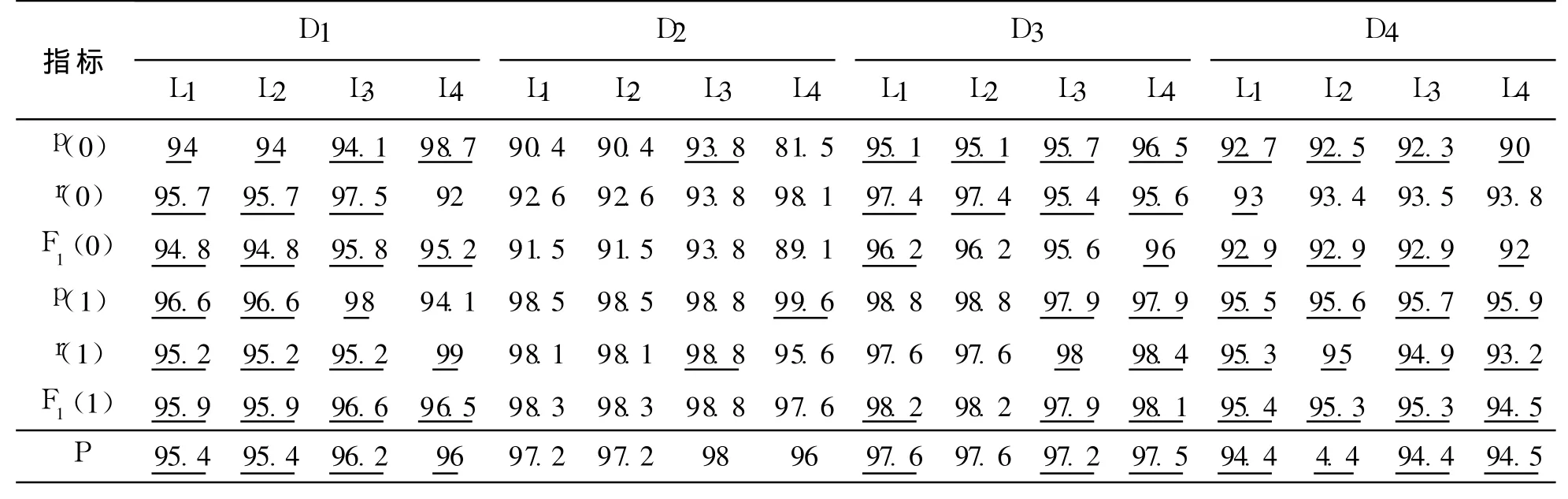
表 3 异构分类器集成的实验结果Table 3 The experimental results of combining multiple heterogeneous classifiers %

实验 4完全同构分类器集成.完全同构指第 1阶段和第 2阶段的学习算法相同.实验结果如表 4所示.从表 4可以看出,除 L2在 D1、D2两个数据集上比 NB稍差外,其他值大部分都优于 NB.仅从 P值分析,L1在 D1、D2上强于 Bagging,在 D3、D4上有所不及;L1仅在 D4上强于 AdaBoostM1.L2仅在 D1上强于 Bagging,其他数据集上与 Bagging接近;在 D3,尤其是在 D4上超过了 AdaBoostM1,在其他 2个数据集上接近.L3在 4个数据集上的都超过了 Bagging;在 D3、D4上超过了 AdaBoostM1,在 D1、D2上与AdaBoostM1的 P值有 1%左右的差距.L4在 D1、尤其是在 D4上,超过了 AdaBoostM1,在 D2、D3上也与AdaBoostM1的性能接近;在 D1、D2上超过了 Bagging.

表 4 完全同构分类器集成结果Tab le 4 The experimental resu lts of com bining the sam e classifiers %

当集成完全同构的分类器时,TPEL也取得了成功.尤其是当采用适当的弱学习分类器的学习算法时(如 L3),TPEL的性能超过 Bagging和 AdaBoostM 1的表现.

实验 5部分同构实验.结果见表 5部分同构指第 1阶段的学习算法相同,但第 2阶段采用与第 1阶段不同的学习算法.从表 5可以看出,在各种实验中,TPEL的大部分指标值比 NB的要好,尤其是 L3.结合实验 4可知,TPEL适用于部分同构或完全同构方式的集成.

表 5 部分同构实验的结果Table 5 The experim enta l resu lts of combining part o f the homogeneous classifiers %

实验 6稳定性实验.包括 4个子实验.

1)测试对稳定性算法 NB的集成情况.在 TPEL中,第 1阶段采用 10个 NB,第 2阶段采用 NB.

2)测试对稳定性算法 k-NN(k=5)的集成情况.在 TPEL中,第 1阶段采用 10个k-NN,第 2阶段采用NB.

3)测试对不稳定性算法 RBF的集成情况.在 TPEL中,第 1阶段采用10个 RBFNetwork,第 2阶段采用RBFNetwork.

4)测试对不稳定算法 J48的集成情况.在 TPEL中,第 1阶段采用 10个 J48,第 2阶段采用 J48.

4个子实验的实验结果如图 3所示.

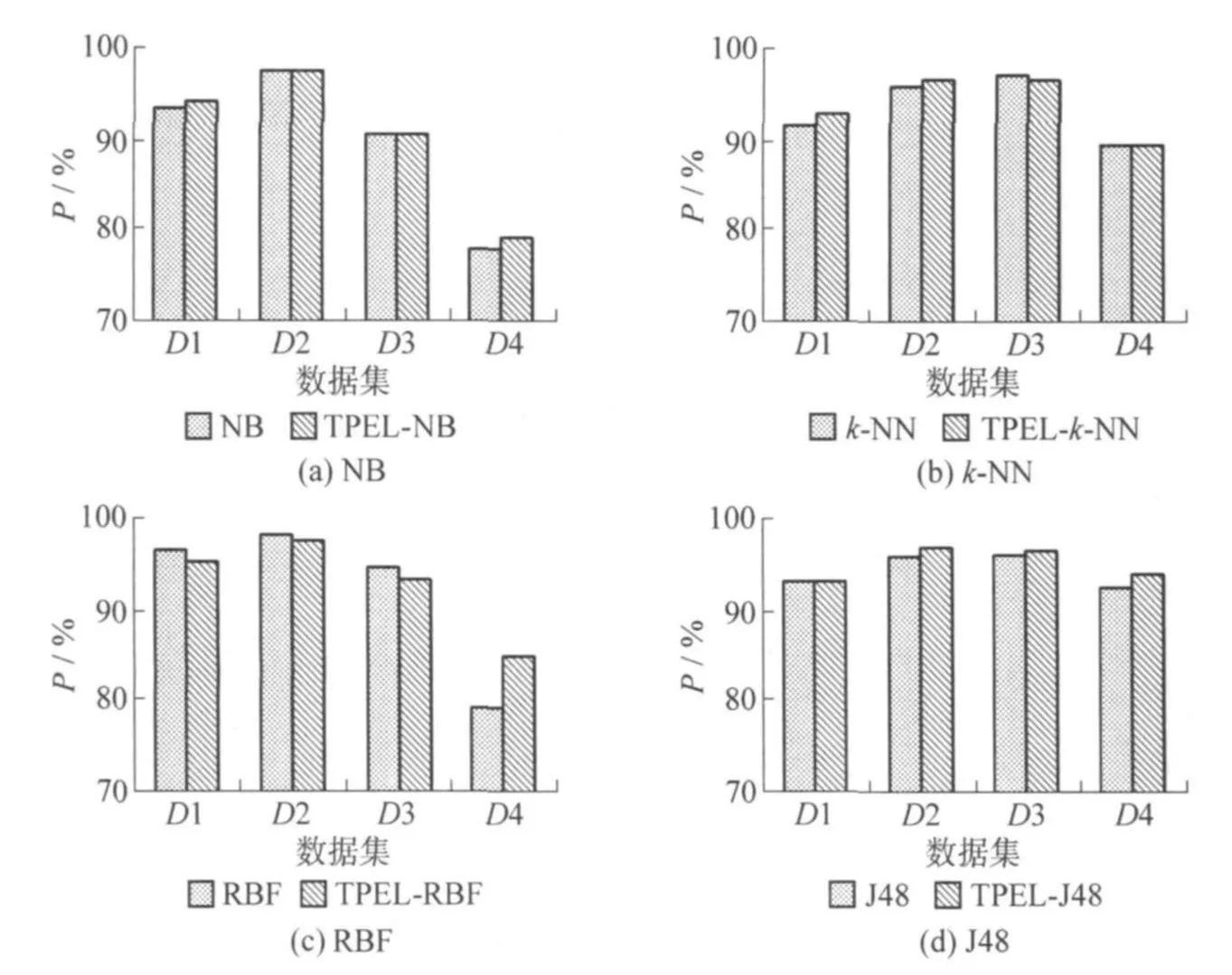
图 3 TPEL稳定性实验Fig.3 Stability experiment

图 3(a)、(b)表明,TPEL的结果与 NB的相当或有提高.这说明,TPEL适用于集成稳定算法,不像Bagging,对稳定学习算法的集成往往会使性能极大地降低.图 3(c)显示 TPEL在 D1、D3数据集上比 RBF Network的性能稍差,在 D2上相当,在 D4上比单个 RBFNetwork强许多.图 3(d)显示 TPEL在 4个数据集上都提高了 J48的性能.说明 TPEL适用于提升不稳定性算法的性能.

可见,对稳定或不稳定算法,用 TPEL集成都能从一定程度上改善分类精度.

实验 7 时间复杂度实验.表 6比较了 TPEL与其他算法的时间复杂度.TPEL的训练时间由 2部分组成,第 1部分来自于直接学习,第 2部分来自于间接学习.本实验中,TPEL第 1阶段集成了 NB、PART、J48、RBF Network;第 2阶段则采用 NB.由于第 1阶段的训练可以采用多线程并发执行方式,因此,第 1阶段的训练时间约等于所集成的 4种算法中的最长训练时间.从表 6可以看出,TPEL的时间比 AdaBoostM1的要短许多.TPEL间接学习的时间非常短(见加号后面的数字),几乎可以忽略不计.

上述实验从各个侧面分析了 TPEL的性能及特点.实验结果表明,TPEL是一种有吸引力的集成学习方法.TPEL的优势为:

1)不需要过多地考虑轮数 T的取值大小问题,因为 TPEL受 T的影响不大;

2)实现简单,训练时间短;

3)效果明显;

4)集成函数的形式并非一成不变,它随数据集及直接和间接学习过程中的学习算法的变化而变化.

表 6 时间复杂度比较结果Tab le 6 Compared resu lts of time com plexity s

3 结束语

在集成学习中,集成函数的形式通常是被事先设定的,如在 Bagging类或 Boosting类方法中,这往往导致不确定的性能.本文提出了 1种 2阶段集成学习的方法,其最大特点是利用学习算法学习集成的预测函数.实验结果表明,TPEL受集成的个体分类器个数的影响甚微;利用 TPEL集成异构的多个分类器时效果显著;利用 TPEL集成同构多个分类器时,绝大部分情况下取得了优于朴素贝叶斯等算法的结果;对稳定及不稳定学习器的集成效果都比较明显;TPEL具有较低的时间复杂度.

尽管本文只是在 2类文本分类的情况下验证了算法的性能,但 2类分类是多类分类的基础,不难将TPEL推广到多类的情况.

[1]苏金树,张博锋,徐昕.基于机器学习的文本分类技术研究进展[J].软件学报,2006,17(9):1848-1859.SU Jin-shu,ZHANG Bo-feng,XU Xin.Advances in machine learning based text categorization[J].Journal of Software,2006,17(9):1848-1859.(in Chinese)

[2]李文斌,刘椿年,陈嶷瑛.基于混合高斯模型的电子邮件多过滤器融合方法[J].电子学报,2006,34(2):247-251.LIWen-bin,LIU Chun-nian,CHEN Yi-ying.Combining multiple email filters of naive bayes based on GMM[J].Acta Electronica Sinica,2006,34(2):247-251.(in Chinese)

[3]刁力力,胡可云,陆玉昌,等.用 Boosting方法组合增强Stumps进行文本分类[J].软件学报,2002,13(8):1361-1367.DIAO Li-li,HU Ke-yun,LU Yu-chang,et al.Improved stumps combined by boosting for text categorization[J].Journal of Software,2002,13(8):1361-1367.(in Chinese)

[4]鲁湛,丁晓青.基于分类器判决可靠度估计的最优线性集成方法[J].计算机学报,2002,25(8):890-895.LU Zhan,DING Xiao-qing.An optimal linear combination method by evaluating the reliability of individual classifiers[J].Chinese Journal of Computers,2002,25(8):890-895.(in Chinese)

[5]李凯,黄厚宽.小规模数据集的神经网络集成算法研究[J].计算机研究与发展,2006,43(7):1161-1166.LIKai,HUANG Hou-kuan.Study of a neural network ensemble algorithm for small data sets[J].Journal of Computer Research and Development,2006,43(7):1161-1166.(in Chinese)

[6]姜远,周志华.基于词频分类器集成的文本分类方法[J].计算机研究与发展,2006,43(10):1681-1687.JIANG Yuan,ZHOU Zhi-hua.A text classification method based on term frequency classifier ensemble[J].Journal of Computer Research and Development,2006,43(10):1681-1687.(in Chinese)

[7]周志华,陈世福.神经网络集成[J].计算机学报,2002,25(1):1-8.ZHOU Zhi-hua,CHEN Shi-fu.Neural network ensemble[J].Chinese Journal of Computers,2002,25(1):1-8.(in Chinese)

[8]唐伟,周志华.基于Bagging的选择性聚类集成[J].软件学报,2005,16(4):496-502.TANG Wei,ZHOU Zhi-hua.Bagging-based selective clusterensemble[J].Journal of Software,2005,16(4):496-502.(in Chinese)

[9]DIETTERICH T G.Machine learning research:four current directions[J].AIMagazine,1997,18(4):97-136.

[10]ZHOU Zhi-hua,TANGWei.Selective ensemb le of decision trees[C]∥Lecture Notes in Artificial Intelligence.Berlin:Springer,2003,26391:476-483.

[11]ZHONG N,MATSUNAGA T,LI U C N.A text mining agents based architecture for personal e-mail filtering and management[C]∥Lecture Notes in Computer Science.Berlin:Springer,2002:329-336.

[12]樊兴华,孙茂松.一种高性能的两类中文文本分类方法[J].计算机学报,2006,29(1):124-131.FAN Xing-hua,SUN Mao-song.A high performance two-class Chinese text categorization method[J].Chinese Journal of Computers,2006,29(1):124-131.(in Chinese)

[13]BREIMAN L.Bagging predictors[J].Machine Learning,1996,24(2):123-140.

[14]SCHAPIRER E.The strength of weak learn ability[J].Machine Learning,1990,5:197-227.

[15]FREUND Y.Boosting a weak algorithm bymajority[J].Information and Computation,1995,121(2):256-285.

[16]OPITZ D,MACLIN R.Popular ensemble methods:an empirical study[J].Journal of Artificial Intelligence Research,1999,11:169-198.

[17]The University of Waikato.Weka开发包[DB/OL].(1998-01-02)[2009-11-02].http:∥www.cs.waikato.ac.nz/ml/weka/

[18]ANDROUTSOPOULOS I.PU 1数据集 [DB/OL].(2000-03-28)[2010-03-09].http:∥www.aueb.gr/users/ion/publications.html

[19]SAKKISG.Lingspam数据集[DB/OL].(2003-05-16)[2010-03-09].http:∥www.aueb.gr/users/ion/publications.html

[20]Apache Software Foundation.Spam Assassin数据集[DS/OL].(2002-02-08)[2010-03-09].http:∥spamassassin.apache.org/pub liccorpus/

[21]HEWLETT-PACKARD L.Spambase数据集[DB/OL].(1998-06-10)[2010-03-09].http:∥www.ics.uci.edu/～m learn/databases/spambase/

[22]YANG Y,PEDERSEN J O.A comparative study on feature selection in text categorization[C]∥Proc of the 14th International Conference on Machine Learning.[S.l.]:Morgan Kaufmann,1997:412-420.