发电机和负荷模型对暂态稳定性分析的影响

李 锐,高 雁

(山西电力职业技术学院,山西太原 030021)

发电机和负荷模型对暂态稳定性分析的影响

李 锐,高 雁

(山西电力职业技术学院,山西太原 030021)

针对发电机和负荷的数学模型,然后以一个3台发电机7个节点系统图为例,应用电力系统分析综合程序进行仿真,分析不同的发电机模型和负荷模型对电力系统暂态稳定性分析的影响,得出采用不同的元件模型,对电力系统暂态稳定性计算的影响是不同的。

发电机模型;负荷模型;暂态稳定性;电力系统

0 引言

在电力系统的暂态稳定性的仿真研究中,发电机和负荷模型的影响对其仿真结果的影响尤为突出。发电机模型根据计算精度的要求,对电势处理的不同,则会有从2阶到6阶各种不同的模型。负荷模型是指描述负荷端口的功率或电流随其端口电压和频率变化的数学方程和相应的参数。选用何种合理的负荷模型对电力系统暂态稳定仿真分析的结果有重要影响。目前,感应电动机和恒阻抗并联的综合负荷模型被我国大部分电网所采用。本文选用电力系统综合程序仿真软件PSASP(Power System Analysis Software Package)6.2版(Window s版)作为基础程序,比较不同发电机和负荷模型类型及其参数对电力系统暂态稳定性的影响。

1 发电机的数学模型

程序中共有6种不同精度的同步电机模型供选用,其中0型,E′电势恒定的经典模型 (2阶);1型,E′q电势恒定的模型 (2阶);2型,E′q电势变化的模型 (3阶);3型,E″q、E″q、电势变化的模型 (5阶);4型,E″电势恒定的模型 (2阶);5型,E″q、E″d电势变化的模型 (4阶);6型,E″q、

式中:T′d0 ——d轴开路暂态时间常数;

t ——E′q对时间的变化率;

E fd ——励磁电压;

xd、x′d——发电机d轴的同步电抗、暂态电抗;

Id ——电流的d轴分量;

E′q——q轴瞬变电动势, 即 X′d后面的电动势。E″d、E″q、E″d电势变化的模型 (6阶)。当精度要求不高时,可采用2阶模型;当要计及励磁系统时,可采用3阶和5阶模型;当要计及q轴转子阻尼绕组Q和g,可采用4阶或6阶模型。

在计及发电机转子d轴励磁绕组f及阻尼绕组D的次暂态和暂态电磁过程、q轴阻尼绕组Q和g的次暂态及暂态电磁过程时,发电机转子绕组的电磁暂态过程可用定子绕组电动势变化来描述,其方程式见式 (1)、式 (2)、式 (3)、式 (4)[1-2]。

式中:T″d0——d轴开路的次暂态时间常数;

E″q ——q轴超瞬变电动势,即 X″d后面的电动势;

x″d ——d轴次暂态电抗。

式中:T′q0 ——q轴开路暂态时间常数;

E′d——d轴瞬变电动势,即X″q后面的电动势;

在电力系统的仿真计算中,发电机数学模型就是基于上述5个方程的。

2 负荷的数学模型

负荷的数学模型有负荷静态模型、负荷动态模型。

2.1 负荷静态模型

负荷静态模型反映了负荷有功、无功功率随频率和电压缓慢变化的规律,可用代数方程或曲线表示。其中负荷随电压变化的特性称为负荷电压特性,而随频率变化的特性称为负荷频率特性。静态负荷模型主要代表商业和民用用户,主要有多项式模型和幂函数模型两种。计及负荷电压特性和频率特性时,两种模型分别见式 (6)、式 (7)。

2.2 负荷动态模型

在系统电压和频率快速变化时,应考虑负荷的动态特性,并用微分方程描写,称之为负荷动态模型。由于电力系统的动态负荷主要成分是感应电动机,因此,通常用感应电动机模型作为负荷动态模型。根据不同的应用领域和分析计算目的,人们提出了多种感应电动机的模型。在PSASP中,采用的为忽略定子绕组暂态,考虑感应电动机转子回路电磁暂态过程和转子机械运动暂态过程的负荷动态模型,其数学模型转子运动方程、电势变化方程、电压方程式分别见式 (8)、式 (9)、式 (10)。

3 负荷模型对暂态稳定的影响算例分析

负荷模型对暂态稳定的影响是通过负荷功率随电压、频率的变化影响作用在各发电机上的电磁功率,进而影响对各发电机组起加速或减速的剩余转矩。选择3台发电机7个节点系统作为研究对象,考察不同负荷模型及其参数对暂态稳定极限切除时间的影响。潮流计算采用牛顿-拉夫逊法,稳定计算则采用 “综合程序”内定的经典隐式梯形法,积分步长为0.01 s,积分时段为5 s。采用的故障是在线路3上0.02 s发生A相接地短路,0.11 s切除故障。以下取的是发电机G2和平衡机S1的功角值,判断暂态稳定的依据就是在第一、二摆不失步。系统图如图1所示。

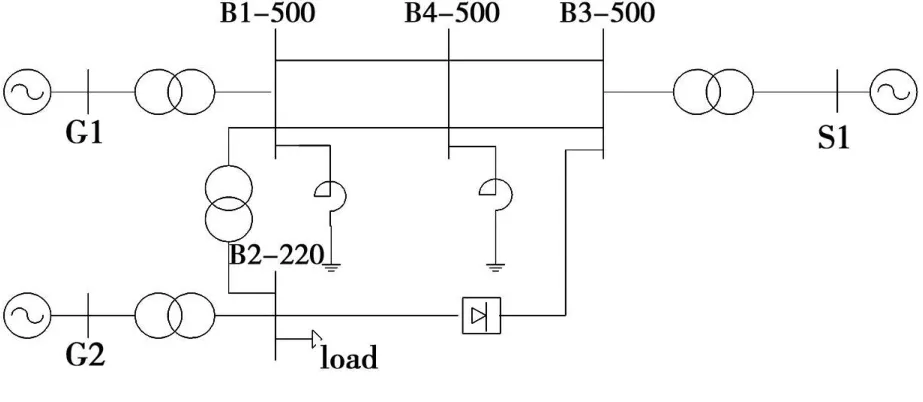
图1 3台发电机7个节点系统图

3.1 发电机模型的影响

发电机G1分别采用经典模型和详细模型,来比较一下发电机的功角变化情况。

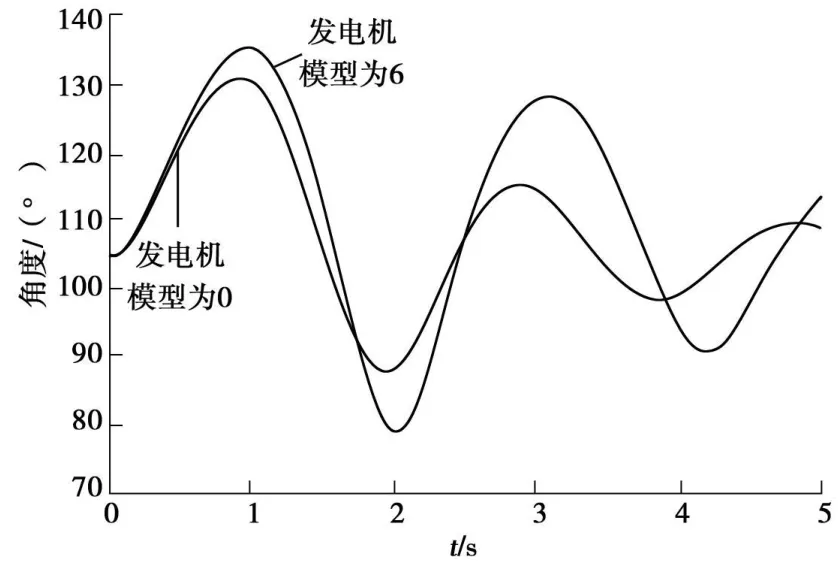
图2 发电机G 2-S1的功角曲线图

从功角曲线图中可以看出,模型6(即详细模型)曲线要比模型0(即经典模型)的曲线振荡的缓慢,衰减的时间长。

从仿真结果中可以看出,采用不同精度的同步发电机数学模型可以看到,暂态稳定趋于稳定的时间是不同的。采用高阶的同步发电机数学模型更能详细地仿真出功角的变化情况。

3.2 不同负荷模型的影响

在同一个故障下,不同的负荷模型结构对系统的稳定影响不一样,同样在同一个故障下,同一个负荷模型结构,不同的参数对系统的稳定性影响也不同。有的参数对系统的影响大,有的参数对系统的影响小。

负荷模型分别采用100%恒阻抗、恒电流、恒功率、感应电动机负荷模型时,来比较一下这几种负荷模型对暂态稳定性的影响程度。

恒阻抗和恒电流负荷模型与恒功率和感应电动机模型相比,在短路故障下有较强的功角稳定性。可以从表1功角值看出来。

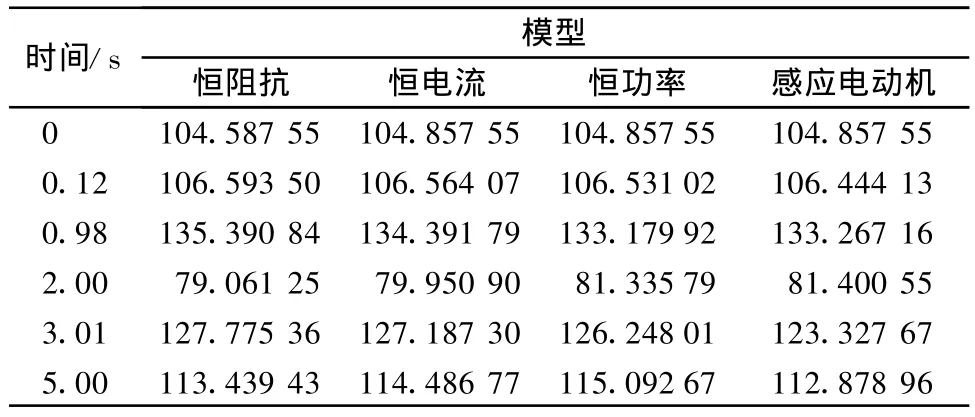
表1 不同负荷模型下的功角值(°)

3.3 关于感应电动机负荷对暂态稳定性的影响

对于感应电动机中的参数很多,在这里主要研究参数 X m、R s、X s、R r、X r、T J对系统的稳定性影响[3]。

3.3.1 定子电抗X1和转子电抗X2

表2为取不同的定子电抗值时的功角值。

表2 感应电动机负荷定子电抗对功角值的影响

从表2可以看出,感应电动机定子电抗对发电机的功角值影响很微小,同理,由仿真结果可以看出,转子电抗对暂态稳定性的影响也很小。

3.3.2 转子电阻R2

表3给出了不同的转子电阻对功角值的影响程度。

表3 感应电动机转子电阻对功角值的影响

从表3的结果可以看出,转子电阻对暂态稳定性的影响也是比较小的。

3.3.3 感应电动机负荷惯性时间常数的影响

表4中列出了不同感应电动机惯性时间常数TJ所对应的功角值。

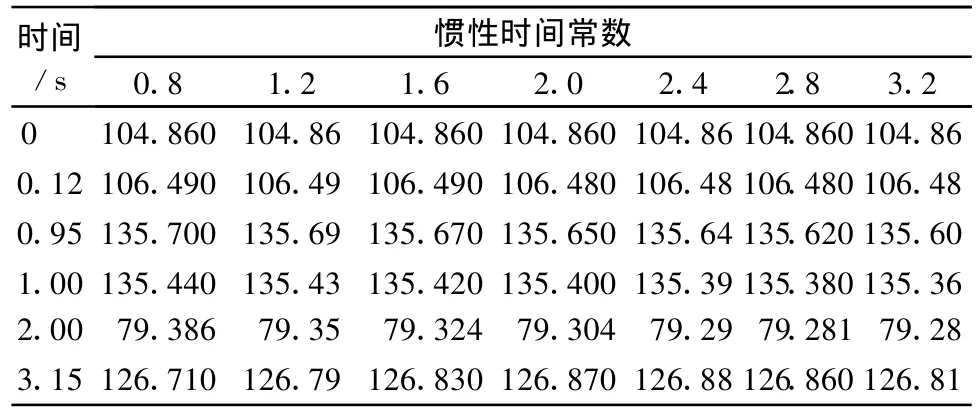
表4 感应电动机负荷惯性时间常数对功角值的影响

从表4可以看出,惯性时间常数对暂态稳定性的影响是相对较小的。

由感应电动机负荷惯性时间常数对功角值的影响的仿真计算中可以看出,在电力系统的暂态稳定性仿真中,负荷模型的不同对系统的稳定性的影响也不同。因此,在暂态稳定的仿真计算中,应合理的选择负荷模型。

4 结论

影响暂态稳定性的两个较为突出的方面,即发电机、负荷模型对暂态稳定性的影响。由仿真结果可以看出,选择合适的发电机和负荷模型,对分析电力系统的暂态稳定计算有着很重要的意义。

[1] 吴红斌,丁明,李生虎,等.发电机和负荷模型对暂态稳定性影响的概率分析 [J].电网技术,2004,28(1):19-21.

[2] 倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002:48-102.

[3] 孙华东,周孝信,李若梅.感应电动机负荷参数对电力系统暂态电压稳定性的影响[J].电网技术,2005,29(23):1-6.

The Influences of Generator Model and Load Model on Transient Stability Analysis

LIRui,GAO Yan
(ShanxiElectric Power Technical College,Taiyuan,Shanxi 030021,China)

This paper describes themodel o fgenerator and load.Taking th ree pow er generators as examp le,the influences of different generator models and load models on the power system transient stability are emphatically analysed by using Pow er System Analysis Sof tware Package(PSASP),the resu lt of which show s that the em p loyment of different models exerts different influences on the transient stability of pow er system.

generatormodel;load model;transient stability;pow er system

TM 712

A

1671-0320(2010)03-0054-04

2010-03-02,

2010-05-04

李 锐 (1957-),女,山西太原人,2006年毕业于中央电大教育管理专业,讲师,主要研究方向为电能计量和二次回路;

高 雁 (1978-)女,山西长治人,2008年毕业于太原理工大学电力系统及其自动化专业,硕士,从事电力系统分析工作。