三轴应力状态下砂砾料浸水变形特性试验研究
付 江,方绪顺,秦桂林,付皓鸫
(1.长江下游水文水资源勘测局九江水文站,江西 九江332000;2.南京水利科学研究院,江苏 南京210024)
0 前 言
土石坝的浸水变形是引起坝体裂缝的一个重要原因,将危及土坝特别是高土石坝的安全。除加强原型监测外,室内试验和对土石坝初次蓄水及水位骤降的应力应变分析,是土石坝筑坝技术研究的重要手段。
早在1973年,Nobari和Duncan[1]首先用三轴试验通过“单线法”和“双线法”分别研究了浸水变形,同时得出结论,浸水变形可以由干湿两种应力—应变曲线来求。国内在1985年~1989年期间,先后有南京水利科学研究院、成都科技大学、清华大学和黄河水利科学研究院等兄弟院校进行过室内浸水变形试验研究,并建立了相应的浸水变形模型[2,3]。
鉴于当时的试验条件,试验总结出的成果没有很好地运用到有限元计算中去,而湿化变形在心墙坝的有限元计算中占有重要的地位,它的存在,使土坝的局部可能产生完全的塑性状态,甚至出现受拉状态。因此,利用现代科技手段进一步研究浸水变形特性是一个重要的新课题。
笔者在前人所做工作的基础上,利用引进的VJ非饱和土三轴仪,进一步开展单线法试验研究,修正湿化变形计算模型,得出了浸水变形计算经验公式。
1 试验用料的选取
试验用料是新疆引额济乌“635”水利枢纽大坝的坝壳砂砾石料。由于试样直径的限制,在试验过程中,将砂砾石料中大于5 mm的颗粒筛去,取小于5 mm颗粒的砂土,其颗粒级配曲线见图1。试验土料的土粒比重 G=2.72,最大干密度 ρdmax=1.99 g/cm3,最小干密度 ρdmin=1.50 g/cm3,试样干密度 ρd=1.80 g/cm3,相对密实度 Dr=0.68,不均匀系数 Cu=13.71。
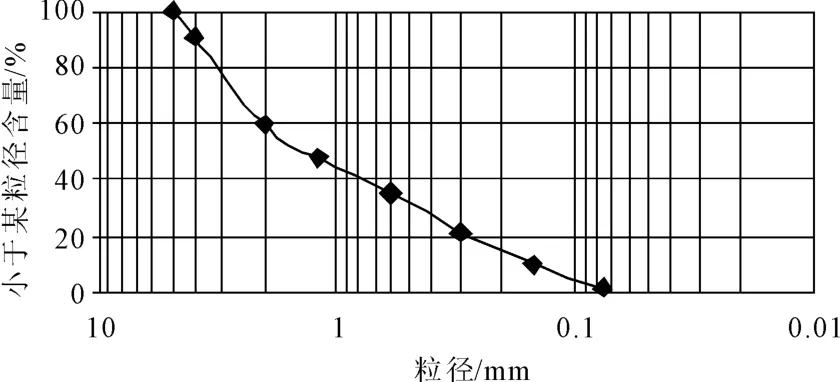
图1 试验用砂砾料级配曲线
2 仪器设备
试验仪器设备选用英国进口的VJ非饱和土三轴仪,其结构示意图如图2所示,试验过程中的应力和变形等数据自动采集。跟常规三轴仪相比具有以下特点:
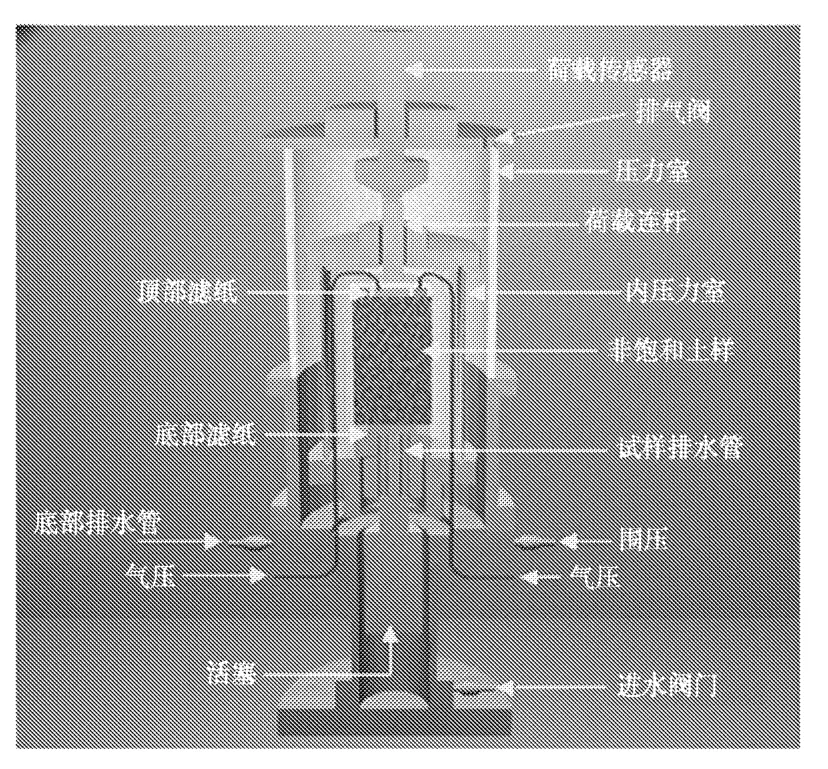
图2 VJ非饱和土三轴仪结构示意图
(1)采用双压力室,利用内压力室进、出水的体积测量非饱和土的体积变形。
(2)采用精确的体变仪自动跟踪测量试样的体变代替以前的人工测读的方法,体变仪的进出水量即为体变。
(3)试样偏应力采用连续加荷代替以前分级加荷的方式,荷载的大小通过轴力传感器测量。
(4)围压通过加水压的方式加载,通过压力传感器测量围压的大小。
(5)轴向变形是通过数字式千分表测量。
(6)在整个试验过程中所用的水都为无气水。
(7)最大轴力:10 kN 精度±1 N
最大围压:1 700 kPa 精度±0.1 kPa
最大体变:100 mL 精度±0.1 mL
试样尺寸:直径50 mm高100 mm
3 试验方案
在分析总结前人所做研究的基础上,本试验分3组合计15个试样。所有试样干密度控制为1.80 g/cm3,选择3种不同的围压,即 σ3=200 kPa、400 kPa、600 kPa,最大围压与依托工程的实际最大侧压力相近。在3种不同的围压下,分别进行干砂等压固结浸水变形试验、干砂固结排水剪切试验和3种不同的应力水平SL=0.25、0.5、0.75下浸水变形试验。试验加荷速率为100 kPa/h。
4 试验方法
4.1 制试样
根据体积称取砂重后,分3次装入承膜筒内,每次控制高度在3.5 cm左右,装入后轻轻敲击承膜筒再击实至设定密度。试样高度h=10.8 cm,直径φ=5.0 cm。为确保试样尺寸精度,拆除承膜筒后再行量测试样的高度和直径。
4.2 干砂剪切试验
装好试样后加围压,待固结稳定后,加轴向荷载,仪器自动记录每级荷载下的轴向变形和体积变形,直到剪切破坏。
4.3 干砂在等压固结作用下浸水变形试验
装好试样后,加固结压力,待固结稳定后。在恒定的应力下从试样底部进水,使其逐渐饱和。当同一时间间隔内出水量等于入水量即认为试样已饱和。浸水变形的稳定标准采用15 min内垂直变形不超过1%mm。浸水饱和时间大约在1 h左右。
4.4 干砂在剪切状态下浸水变形试验
装好试样后,加固结压力,待固结稳定后,加轴向压力(σ1-σ3)剪切,轴向压力分别加到峰值荷载的25%、50%、75%,即 SL=(σ1-σ3)/(σ1-σ3)f=0.25、0.5、0.75。待变形稳定后,在恒定的应力下从试样底部进水,使其逐渐饱和。当同一时间间隔内出水量等于入水量即认为饱和。浸水变形的稳定标准采用15 min内垂直变形不超过1%mm。浸水饱和时间大约在1 h左右。然后再加轴向压力剪切,荷载匀速自动加载,直至破坏。
5 试验成果的整理
5.1 浸水变形的应力应变及体应变
5.1.1 各向等压条件下浸水变形试验
干砂各向等压浸水变形试验结果绘成εv~t之间的关系如图3所示(图中,t=0为等压固结开始时刻),从图中可以看出,干样在固结过程中εv随围压的增加其值逐渐变大。待干样固结稳定后,试样开始从底部浸水,在浸水过程中,曲线 εv~t呈较明显陡增的直线段。待试样完全饱和后,εv~t呈明显的直线段,说明浸水变形趋于稳定。
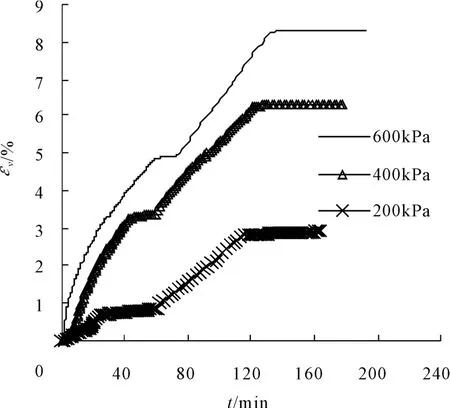
图3 各向等压浸水变形εv~t过程线
浸水变形引起的体应变增量统计表见表1所示。

表1 各向等压浸水变形产生的体应变增量统计表
从上表可以看出,各向等压浸水变形产生的体积应变增量随围压的增加而增大。其Δεv~σ3关系曲线如图 4所示。从图中可以看出Δεv~σ3之间接近对数关系。
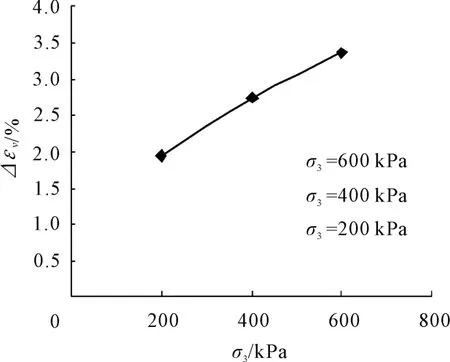
图4 Δεv~ σ3之间关系曲线
5.1.2 三轴剪切条件下的浸水变形试验
依据三轴剪切试验的结果,整理出各个侧压力下(σ1-σ3)~εa、εv~εa之间的关系。为便于比较将在同一种围压作用下的干砂及饱和砂试验、浸水变形试验绘于同一张图上如图5、图6、图7所示,从图中可看出:
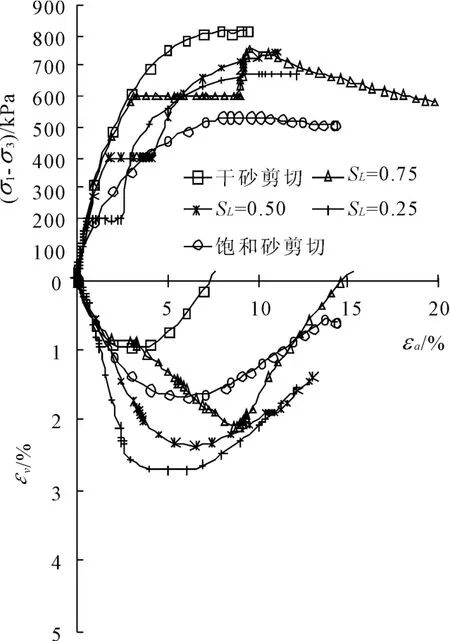
图5 砂砾石料在σ3=200 kPa下浸水试验结果
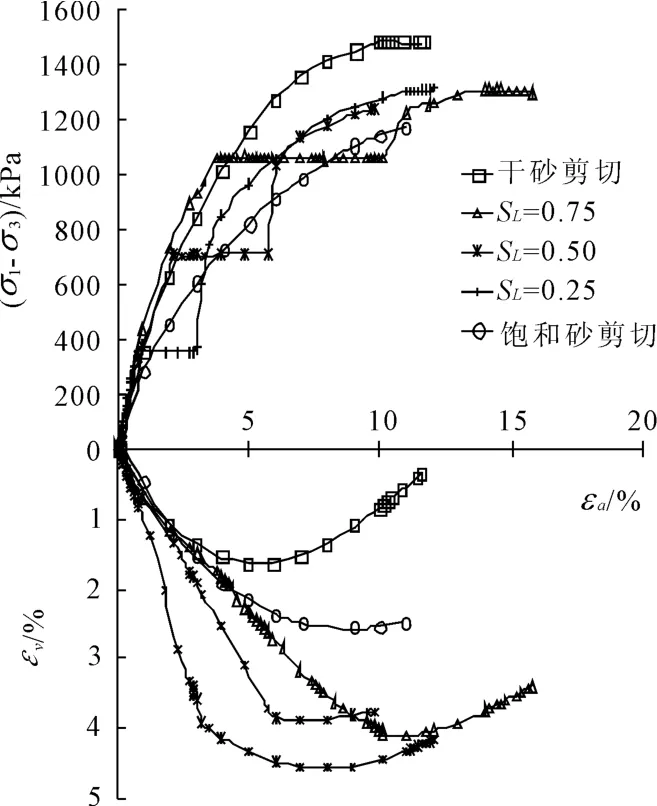
图6 砂砾石料在σ3=400 kPa下浸水试验结果
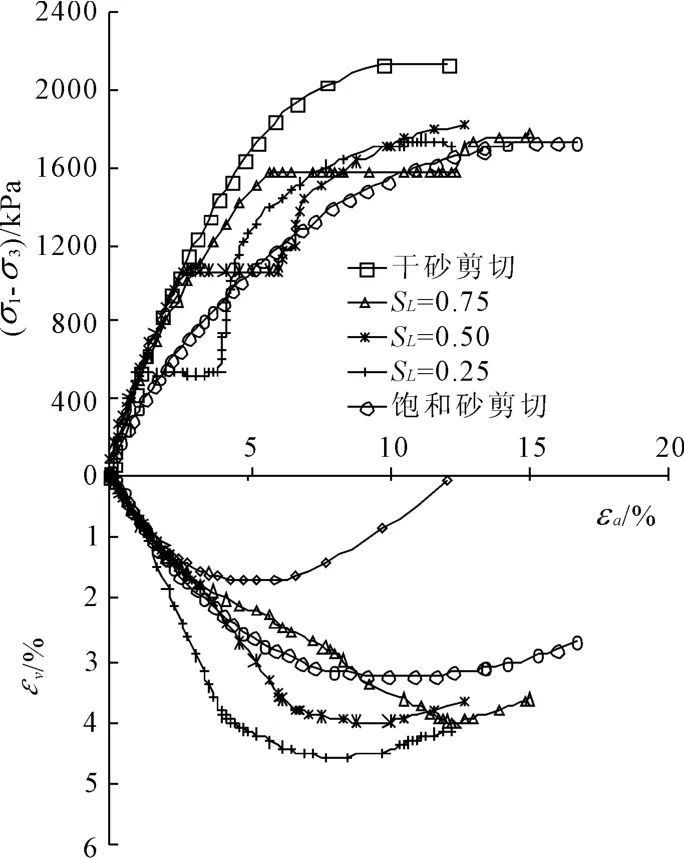
图7 砂砾石料在σ3=600 kPa下浸水试验结果
(1)在同一种σ3条件下,干砂浸水前同一围压下的应力应变曲线基本重合。浸水过程中的应力、应变曲线(σ1-σ3)~ εa表现为水平直线段,即维持轴向附加应力(σ1-σ3)不变,εv~ εa呈较明显陡增的直线段。浸水后继续对试样增加(σ1-σ3),直至剪切破坏。浸水后试样的强度(σ1-σ3)f比干样低,比饱和样高。
(2)在同一应力水平下,浸水后试样的强度(σ1-σ3)f随围压的增加其值增大。
(3)干砂在某一状态下浸水变形引起的轴向应变与体应变增量比相同应力状态下干砂与饱和砂之间的轴向应变之差及体应变之差都要大。亦即“单线法”比“双线法”测出浸水变形引起的轴向应变增量及体应变增量要大,尤其在低应力水平下,“单线法”要比“双线法”大100%。进一步说明在考虑浸水变形时,用“双线法”代替“单线法”不尽合理,如有条件要进行“单线法”试验。
浸水变形引起的轴向应变增量、体应变增量、径向应变增量和偏应变增量统计表见表2所示。
从表和图中可以看出:
(1)同一围压下浸水变形产生的轴向应变和偏应变增量随应力水平的增大而增大,而体应变增量则相反,随应力水平的增大而减小。
(2)同一应力水平下浸水变形产生的轴向应变增量、体应变和偏应变增量均随围压的增加而增大,但浸水变形引起的体应变增量随围压的增大有趋于稳定的趋势。
(3)当应力水平SL=0.25时,浸水变形引起的体应变增量大于轴向应变增量,说明低应力水平下浸水变形主要表现为压缩。
(4)当应力水平SL进一步增大时,浸水变形引起的轴向应变增量和偏应变增量会很快增加并远远超过相同围压下的体应变增量,而此时水平向应变增量小于零,说明较高应力水平下浸水变形主要表现为沉降及水平膨胀。

表2 不同应力水平下浸水变形产生的应变增量统计表
6 浸水变形引起应变增量计算公式
为了在坝体应力应变分析过程中考虑浸水变形而引起的应变增量,需要通过以上试验成果整理出体应变增量Δεv~σ应力之间的函数关系以及偏应变增量Δγ~σ应力之间的经验表达式。假定体积应变增量在试样各向同性和等压固结条件下可分解成两部分,一部分是由于围压 σ3引起的,另一部分是由于偏应力引起的;偏应变仅由偏应力引起的。
根据本文的砂砾石料试验结果,依据Δεa~ SL、Δεv~ SL和Δγ~ SL关系以及 Δεa~ σ3、Δεv~ σ3和Δγ~ σ3关系整理出以下浸水变形增量计算表达式:
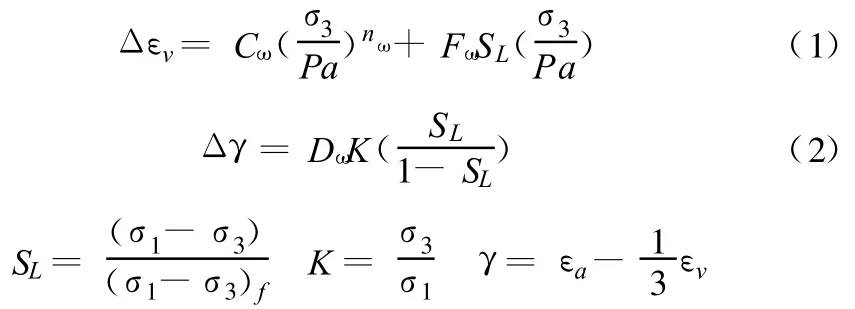
式中:Δεv为体应变增量;Δγ为偏应变增量;σ3为围压;SL为应力水平;Pa为大气压力;K为侧压力系数;γ为偏应变;εv为体应变;εa为轴向应变;Cω、nω、Fω、Dω为试验参数。
7 计算公式参数整理
7.1 体应变增量计算参数整理
利用干砂各向等压作用下浸水变形引起的体应变增量在双对数纸上点绘 Δεv~ σ3/Pa相关线,可整理得到参数Cω、nω,其中 Cω为该相关线的截距,nω为该相关线的斜率。
依据三轴剪切试验结果,通过点绘不同围压下偏应力引起的体应变增量与应力水平和围压之间的关系曲线,即相关线,整理参数Fω,其中Fω为不同围压下该相关线斜率的算术平均值,Δε′V等于三轴剪切浸水变形引起的体应变增量与相同固结压力下各向等压浸水变形引起的体应变之间的差值,即上述表2中的体应变增量与表1中相应围压下体应变增量之差。
7.2 偏应变增量计算参数整理
假定浸水变形引起的偏应变增量与应力水平和侧压力系数有关,通过点绘不同围压下相关线整理参数Dω,其中Dω为不同围压下该相关线斜率的算术平均值。
7.3 整理出的计算参数
整理得出的经验表达式计算参数见表3。

表3 参数统计表
8 结 语
通过对砂砾料的固结和剪切状态下浸水变形的试验研究,得到以下几点结论:
(1)砂砾石料各向等压浸水变形引起的体应变增量Δεv随围压σ3的增加而增大。其与围压之间的关系在双对数坐标上可以表示为一条直线。
(2)在同一围压作用下,砂砾石料在不同偏应力状态下浸水,引起的体应变增量随应力水平的增加而减小,且其增量均小于同一围压无偏应力状态下的浸水变形引起的体应变增量。
(3)砂砾石料的浸水变形引起的体应变增量包括两部分,一部分是围压σ3引起的增量,另外一部分是偏应力 q引起的增量,前者随围压σ3的增加而增加,而后者与应力水平SL有关,随着应力水平SL的增加而减小。
(4)浸水变形引起的偏应变增量Δγ与应力水平SL和侧压力系数K有关,且随着应力水平SL的增加而增加,与变量之间的关系近似成一直线关系。
[1] Nobari E S,Duncan J M.Movements in Dams due to Reservoir Filling[C]//Proceedings of Specialty Conference onPerformance of Earth and Earth Supported Structures.[s.l.]:[s.n.],1972:797-815.
[2] 朱百里,沈珠江.计算土力学[M].上海:上海科学技术出版社,1990:289-308.
[3] 李广信.堆石料的湿化试验和数学模型[J].岩土工程学报,1990,12(5):198-205.

