用多尺度慢度－时间相关法提取反射纵波的方法研究

范宜仁，张文静，邓少贵，孟凡增

（1.中国石油大学，山东东营257061；2.中国石油渤海钻探工程有限公司测井公司，天津300200）

0 引 言

在信号处理中，与传统傅里叶（Fourier）变换和窗口傅里叶变换相比，小波变换具有在时间域和频率域对信号进行局部化的特点，在声波信号处理中有着广泛的应用前景。阵列声波测井可对井壁及井壁附近传播的整个波列进行记录，位于滑行纵波和滑行横波之间的反射纵波在井旁裂缝识别中有很好的应用效果［1－3］，但反射纵波的能量一般都比较弱，难于提取。本文利用多尺度相关方法处理声波全波列，提取反射纵波［4］，在实际应用中取得了很好的效果。

小波的多尺度特性能够将声波全波列中不同模式波分解在不同的尺度上，选取合适的小波及尺度，压制其他高能量模式波，增强小信号，实现反射纵波的初步提取［5－7］。反射纵波与滑行纵横波的频率比较接近，仅仅通过多尺度分析不能将二者分离，利用小波变换保留时域特征这一特点，将常用的慢度时间相关法［8］与多尺度方法结合，求得不同尺度下的慢度－时间相关图，保留相关性好的反射纵波区域，切除其它区域，得到能量小的反射纵波。

1 多尺度慢度－时间相关法基本理论

1.1 多尺度理论

本文所研究的多尺度分析方法基于小波的基础之上，根据声波全波的特征和所要达到的目标，选用Kingsbury等人提出的双树复小波［9－11］。

双树复小波（DT-CWT）采用二叉树结构的2路DWT，一树生成变换的实部；一树生成虚部（见图1）。对于第1层分解，如果2树滤波器之间的延迟恰是1个采样间隔，就可以确保b树中第1层的二抽取正好采样到a树中因二抽取所丢掉的采样值；对于以后的各层分解，为了保证2树在该层和所有前层上产生的延迟差的总和相对于原始输入为1个采样周期，2树对应滤波器的相频响应之间应有1／2个采样周期的群延迟，且2个滤波器的幅频响应相等。为了保证线性相位而采用双正交小波变换，要求一树的滤波器为奇数长；另一树的滤波器为偶数长。如果在每树的不同层次间交替采用奇偶滤波器，那么这2树就会呈现好的对称性。Q-Shift双树复小波变换以更巧妙的方法实现2树对应滤波器之间的1／2采样周期延迟。双树复小波变换具有近似平移不变性、良好方向选择性、完美重构性、有限数据冗余性等优点。

为了寻找空间L2（R）的基，先从L2（R）的某个子空间出发，在这个子空间中先建立基底，然后利用简单变化，把这个基底扩充到空间L2（R）上，以形成一组基，这就是多尺度分析方法。

以一维情况为例，信号的多尺度分析算法可表示为

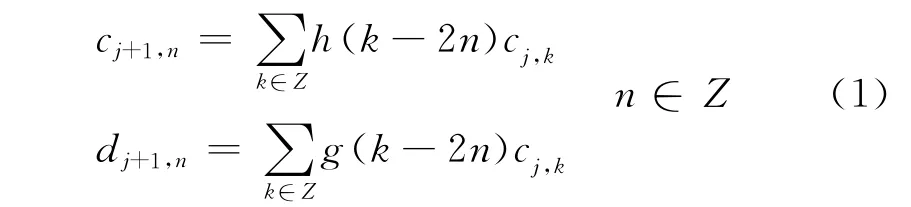
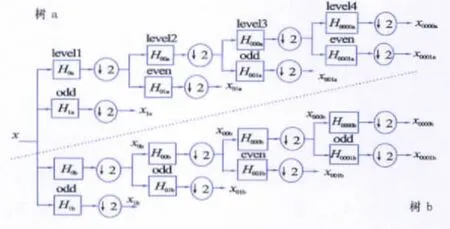
图1 双树复小波变换

因cj＋1，n是cj，k的低频逼近，dj＋1，n是cj，k的高频细节，所以h和g可看作低通和高通滤波器系数。引入滤波器H和G，其中H＝h（k－2n），G＝g（k－2n），则式（1）简化为

当j取一系列整数时，便实现了对信号的多尺度分解。j是多尺度分解的层数。相应的多尺度重构算法为

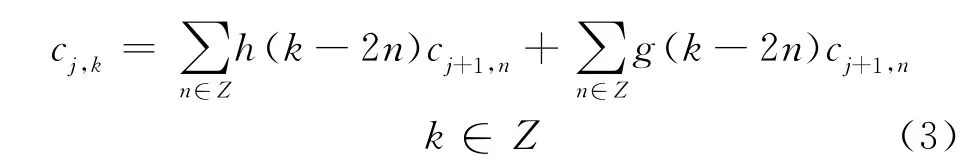
其简写形式为

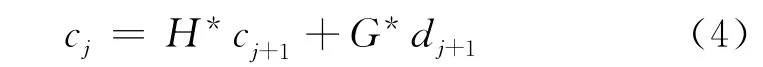
式中，H＊和G＊分别是H和G的对偶算子。分解和重构算法示意图分别见图2（a）和图2（b）。

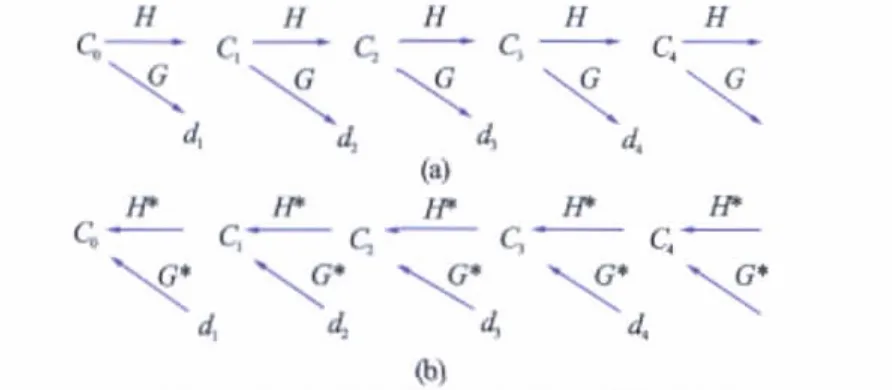
图2 信号的多尺度分解和重构算法

1.2 慢度－时间相关法（STC）

慢度－时间相关法适用于频散的偶极子阵列信号分析以提取横波慢度。由声波测井原理可知，井中激发的模式波在远场可以看作沿井轴匀速传播。因而在接收器阵列上各模式波应该具有一定的相关性。通过设置对比窗口，得到依赖于慢度和时间的相关函数

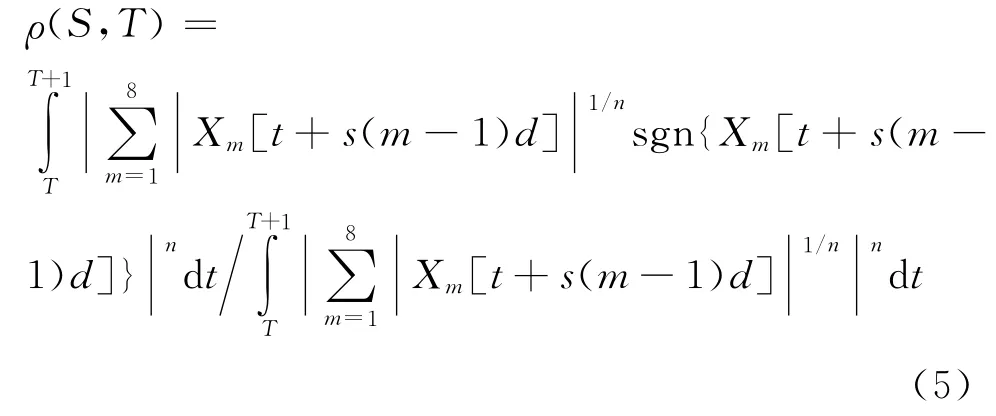
式中，S是慢度；T是对比窗口的起始位置；m是总的接收器数目；t是对比窗口长度；Xm（t）表示第m道声波信号；d表示声波间距。

2 反射纵波的产生及特点

在XMAC测井的全波列中，反射纵波一般具有以下特点［2］。

（1）反射纵波速度大于或接近地层滑行纵波速度，说明该反射纵波来自于地层内部，属于体波；

（2）反射纵波幅度比较小，在实测全波列波形中常常难于直接观测到；

（3）反射纵波到达时间大于纵波首波到时，而小于横波首波到时，并且在时间轴上延续很短。

3 实际全波列波形处理

图3为实际测量的某一深度段的共源距全波列波形。图3中直线标注出了存在比较明显的反射纵波，选取其中1个深度点的数据采用本文所提的方法进行研究。

图4为所选深度点的全波波形，由上到下依次为8个不同源距的接收器接收到的8道波形，组成共炮点道集，明显观测到斯通利波，纵波和横波幅度较小，观测不到反射纵波。图5为图4中波形的慢度－时间相关图，可以看出，原始的波形进行STC处理后，只有斯通利波表现出较好的相关性，在相关图中，很难确定其他模式波的慢度－时间区域。

图3 某一深度段共源距全波列波形

图4 共炮点实测声波全波阵列波形

对图4中的8道波形分别进行双树复小波变换，选取尺度4，进行4级小波分解，再通过单尺度小波重构，得到不同尺度上的重构波形，相同尺度上的波形组成共尺度道集。通过对不同尺度上共尺度道集的观测，发现在尺度3的共尺度道集上显示出比较明显的反射纵波，在源距较远的6道波形上可观测到明显的反射纵波（直线标注）。

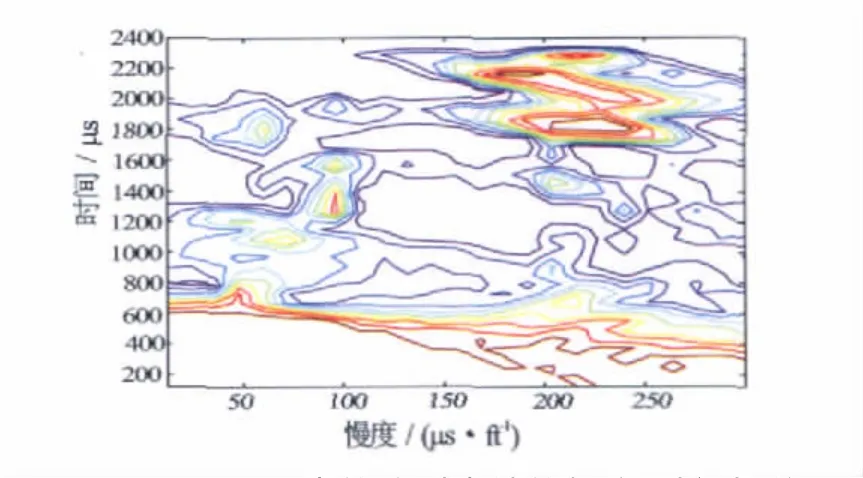
图5 图4中的阵列声波的慢度－时间相关图

图6 尺度3上的重构波形

由图6可以看出，虽然反射纵波比在原始波形下更明显了，但由于频率接近，在该尺度上依然存在纵波、横波等多种模式的波，通过多尺度方法还难以实现反射纵波的完全提取。

由于小波变换保留了时间域的特征，利用这一特点可以将慢度－时间相关法与多尺度相结合，用STC法对尺度3上的共尺度道集（见图6）进行处理，得到慢度－时间相关图。图7中，相关性较好的模式波为纵波、反射纵波和横波，其在图7中的区域分别为［40，70］×［300，900］、［20，60］×［900，1 200］、［80，110］×［1 200，1 800］，同时也计算出了反射纵波的慢度为36μs／ft（非法定计量单位，1ft＝12in＝0.304 8m，下同）。根据所确定的反射纵波的区域，即可得知在第1道波形上反射纵波的时间段为900～1 200μs，结合已经得到的慢度值即可计算出其他波形道上反射纵波的时间段。保留所确定的反射纵波时间段内的小波系数值，时间段外的小波系数值置0，就得到了最终要提取的反射纵波（见图8）。

用多尺度-STC方法处理了某一深度段的全波波形，图9为某一深度段共源距的全波波形处理结果。

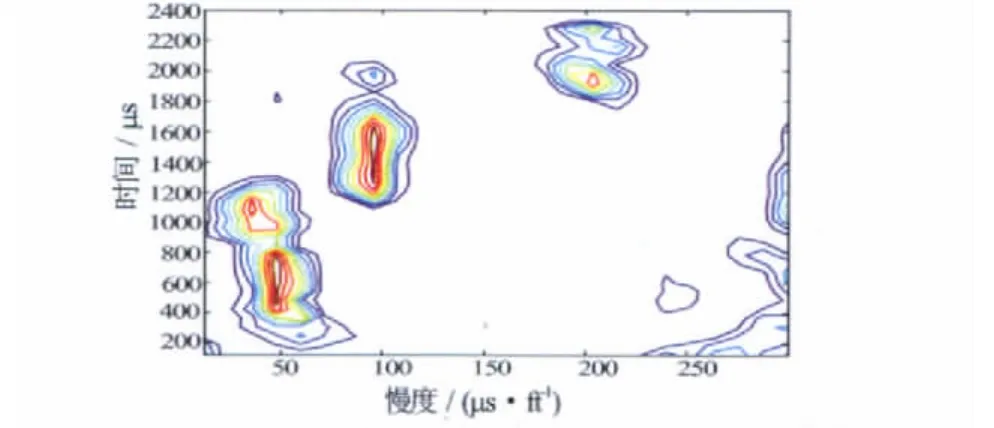
图7 尺度3下的共尺度道集的慢度－时间相关图

图8 反射纵波

图9 某一深度段共源距的反射纵波

4 结 论

（1）小波变换具有在时间域和频率域对信号进行局部化的特点，双树复小波克服了传统离散小波变换不具有平移不变性和方向选择性的缺陷，对于非平稳离散信号的处理具有更好的优势。

（2）基于小波的多尺度分解中尺度对应频率，根据不同模式波的频率特性，能够将全波信号中不同模式的波分离在不同的尺度上，在合适的尺度上重构波形，能够达到压制频率相差较大的高能量模式波，提取低能量信号的目的。

（3）小波变换很好地保留了时间域的特征，能够将STC与小波变换相结合。对不同尺度上重构的全波列进行STC处理，在得到的慢度－时间相关图上能够很好地确定相关性好的模式波的区域，进而对频率接近的模式波在时间上进行了分离。

（4）通过多尺度慢度－时间相关法对全波信号在频域和时域分别进行处理，达到了反射纵波的完美提取，为小信号的提取提供了一种新的方法。

［1］ 周继宏.探测井附近裂缝及其中流体性质的实验初探［J］.测井技术，1999，23（1）：6-8.

［2］ 邵维志，王晓杰，迟秀荣.用PP波识别井旁裂缝技术在碳酸盐岩地层中的应用［J］.测井技术，2001，25（5）：369－372.

［3］ 李长文，余春昊，赵旭东，等.反射波信息在裂缝储层评价中的应用［J］.测井技术，2003，27（3）：198－202.

［4］ 何峰江.声反射成像测井仪器仿真及波形处理技术研究［D］.北京：中国石油大学，2005：57－77.

［5］ 孙卫涛，陶 果，杨慧珠，等.基于多尺度分析的正交偶极子声波测井反演地层各向异性［J］.中国石油大学学报：自然科学版，2003，27（1），23－28.

［6］ 周曲曼，章成广.小波变换在声波全波测井处理中的应用［J］.石油天然气学报，2007，29（3）：231－233.

［7］ 段竹文，马英卓，黄庆程.提取全波列声波测井信号波前的一种新方法［J］.哈尔滨商业大学学报：自然科学版，2002，18（6）：635－643.

［8］ 宋延杰，何英伟，石 颖，等.慢度－时间相关法与遗传算法结合提取阵列声波时差［J］.测井技术，2006，30（2）：122－125.

［9］ Nick Kingsbury.Complex Wavelets for Shift Invariant Analysis and Filtering of Signals［J］.Journal of Applied and Computational Harmonic Analysis，2001，10（3）：234－253.

［10］Kingsbury N G.The Dual－tree Complex Wavelet Transform：A New Technique for Shift Invariance and Directional Filters［C］∥Proceedings of 8th IEEE Digital Signal Processing Workshop，Bryce Canyon，Utah，USA，1998：86－89.

［11］石宏理，胡 波.双树复小波变换及其应用综述［J］.信息与电子工程，2007，5（3）：229－234.