基于深度优先遍历算法的配电网拓扑动态检测

胡 荣,未召弟,符 杨

(上海电力学院电力与自动化工程学院,上海 200090)

配电系统自动分析是配电管理系统(DMS)的重要功能,其主要内容包括配电网的拓扑分析、潮流计算、可靠性计算、结构优化或网络重构、故障定位隔离与恢复等.网络拓扑分析功能解决配电网电气拓扑的建模问题,是其他高级功能的基础［1,2］.在进行结构优化、网络重构、故障恢复操作时,各种开关状态组合会产生多种拓扑结构,不仅会出现孤岛,而且可能出现环路.因此,需对两种情形进行判断,确保生成配电网辐射状网架,以寻找满足目标函数最优的网架结构.根据图论概念,将配电网拓扑结构视为无向图.目前多数文献［3-5］采用邻接表来存储无向图,物理模型不够直观,文献［6］采用矩阵染色法对拓扑结构仅作连通性分析.本文采用邻接矩阵存储方法和深度优先遍历算法,动态检测网络拓扑模型.

1 配电网络拓扑结构的对象描述

1.1 配电网络拓扑结构的数学模型

建立实用模型,实现图模一体化,是网络拓扑分析功能的关键.配电网络拓扑结构类似于一种数据结构——图.根据有关图论知识,配电系统拓扑结构图可表示为:

式中:V—— 包括电源、负荷侧配变在内的 n个节点的非空集;

D—— 边的集合(配电网馈线集合).

如图 1所示,当两节点的连接不涉及方向关系时,图为无向图,配电网络拓扑图为无向图.当两节点之间存在边(有连接关系)时,两节点互为邻接点,对应边用(V1,V2)表示.对于无向图,若每对节点之间都有路径直接或间接相通,则该图为连通图.因此,无向图 1为连通图.

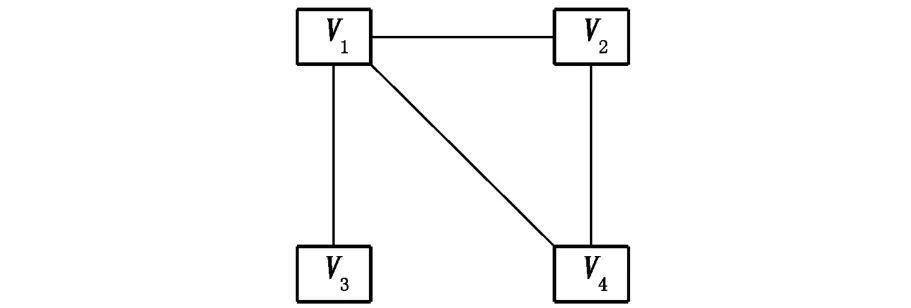
图1 图状结构G

从逻辑结构看,图是一种非线性结构,任意两个节点都可能存在关系,因而图的存储方法也有很多.本文采用更直观形象的邻接矩阵存储方法,利用网基结构矩阵 Dn×n作为邻接矩阵来描述配电网拓扑结构,以及取决于配电线路的架设、线路开关的状态和网络运行方式的配电网的潜在连接方式［7］.若图 1代表某一小型配电系统,则其网基结构矩阵为:

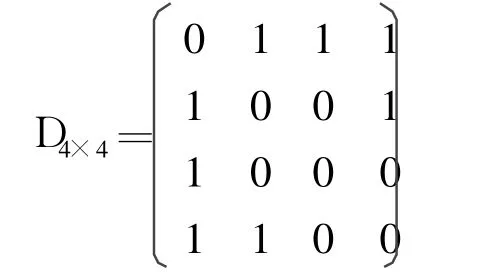
在配电分析系统中,配电网拓扑结构信息经DSCADA系统实时采集并传递给 GIS动态生成,其网基结构矩阵 Dn×n随拓扑结构的变化而动态变化,因此需要快速有效的算法进行动态检测,实现结构优化、故障定位和隔离,以及供电快速恢复等高级功能.

1.2 配电系统拓扑结构中的孤点和环路

配电系统多为环网设计,开环运行.每个用户终端原则上必须备有双侧电源,一侧电源在正常运行方式下对负荷供电,另一侧作为紧急备用电源.配电网的这种设计及运行方式决定了配电网拓扑结构图中除源节点之外的每个节点都有且只有一个父邻接点.若配电网络不连通,即某节点没有父邻接点,意味着此负荷点没有电源供电,称之为孤岛;若某节点有两个或两个以上父邻接点,说明此负荷节点有多个电源,称之为环路.

配电网环路有 2类［8］:一是 2个电源节点之间形成的环路,即从配电网的一个电源节点出发,每个节点只经过一次,到达本电源点或另一个电源节点的环;二是负荷节点之间形成的环路,即从配电网的某一个节点出发,每个节点只经过一次,又回到这个节点的环.配电网正常运行拓扑结构中一般不允许出现孤岛及环路.

文献［6］对配网拓扑结构作出连通性判断,但未对环路作出分析.本文将基于图状配电网拓扑结构,采用高效算法实现配电网拓扑结构的孤岛和环路的动态检测功能.

2 DFS算法在配电网拓扑结构动态检测中的应用

为尽快找到最优目标函数(网损最小、可靠性最高等)的网络结构,需淘汰拓扑结构不正常的网架结构.深度优先遍历算法(DFS)是一种人工智能算法,能够自动寻优.其优点是占内存较少,通常情况下可不必完全遍历即能找到最优方案或接近方案,以节省计算时间,提高计算效率.

2.1 DFS算法原理

DFS算法进行遍历的过程是从某个顶点出发,沿着某条搜索路径对图中每个节点各做一次且仅做一次访问［9］.原理如下:设 x是当前被访问节点,对 x做过访问标记后,选择一条从 x出发的未检测过的边(x,y).若发现节点 y已访问过,则重新选择另一条从 x出发的未检测过的边,否则沿边(x,y)到达未曾访问过的 y,对 y访问并将其标记;从 y开始搜索,直到搜索完从 y出发的所有路径,即访问完 y所有子节点之后,才回溯到节点x,再选择一条从 x出发的未检测过的边.上述过程直至从 x出发的所有边都已检测过为止.此时,若 x不是源点,则回溯到 x的父节点,直至图中所有和源点有路径相通的节点(即源点的所有子节点)都已被访问过.若图 1是连通图,则遍历过程结束,否则继续选择一个尚未被访问的节点作为新源点,进行新的搜索过程.

2.2 配电网拓扑结构动态检测的机理分析

电源点是配电网潮流首端,因此从电源点开始逐个遍历,进行标记,依次遍历其邻接点.若遍历中搜索到其他电源点,或某负荷节点被访问 2次,即可判断拓扑结构中存在环路;若遍历过程结束,仍有某负荷节点不曾被访问,则此负荷点为电源孤立节点;若遍历结束后未发现孤点或环路,说明配电网拓扑结构为正常运行的辐射、开式网状.

为使 DFS算法能够快速高效检测动态网络拓扑结构,设置数组 visited［0,1,…,n-1］及环路判断向量 path如下.

(1)数组 visited［0,1,…,n-1］的设置 由于图中任一节点都可能与其他节点邻接,在访问了某节点之后,可能顺着某条回路再次回到该节点.为了避免重复访问同一个节点,必须标记每个已访问的节点.为此,可设一数组 visited［0,1,…,n-1］,visited［i］的初值为 0,一旦访问了节点 i之后,将其置为 1.

(2)环路判断向量 path的设置 向量path记录已访问过且有可能产生环路的点,path［i］的值随程序的进行会不断变化,其原则是:访问到某点后即将其放入 path中,若判断完该点所有邻接节点且没有回路时,将该点从 path中删除.

(3)动态检测配电网络拓扑结构图的主要步骤 具体步骤如下.

第 1步 首先选取某个电源节点作为当前节点 i(1≤i≤n),把 visited［i］置为 1,表示该点已被访问,并将 i放入堆栈 path中.

第 2步 从 0～N中依次取当前点 i的各级邻接点 j,如果 j为另一电源点则说明存在一类环路;如果 j已被访问过且 j不是当前节点 i的父节点,则说明存在二类环路;如果出现以上两种情况中的一种,则程序记下环路,然后逐层退出递归,反之则把 j作为当前节点重新进行深度优先遍历.如果 j≥N则说明当前节点的所有连通节点已被处理完,此时把当前节点 i点从 path中移除,返回递归上一层.

第 3步 若上述判断未发现环路,取出下一个电源点重复第 2步.

第 4步 判断完所有电源点后,由所有的visited［i］统计从来没有被访问过的节点,若有,标记所有孤点,否则该拓扑结构一切正常.配电网络拓扑结构的动态检测流程见图 2.

图2 配电网络拓扑结构的动态检测流程

根据流程图编写程序对配电网络拓扑结构进行动态监测,可以剔除存在孤岛和环路的结构,以进一步提高配电网网络重构、故障恢复,以及寻找网损最小、可靠性最高的网架结构的效率,并将检验结果以可视化界面给出,将核心算法封装为模块供高级功能调用,从而进一步提高计算效率.

3 算例应用

在配电网 GIS能够直接读取 DSCADA中的实时数据的前提下,只有配电网自动分析系统能够辨识正常与非正常动态网络结构,进行潮流计算、网架结构优化、可靠性计算,才有现实意义,才能构建强大的配电网系统.

本文采用邻接矩阵的形式表示配电网络拓扑结构图,深度优先搜索(DFS)算法进行图的遍历和搜索,编写了“配电网拓扑结构动态检测”程序.为增强直观可视性,利用 VC++6.0编程工具,实现了友好的人机交互界面,并将核心算法封装为独立模块,以便潮流计算、网络优化或重构等高级功能软件的调用.图 3为典型的复杂配电网［10］,此网架结构中有 4个电源节点 S1,S2,S3,S4,50个负荷节点(1～50),实线表示原始线路,虚线表示可运行的线路.

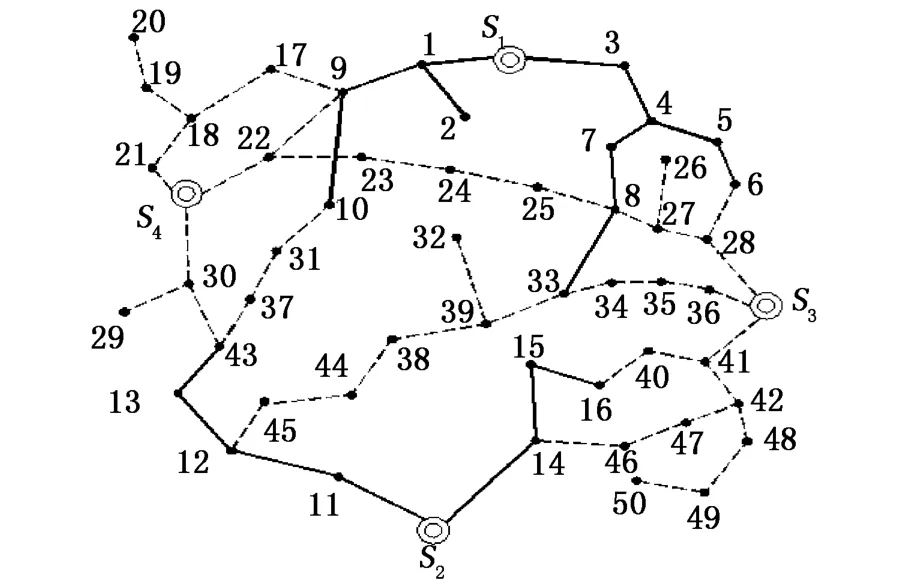
图3 典型的复杂配电网

分别对其各种非正常拓扑结构进行动态检测,如图 4所示.界面中给出了各种配电网拓扑结构的检测信息,对部分故障的负荷节点进行标记(方框显示).

由图 4a中的“检测信息”可知,此复杂配电网中负荷节点 38为孤点,即无电源对其进行供电.由图 4b中的“检测信息”可知,此配电网结构中负荷节点 11,12,45,44,38,32,39,33,34,35,36为双向电源供电,构成了一类环路.图 4c给出了二类环路的非正常拓扑结构,由“检测信息”可知,11,12,45,44,38,15,14显示均由电源 S2供电.

图4 非正常拓扑结构

为了验证程序的运行效率,采用文献［10］至文献［12］的算例给出的网架结构进行计算速度测算和正确率检验.对 3个算例可能出现的各种孤岛和环路情况进行的 600次试验表明,程序平均计算时间小于 1 ms,正确率达 100%,见表 1.

表1 程序运算效率验证结果

由表 1可知,程序计算速度及稳定可靠性均达到较高水平,完全可以高效地为配网重构、故障恢复提供可信赖的网络拓扑结构,检验结果验证了涉及的思想、采用的方法的合理性与优越性.

4 结束语

本文利用图状结构进行配电网络拓扑建模,采用深度优先遍历算法进行快速动态检测,编程采用 VC++6.0软件,建立了图形用户界面;将程序封装为模块,便于网络重构或故障恢复等高级功能软件的调用.通过算例演示及软件测试,验证了软件的正确性与优越性.

［1］顾秀芳,关长余.配电网潮流计算的拓扑分析研究［J］.华北电力大学学报,2008,35(2):47-50.

［2］张宏,郭宗仁.基于节点—— 支路关联矩阵的配电网馈线故障区域定位算法［J］.电力自动化设备,2004,24(1):27-29.

［3］马志刚,基于遗传模拟退火算法的配电网重构研究［D］.南昌大学,2006.

［4］邱生,张焰.用邻接表保存中压配电网拓扑结构［J］.电力自动化设备,2005,3(3):57-59.

［5］王林川,潘文明,梁栋,等.一种基于邻接矩阵的算法在配电网重构中应用［C］∥电力系统与自动化专业第 24届学术年会论文集,2008:367-369.

［6］崔岩.邻接矩阵染色法及其在电力系统网络拓扑分析中的应用［J］.电力系统保护与控制,2008,36(16):52-56.

［7］刘健,毕鹏翔,杨文宇,等.配电网理论及应用［M］.北京:中国水利水电出版社,2007:7-12.

［8］杨建军,战红,刘扬.基于环路和改进遗传算法的配电网络重构优化［J］.高电压技术,2007,33(5):109-113.

［9］SAHNISartaj.Data structures,algorithms,and applications in C++［M］.Beijing:China Machine Press,2004:98-105.

［10］VLADIMIRO,MIRANDA,RANITO JV,etal.Genetic algorithms in optimalmultistage distribution network planning［J］.IEEE Trans on Power Systems,1994,9(4):1 927-1 933.

［11］MORADI Adel,FOTUHI-FIRUZABAD M.Optimal switch placement in distribution systems using trinary partic le swarm optim ization algorithm［J］.Trans.on Power Delivery,2008,23(1):271-279.

［12］W ATANABE Isamu,NODU Makoto.A genetic algorithm for optim izing switching sequence of service restoration in distribution systems［C］∥Proceedings of the 2004 Congress on Evolutionary Computation,2004:1683-1690.