基于节点分离Lagrange有限元方法的超高速碰撞碎片云数值模拟＊

张晓天，贾光辉，黄 海

（北京航空航天大学宇航学院，北京100083）

1 引 言

超高速碰撞数值模拟技术是带有破碎环节的冲击动力学数值模拟方法的重要应用。超高速碰撞问题的特点是冲击速度快、材料变形大且破碎程度大，碎片往往以云状出现，具有高度非线性。

冲击动力学数值模拟方法主要包括Lagrange有限元方法、SPH 无网格方法和Euler有限元方法。传统Lagrange有限元方法在模拟大变形和破碎问题中会产生严重的网格畸变，使得计算难以进行。断裂侵蚀机制用删除大变形单元的方法解决了网格畸变的问题。但是在超高速碰撞问题中，由于变形区域较大，会有大量的单元被删除。这妨碍了破碎数值模拟中碎片的形成，难以模拟碎片云的演化。另外，冲击动能以势能的形式存入大变形单元中并进一步传播，删除大量单元的同时使得系统总能量大幅损失，造成变形模拟的失真，如图1。SPH 方法利用离散的粒子群模拟连续的物质，使用无网格技术解决了网格畸变问题，在碎片云模拟方面有突出的优势［1－2］，是目前使用最广泛的超高速碰撞数值模拟方法。但是SPH 方法由于要进行粒子搜索，计算效率低于有限元方法［3］。同时，该算法的受拉不稳定性会影响结果的准确度［4］。由于使用无网格技术，物质边界不明确是SPH 方法的又一不足。Euler有限元方法使用空间网格，网格不随物质变形而变形，因此不存在网格畸变问题，冲击模拟计算可以有效进行，但是同样难以刻画物质边界。鉴于现有方法仍存在不足，不断改进现有方法和探索新的思路仍是冲击破碎模拟算法研究的热点。

本文中，对Lagrange有限元方法进行改进，用节点分离方法和畸变侵蚀方法分别解决断裂机制问题和网格畸变问题，以替代断裂侵蚀机制。

图1 Lagrange算法算例［1］Fig.1 Asimulation example of the Lagrange method［1］

2 节点分离方法原理

节点分离方法是对传统Lagrange单元的一种改进，它将节点按参与构成的单元的个数进行复制，为这些单元各分配一个空间位置上重叠的节点，然后用断裂准则对所有空间位置重叠的节点族分别“捆绑”（约束相对自由度），当某节点的力学状态满足断裂准则时，此节点所在节点族解离，两两节点间不再传力，以此方式来描述材料的断裂特性。

节点分离方法由有限元前处理中的模型节点复制、初始约束添加和计算中的约束解除等3个步骤组成。

图2给出了一个前处理阶段进行模型的节点复制的示意图。首先，建立一般的Lagrange有限元网格，然后将节点N 复制为N1、N2、N3、N4，分别分配给共用节点N 的4个实体单元。然后，为新创建的4个节点添加约束，使之拥有一致的自由度。4个节点真实的空间位置是重合的，图2中人为将4个节点分离开来，只为方便表达。

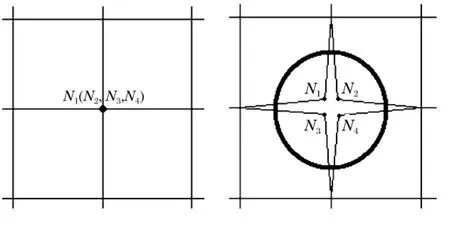
图2 节点复制Fig.2 Replication of nodes

3 畸变侵蚀方法

节点分离概念解决了网格断裂的问题，这是断裂分析的基本——断裂机制，但是Lagrange有限元网格在大变形下发生畸变的弊端并未解决。传统的Lagrange有限元断裂算法使用断裂侵蚀机制，将满足断裂条件的所有单元删除。这种做法一方面实现了网格断裂，另一方面处理了畸变单元。节点分离概念将满足断裂条件的节点组分离，并不删除单元，但是网格畸变并没有解决。畸变侵蚀方法根据单元当前的几何形状判断是否发生畸变，并将满足畸变判别准则的单元删除。由于六面体单元的计算精度高于四面体，本文的讨论仅限于六面体单元。单元畸变分为3种模式：单向尺度异常增大（模式A）、体积异常增大（模式B）和自穿透（模式C），见图3。

（1）畸变模式A 的判别

将一个六面体单元的8个节点分别向惯性坐标系投影，得到每个节点的坐标。畸变判别准则为

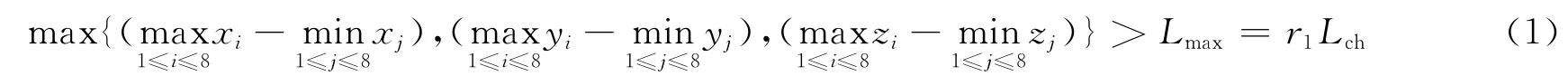
式中：Lmax为单向尺度阈值，Lch是划分网格时给定的单元特征长度，r1是单向增大阈值系数。如果沿某个惯性系坐标轴方向投影尺度超过此阈值，则认为该单元发生畸变。

（2）畸变模式B的判别

求解某时刻某1个单元在惯性系3个坐标轴上的投影尺寸，进而将3个投影尺寸的乘积作为当前单元体积的简化度量。如果满足下式，则认为该单元发生畸变

式中：r2为体积扩大倍数阈值。

（3）畸变模式C的判别

对于网格自穿透问题，需要判断某1个单元在任意1个节点处是否发生自穿透，如果有1个节点处发生，则认为整个单元发生畸变。如图4所示（图中节点对应关系见图3）。

对于节点B 来说，初始时相连的3条边为BA、BC、BF。令3个坐标轴与3条边固连，可以建立右手笛卡尔坐标系B－ACF，3个基矢量记为｛e1，e2，e3｝。在冲击过程中某时刻，该坐标系的3个基矢量在惯性系O－xyz 中的坐标形式可以由节点坐标定量计算得出，记为。该坐标系一般来说是笛卡尔斜角坐标系。由于惯性系是单位正交直角坐标系，因此这个斜角坐标系相对于惯性系的坐标变换矩阵Jacobian就是由单位正交基到｛e＇1，e＇2，e＇3｝的变换矩阵。而Jacobian的行列式值则反映了斜角坐标系B′－ACF 各基矢量之间耦合的程度。耦合程度越大，说明角变形越大。如果Jacobian的行列式值由正变负，则说明该坐标系由右手系变为左手系（图4中即是），这是由于节点F 穿透了面ABCD 造成的，即发生了自穿透。按此方法遍历该单元的所有节点，即可判断整个单元是否发生了自穿透。

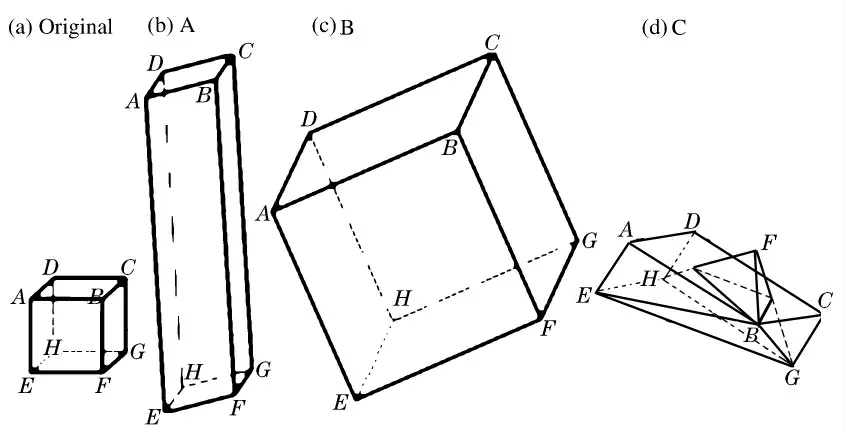
图3 六面体单元的3种畸变模式Fig.3 Three distortion modes of hexahedron elements

图4 网格自穿透的判别Fig.4Judgment of mesh self－piercing

将3种畸变模式综合，某单元只要发生了其中1种，即认为该单元发生畸变，予以删除。由于单元畸变的变形程度要大于单元断裂时的变形程度，所以使用节点分离方法加畸变侵蚀方法虽然与断裂侵蚀方法一样要删除单元，但是删除的数目要少很多，保留了那些大变形但未畸变的单元，保留了系统能量，在常规网格密度下可以提高计算结果的真实性。

节点分离只是一种有限元断裂数值模拟的概念，关于这种概念应用的文献较少，实现这个概念的具体技术途径也不尽相同，对应了不同的具体方法。有将节点分离概念用于模拟低速撞击、膨胀破裂和侵彻问题的［5－7］，但还没有将节点分离方法用于超高速碰撞数值模拟的。

4 节点分离方法基于LS－dyna的软件实现

本文中使用C＋＋编程调用LS－dyna求解器的技术途径实现节点分离算法。首先，使用通用有限元软件建立原始有限元网格。然后，通过自编程对原始网格进行节点复制、节点集建立和约束添加，并通过添加材料、接触、时间步、输出等LS－dyna的K 文件配置关键字生成节点分离方法的计算K 文件。之后，流程控制由自编程序来完成。在LS－dyna中，节点集的创建使用＊SET＿NODE＿LIST 关键字实现，而通过＊CONSTRAINED＿TIED＿NODES＿FAILURE 关键字实现节点集的约束和断裂应变阈值达到时节点集的自动解离。

程序调用LS－dyna求解器，进行显式积分计算至T 时刻终止，在求解结束后调用LS－prepost后处理软件读取d3plot计算结果，并将节点单元信息输出为文本文件。C＋＋程序读取文本文件中的计算结果数据，针对数据进行畸变侵蚀分析，确定要删除的严重畸变单元。程序创建LS－dyna重启动文件，将要删除的单元，按＊DELETE＿ELEMENT＿SOLID 关键字的格式写入LS－dyna重启动文件中，并将2T 作为下一个计算终止时刻写入重启动文件。之后再次调用LS－dyna求解器进行重启动分析，求解至2T 时刻终止，以此类推循环进行。流程如图5所示。

在这个流程中，节点分离模型的创建由通用前处理软件配合自编代码再辅助以人工完成，而使用自编程序调用LS－dyna频繁进行重启动分析的目的在于每隔T 时刻，停止计算并进行畸变侵蚀分析，删除严重畸变单元。而T 即为畸变侵蚀分析步长，这个步长并不需要等于LS－dyna求解器的显式积分步长，只要保证适时删除畸变单元保证计算正常有效进行即可。

图6给出了节点分离加畸变侵蚀方法对球形铝弹丸超高速撞击铝板的数值模拟算例，可见本方法具有碎片云模拟能力。

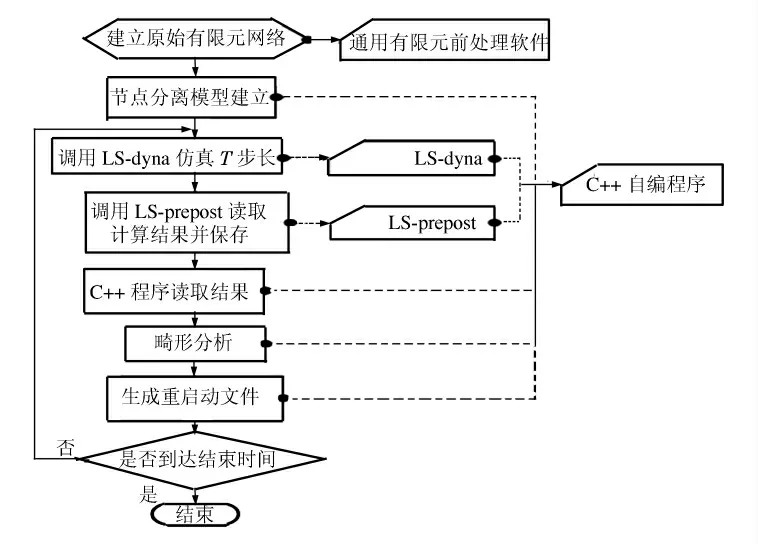
图5 计算流程图Fig.5 Computation flow chart

图6 节点分离方法碎片云Fig.6 Debris simulated by the node－separation method

5 实验验证

图7为文献［8］中的3层板防护结构超高速撞击实验的示意图。弹丸为Al 2024，防护屏均为Al 6061。弹丸直径7.9mm，撞击速度为5.5km／s，结构布局参数如图7所示。

使用节点分离的Lagrange有限元算法和SPH无网格算法对此实验进行数值模拟，并与实验结果以及手册中提供Euler有限元算法结果［8］进行对比。材料模型均为Johnson－Cook材料模型，材料参数见表1；状态方程为Gruneison状态方程，材料参数分别为［11］：γ＝1.97，c1＝5.386km／s，s1＝1.339，T0＝300K，c＝884J／（kg·K）。材料的断裂应变：Al 2024取0.8，Al 6061取1.0。

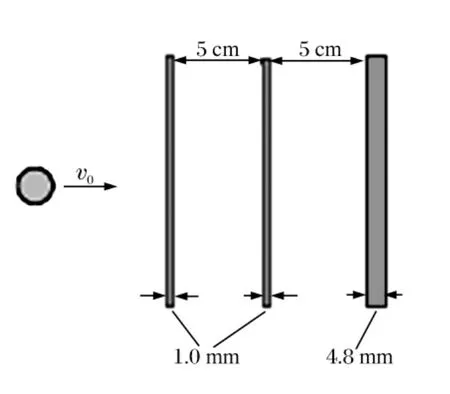
图7 实验工况Fig.7 Experiment configuration

表1 Johnson－Cook材料参数Table 1Johnson－Cook material parameters

图8为撞击后25μs时3种算法计算结果对比。其中，图8（a）为文献［8］中提供的Ouranos软件计算的结果，该软件基于Euler 2D 算法；图8（b）为本文中提出的节点分离加畸变侵蚀方法的计算结果；图8（c）～（d）为本文中使用LS－dyna的SPH 3D 算法的计算结果。在后3个算例中，均使用双CPU 并行计算。

表2给出了3层板穿孔情况、计算规模和计算时间。d1、d2为前、中板穿孔直径，ε1、ε2为误差。由穿孔直径可知，本文算法具有较高精度，明显优于Ouranos方法结果，略优于SPH－2结果。在同等计算规模（节点数目）下，本文方法和SPH 方法计算花费时间相当，但是本文方法结果明显优于SPH 方法。另外，SPH 方法的结果强依赖于粒子密度，SPH－2算例结果明显优于SPH－1结果且与节点分离方法精度相当；然而，SPH－2计算花费时间是节点分离方法的10倍以上。

图8 计算结果对比Fig.8 Comparison of results

表2 穿孔直径对比Table 2 Comparison of perforation diameters

6 结 论

提出了节点分离加畸变侵蚀的Lagrange有限元数值模拟方法，给出了基于LS－dyna软件的一种实现途径。使用该方法对超高速碰撞问题进行了数值模拟，与文献中的实验结果、数值模拟结果和SPH方法模拟结果做了对比，表明了该方法的可行性和有效性。

使用节点分离的Lagrange有限元方法模拟超高速碰撞问题，有效利用了Lagrange有限元方法的各种优势，如计算速度较快、稳定性好、物质边界明确等。因此，这种方法在超高速碰撞数值模拟方面，可以成为SPH 无网格方法的有效补充和替代。

［1］ 乐莉，闫军，钟秋海.超高速撞击仿真算法分析［J］.系统仿真学报，2004，16（9）：1941－1943.YUE Li，YAN Jun，ZHONG Qiu－hai.Simulations of debris impacts using three different algorithms［J］.Journal of System Simulation，2004，16（9）：1941－1943.

［2］ 贾光辉，黄海，胡震东.超高速撞击数值仿真结果分析［J］.爆炸与冲击，2005，25（1）：47－53.JIA Guang－hui，HUANG Hai，HU Zhen－dong.Simulation analyse of hypervelocity impact perforation［J］.Explosion and Shock Waves，2005，25（1）：47－53.

［3］ 王吉，王肖钧，卞梁.光滑粒子法与有限元的耦合算法及其在冲击动力学中的应用［J］.爆炸与冲击，2007，27（6）：522－528.WANG Ji，WANG Xiao－jun，BIAN Liang.Linking of smoothed particle hydrodynamics method to standard finite element method and its application in impact dynamics［J］.Explosion and Shock Waves，2007，27（6）：522－528.

［4］ Liu G R，Liu M B.Smoothed particle hydrodynamics：A meshfree particle method［M］.Singapore：World Scientific Publishing Company，2003：30－32.

［5］ Norman F K Jr.Comparison of two modeling approaches for thin－plate penetration simulation［C］∥6th International LS－DYNA Users Conference.Detroit，MI，USA，2000.

［6］ Lee M，Kim E Y，Yoo Y H.Simulation of high speed impact into ceramic composite systems using cohesive－law fracture model［J］.International Journal of Impact Engineering，2008，35（12）：1636－1641.

［7］ 高重阳.内部爆炸载荷下柱壳结构破裂问题的研究［D］.北京：清华大学，2000.

［8］ IADC WG3members.Protection manual（AI 20.1）［EB／OL］.Inter－Agency Space Debris Coordination Committee，2010－07.http：／／www.iadc－online.org／index.cgi？item＝docs＿pub.

［9］ Johnson G R，Cook W H.Selected Huguenots：EOS［C］∥7th International Ballistics.The Hague，Netherlands，1983.

［10］ Fish J.AL 6061－T6－elastomer impact simulations［EB／OL］.The Scientific Computation Research Center.http：／／www.scorec.rpi.edu／REPORT／2005－11.pdf.

［11］ 张庆明，黄风雷.超高速碰撞动力学引论［M］.北京：科学出版社，2000.