汽车起重机的整机结构分析技术研究

陈黎峰

（浙江省特种设备检验研究院，浙江杭州310020）

以有限元分析方法为基础的计算力学，经历了由简单到复杂、由线性到非线性分析的发展过程。结构分析要解决的实际工程问题，早已不是一个简单的零件或结构件，而是多个复杂结构件的组合结构，或整个产品的大型复杂问题。

1 对整体结构分析的回顾

作为结构的局部分析，必须引进局部的边界条件。但是，从结构总体受力来看，局部的边界条件往往使结构的实际传力状况发生扭曲，结构件之间的弹性连接变为了刚性连接，无法正确反映结构件之间的实际传力关系。利用结构的这种局部分析结果，评估结构整体受力后的结果，往往导致较大的误差。在工程设计中，局部分析不能替代整体分析，整体分析由于规模大、难度高，往往成为十分迫切与关键的瓶颈问题。但是，大容量、高速度计算机技术的发展，对整个产品进行结构分析，已经成为十分现实的问题了。飞机的整体求解，起重机的整体求解，都是这类大型复杂结构分析的典型例子。实际上，我国计算力学工作者在上世纪70年代末，采用多重子结构的超元矩阵方法[1]，成功地解决了飞机结构的整体分析问题；80年代，国外解决大型复杂结构分析的先进技术传到我国，MSC/NASTRAN系统的超单元技术[2]、ANSYS的子模型技术[3]，使许多大型复杂的结构分析问题变得简单容易。

2 整体结构的剖分与子结构分析

整体结构的基本特点，是结构规模大且组合形式复杂。目前，国际上解决大型复杂结构的分析问题，通常选择子结构方法，或者结构超单元方法。由于超单元实际上是子结构的一种表达形式，因此这里仅说明子结构分析技术。

对于任何一个大型复杂结构，总可以划分为若干结构件（简称为子结构），它们靠边界节点与整体结构相关连。如果将所有的子结构的边界节点组成一个集合，那么这个集合便表征了这个大型复杂结构的连接骨架，称之为边界结构。只要把各子结构对有关边界节点的刚度效应（或影响）计算出来，并施加在这些边界节点上，则解决大型复杂结构问题，转变为求解规模小得多的若干子结构及边界结构问题。

当然，如果边界结构与子结构的规模也可能很大，还可以再剖分为若干二级或三级的子结构。当然，这种多重子结构的使用，将带来分析流程的复杂化。因此，如何有效地剖分整体结构，便成了问题的关键所在。用K表示子结构的总刚度矩阵，U表示子结构的总位移矩阵，P表示子结构的总载荷矩阵；Ki、Kb、Kib表示与子结构内部和边界节点的相关的刚度矩阵；Pi、Pb表示与子结构内部与边界节点相关的外载荷矩阵；Ui、Ub表示子结构的内部与边界节点的相关位移矩阵。我们将有平衡方程

其中，

对子结构的分析，其主要计算工作量是消除该子结构的内部节点自由度，得到它的等效矩阵。从式（1）、式（2）可看出，如果各子结构的边界节点越少，则这些等效矩阵的规模也越小，最终的边界子结构的规模也越小，其运算速度也越快。因此，划分复杂结构为多个子结构的一个基本方法，就是要尽量控制子结构的内部节点规模适当，并且具有边界节点的数目较少。充分利用结构的链式、外伸等特点，合理划分子结构，可收到较好的效果。

3 子结构的变换与组装

在一般的整体结构分析中，使用了4种坐标系：总体坐标系，子结构坐标系，元素坐标系和节点坐标系。节点坐标系，确定了节点自由度的方向；元素坐标系，规定了元素刚度（载荷）矩阵与子结构之间的变换矩阵；子结构坐标系，将确定子结构等效边界刚度（载荷）矩阵向整体结构的组装的变换矩阵；整体坐标系，通常取世界系。

对于子结构分析来说，子结构的几何建模与应力分析是在子结构的局部坐标系下进行的。但是，子结构的等效刚度（载荷）矩阵，却必须按总体坐标系进行组装。因此，每一个子结构在组装之前，需要对等效边界刚度（载荷）矩阵进行坐标变换。我们设B为子结构对总体系的变换矩阵（通常它由整体系的3个结点确定：节点1定义原点，节点1-2方向定义X向，节点1-2连线与节点1-3定义连线构成的平面法线确定Z向，由Z与X向构成的平面法线定义Y向），则整个结构的边界子结构的刚度（载荷）矩阵为

给定整体结构6个刚体自由度的约束，求解式（7），我们将得到整体边界结构的位移。再经过整体边界位移向子结构的坐标变换，执行式（4），将求得子结构的内部节点自由度。

4 起重机整机分析的子结构技术

4.1 模型简化的基本准则

汽车起重机是多个结构件的组合，包含吊臂、转台、底架、支腿等结构件，以及回转、变幅、伸缩、起升等机构。在作业过程中，吊臂相对于转台，可以变幅与伸缩。而吊臂与转台的组合结构，可绕回转中心360°转动。因此，对整机系统的分析，不仅需要将所有的结构件及机构加以考虑，而且需要将作业过程中的不同载荷工况加以考虑。为了控制整机分析的规模，模型的建立既要尽量理想化、简单化、典型化，又要较客观地反映出整机（特别是结构件连接部位）的应力分布、变形（刚度）及失效等问题。汽车起重机最危险的工况，是起重作业工况，其传力路线是：重物→吊臂→变幅油缸支撑→转台→回转支撑→底架→支腿→垂直油缸→地面。

作业运动表明，吊臂的变幅、伸缩及吊臂与转台的组合结构的回转，对底架与4个支腿的结构变形与应力水平有较大影响，有必要选择多种典型的作业工况加以计算。同时，还要根据工程规范，考虑风载、惯性载、作业场地的不平等多因素对整机受力的影响。

整机系统的复杂性与控制分析规模的需要，整机模型的简化基于下述原则：确保整机的传力路线完整，确保整机典型作业工况的实用性，关键结构件的基本参数化，将整机分析与结构件分析紧密结合，对结构的细节结构作重要简化，整机有限元建模及分析流程自动化。

4.2 子结构的划分

为使整机分析与结构件分析能够结合进行，我们以结构件为基础划分子结构，突出三大结构件：吊臂、转台、底架。三大结构件之间的众多连接结构件，均作重大简化。

（1）吊臂的简化。首先，简化各节吊臂之间的连接结构及伸缩机构，吊臂简化为薄壁四边形或六边形盒体模型。为确保结构刚度，应注意变幅油缸支撑部分、根部与顶部的结构加强。吊臂的子结构坐标系的原点，取在吊臂根部转轴的中心，X轴沿臂体方向指向顶部，Y轴与地面平行，Z轴指向上盖板方向。这样，吊臂与整体系之间的转换矩阵，仅由两个角度确定：吊臂与地面的夹角α，转台绕Z轴的转角φ＋180°。若转台角φ等于0°，则吊臂顶部指向车的正前方。

（2）转台的简化。简化小回转机构为力矩，卷扬机构为横梁，钢丝纯为二力杆，配重为集中力，变幅油缸支撑的转轴及吊臂的转轴为横梁，回转支撑结构的上垫圈为曲梁，忽略纵向的斜支撑板及横向的某些连板，转台成为典型的薄壁组合结构。转台的子结构坐标系的原点，取在转台平台的回转中心点，XY平面与该平台平行。转台与整体系之间的转换矩阵，仅由转台的转角φ确定。

（3）底架的简化。整个底架是一个薄壁组合结构，将固定支腿与活动支腿作为底架的一部分进行延伸。考虑到最危险的工况是起重作业，汽车自重作为一个集中力加在车架上，回转支撑的下垫圈简化为曲梁。作为方案设计模型，沿下垫圈进行的结构加强也被忽略。为避免支腿油缸与地面的面接触计算，支腿油缸被简化为一个倒五面锥体结构，使起重机作业时能够仅4点触地，便于判断地面对支腿的接触反力。底架的子结构坐标系与整体系的完全相同。

（4）连接结构的简化。各结构件之间的连接结构作如下简化：吊臂与转台之间的变幅油缸支撑简化为抗压、抗扭、抗弯的梁单元，吊臂根部与转台支撑之间的转轴简化为梁，回转支撑的垫圈、滚珠与螺栓柱，用厚壳板元与梁单元模拟。

4.3 整机结构分析的自动化

（1）整机模型的参数化。整机模型的参数化，是以子结构参数化为基础的，子结构以关键结构件为实体。因此，结构件的参数化与整机的参数化，可以有机地结合起来，建立统一的结构参数库文件。

（2）结构件的宏程序库。结构件的模型自动产生程序，是以APDL语言为平台开发的，它将调用结构参数库文件的相关模块。只要一旦实现结构件的参数化，其几何模型自动产生程序便以宏子程序方式建立。这就构成了结构件几何模型的宏程序库。结构件与整机模型均调用宏程序库产生，有利于整机分析与结构件分析的协调，整机分析的某些结果，也可作为结构件分析的边界条件。

（3）整机模型的集成。集成结构件模型建立整机模型，变成了结构件模型的组装与连接。结构件的组装与连接，都必须在总体系下进行。第一步，要设置子结构坐标系，定义原点与坐标系方向；第二步，要调用相关结构件的宏子程序自动产生几何模型；最后，还要恢复总体系。

整机建模的难点，在回转支撑的模拟上。回转支撑结构的上下垫圈作为曲梁元，以分别包括在转台与底架模型中，参与转台与车架平台的抗弯。因此，转台与底架的连接，主要成为用厚壳元与短梁元模拟滚珠与螺栓柱的支撑连接。

（4）整机分析的基本步骤。综合上述，可对整机分析的基本步骤作一定的规范：建立以结构件为基本模块的参数库文件；以APDL为平台，开发结构件的宏程序库；调用宏程序库，开发整机模型的集成程序；建立整机的分析流程；建立后置处理流程。

4.4 整机分析在起重机QY25D的工程应用

QY25D是一个六边形四节臂的中吨位汽车起重机。整机划分为3个子结构，现已建立两个用于整机分析的程序：

（1）整机方案设计的有限元参数化模型产生程序。其主要功能，是对全机方案设计模型进行有限元分析。整机模型具有3 067个节点，shell63元素3 149个，beam4元素133个，link8元素1个，有效自由度为17 597。

（2）具有详细设计车架模型的全机有限元参数化模型产生程序。其主要功能，是对具有车架局部加强的整机设计模型进行有限元分析。整机模型具有4 367个节点，shell63元素4471个，beam4元素217个，link8元素1个，有效自由度为25 166。

方案（1）与方案（2）比较表明，模型节点网格局部细化，会使模型分析规模大。

图1、图2表明整机分析的应力分布云图。整机应力水平与分布的合理性，证明了本文介绍的方法的正确性。QY25D的4种工况的应力水平均在较理想的许用应力范围。但是，文献[4]表明结构件的局部稳定性，是值得十分重视的。

图1 整机分析的Von Misses应力云图

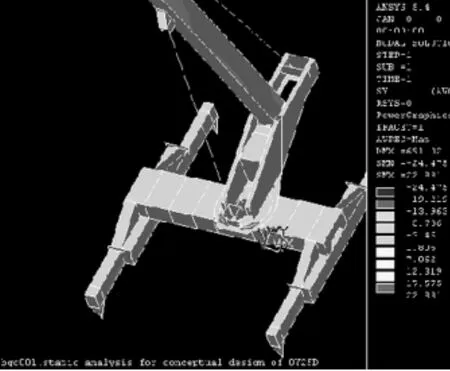
图2 整机分析的的Y向局部变形与应力分析云图

5 结束语

通过以上对汽车起重机的模型结构简化，较之以前的局部结构受力分析更加全面合理，其受力大大趋于合理安全，结构也比以前更加紧凑，节约了汽车起重机的制造成本。

[1]陈焕星.大型通用有限元结构分析系统MSC/NASTRAN用户手册[K].北京：中国飞机结构强度研究所，1989.

[2]刘鸿文.材料力学[M].北京：高等教育出版社，1993.

[3]王文斌.机械设计手册[M].北京：机械工业出版社，2007.

[4]杨达夫.金属结构设计[M].北京：水利电力出版社出版，1995.