转炉托圈的强度分析
李彦彦,李冠鹏
(河南城建学院土木与材料工程系,河南平顶山467036)
0 引言
目前,氧气顶吹转炉炼钢设备在钢铁行业中发挥着极为重要的作用。氧气顶吹炼转炉的本体系统由炉体、炉体支撑系统、倾动机构和扭矩平衡装置四部分组成,其结构示意图如图1所示。炉体和附件的全部重量通过支承系统传递到基础上,支承系统的部分构件还承担着传递从倾动机构到炉体之间的倾动力矩,实现炉体的转动[1]。因此,支承系统对转炉的运行状态有直接的影响。炉体支承系统主要包括托圈、托圈与炉体之间的连接装置、耳轴、耳轴轴承和底座。托圈是转炉的重要承载和传动部件。在工作过程中,托圈除承受炉体、钢液及炉体附件的静载荷和传递倾动力外,还承受频繁启、制动产生的负荷和由于炉体、钢水罐、渣罐、烟罩及喷溅物的热辐射、热传导所产生的热负荷。为确保转炉的正常运行,托圈应满足强度和刚度要求[1]。
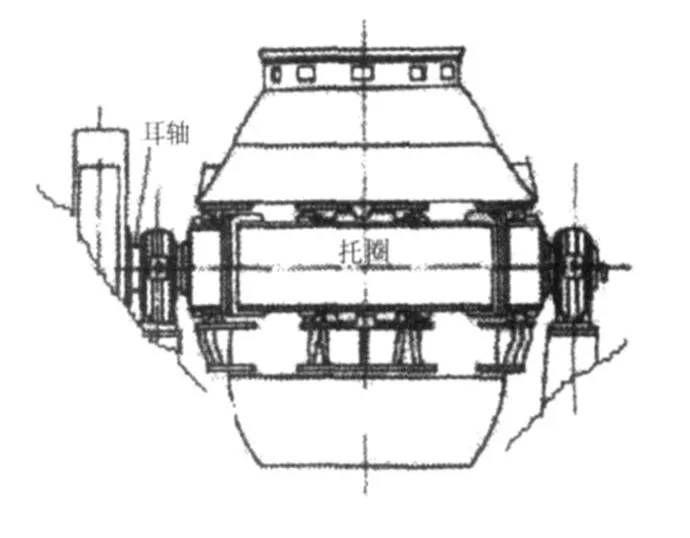
图1 转炉结构示意图
1 托圈的截面形式和外载荷的简化
托圈的断面形状有开口和闭口两种。闭口断面多为矩形,开口断面有C形和反C形。托圈断面一般采用钢板焊接的箱形(矩形)断面结构。在这种断面结构中,切应力在整个断面上均匀分布,并且矩形断面结构的抗扭刚度比开口断面的大很多倍。托圈是由四个部分所组成,即由驱动侧耳轴座、从动侧耳轴座、出钢侧托圈瓣和装料侧托圈瓣焊接而成[2]。
炉体通过三个垂直链杆和两个水平链杆连接在托圈上。两个水平链杆分别位于驱动侧耳轴和从动侧耳轴上,三个垂直链杆分别位于与托圈平面成45°、180°和315°的位置。炉体和载荷的全部重量Q通过托圈的支承点传递到托圈上。支承方式不同,托圈支承点的数目也会不同。如果支承点超过三点,炉体和载荷的全部重量在托圈上的载荷属于超静定问题[1]。转炉在转动的过程中,托圈平面的横向力通过水平链杆和固定支承向托圈传递,为计算方便,将链杆简化为二力杆。
当转炉转动α角后,作用在托圈上的外力有炉体及载荷的总重量Q(炉壳自重、炉衬重量、炉内金属和渣的重量、炉口粘渣及炉壳上的附件等)、炉体及载荷的反力矩MQ=QLα和耳轴轴承的支反力等。
忽略耳轴轴承的摩檫,根据平衡条件则有:

即炉体及载荷的反力矩MQ等于使转炉转动的倾动力矩Mα。
当转炉转动α角后,炉体及载荷的总重量Q在托圈上产生外力,在每个支承点上可分解为平行于托圈平面的载荷PH与垂直于托圈平面的载荷PV。为使问题简化,将这两个分力单独进行研究。平行于托圈平面的载荷包括沿托圈盖板平面的两个水平集中载荷,简化到托圈上的两个耳轴水平支反力和由轴承支承偏距引起的,水平支反力在耳轴与托圈连接点产生的弯矩。垂直于托圈平面的载荷包括两个垂直集中载荷PV,简化到托圈上的两个耳轴垂直支反力V和由支承偏距引起的,垂直支反力V在耳轴与托圈连接点产生的扭矩K。
炉体及载荷总重量Q在托圈上产生的外力,分解后各个力的大小分别为:

2 内力计算理论
当托圈受垂直于环平面的载荷作用时,内力计算的前提条件有两个:一是托圈圆环是回转体;二是托圈圆环横截面的主惯性轴之一位于环的中心线平面内。
如图2所示,托圈受垂直于环平面的集中载荷Pn、力矩Mi和Kj扭矩的作用。力矩Mi和扭矩Kj的矢量用双箭头表示,其方向由右手螺旋法则确定,规定角φ从0开始,顺时针方向为正。

图2 托圈受垂直于环平面的载荷简图

图3 托圈受平行于环平面的载荷简图
在分析圆环中的内力时,假想在φ=0处将圆环截开,在截面的左、右两侧作用的切向力、弯矩、扭矩分别用表示;在任意截面处φ, 圆环的内力用Q(φ)、Mx(φ)和MK(φ)表示。
如图3所示圆环,在平行于托圈平面内受到的载荷有集中法向力Pn、集中切向力Pj和力矩Mi,方向皆以图中标示的方向为正方向。规定角φ从0开始,顺时针方向为正。
3 空心矩形截面托圈的机械应力
托圈截面如图4所示,作用于托圈截面的载荷有轴向力N,切向力Qx、Qy,弯矩Mx、My,和扭矩MK。对于空心矩形截面,其外侧矩形的高为h,宽为b;内侧矩形的高为h1,宽为b1。在计算时忽略托圈曲率的影响,其应力有[3]:
⑴轴向拉应力与轴向压应力

⑵弯曲正应力


图4 托圈截面形状
在中性轴上切应力有最大值。
⑷扭矩MK所产生的切应力
当空心矩形截面的壁厚很小时,应用弹性力学薄壁管的扭转理论计算,其切应力为:当h>b时,最大扭转切应力在长边的中点:

短边中点的切应力为:

短边中点的切应力是短边上切应力的最大值。
4 托圈耳轴的强度分析
以120 t转炉为例介绍转炉托圈强度的计算,并用第三强度理论和第四强度理论进行对比,确定合理的校核方法。该托圈的外径为8 400 mm,内径为6 800 mm,空炉的重量为5 000 kN,炉水的重量为1 200 kN。分别采用第三强度理论和第四强度理论,结合前面介绍的理论,分别计算倾动角α=0°时、承受最大倾动力矩时和承受事故力矩时的最大应力,与许用应力比较,校核托圈尺寸是否满足要求。
以倾动角α=0为例,耳轴的受力简图如图5所示。
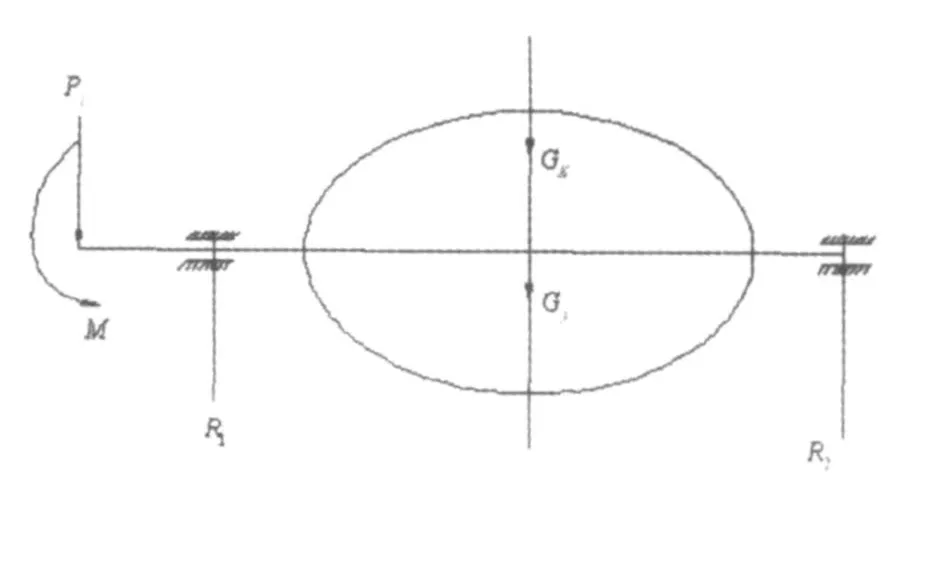
图5 耳轴的受力简图
通过第三强度理论计算出最大的应力为34.336 MPa,通过第四强度理论计算出最大的应力为31.239 6MPa,查机械零件设计手册[4]得Q345的许用应力[σ]=275 MPa,可见托圈强度满足要求。
采用同样的方法对其它两种情况进行计算,然后进行校核,校核后发现均满足强度要求。
5 结束语
通过以上计算可知,采用第三强度理论对转炉托圈进行强度校核,其准确度更高一些。通过与转炉实际工作过程中获得的最大应力进行比较,发现两者差距不大。因此,可以采用第三强度理论进行转炉托圈强度的分析。
[1] 谭牧田.氧气转炉炼钢设备[M].北京:机械工业出版社,1983.
[2] 罗振才.炼钢机械[M].北京:冶金工业出版社,1982.
[3] 刘鸿文.材料力学[M].北京:高等教育出版社,2004.
[4] 成大先.机械设计手册[M]:4版.北京:化学工业出版社,2002.

