内反馈斩波式串级调速控制系统研究与仿真

刘 岩,王兵树

(1.华北电力大学 控制与计算机工程学院,河北 保定 071003;2.华北电力大学 仿真与控制技术研究所,河北 保定 071003)

内反馈斩波式串级调速控制系统研究与仿真

刘 岩1,王兵树2

(1.华北电力大学 控制与计算机工程学院,河北 保定 071003;2.华北电力大学 仿真与控制技术研究所,河北 保定 071003)

根据内反馈斩波式串级调速双闭环系统的控制原理,分析并建立了内反馈斩波式串级调速双闭环控制系统的相关模型,并根据建立的模型,利用 Matlab/Simulink工具箱搭建了内反馈斩波式串级调速双闭环控制系统的仿真模型。仿真结果验证了加入双闭环控制策略后整个系统的性能得到了很好地改善。

斩波串级调速;双闭环控制; Matlab/Simu link

0 引 言

目前,内反馈斩波式串级调速技术已广泛应用于带风机、水泵等负载的异步电动机中,但国内工业现场所使用的内反馈斩波调速系统的斩波部分都是采用开环控制,这种控制方法不具备限流功能,容易产生过流保护,甚至烧毁设备。因此对于一些要求调速精度高、扰动大、调速范围大的负载,例如提升机,就需要一种具有更高准确性,更好抗干扰性和可靠性的控制方案。因此,为使现代串级调速系统能够满足不同负载的要求,对斩波部分采用双闭环控制方法是必要的。

1 内反馈斩波式串级调速原理

内反馈斩波式串级调速系统的原理如图 1所示。内反馈所指的是内反馈电机,它是利用电机绕组多重化技术,在异步电机的定子铁芯上增设了一套绕组,该绕组主要是用来接收从转子反馈回来的能量以实现电机调速。

图1中异步电动机转子输出电压接至三相桥式不可控整流器 UR,通过 IGBT直流斩波器与电源换相的三相桥式可控硅逆变器 UI相连。为了提高功率因数降低无功分量,把逆变器的逆变角设置为最小逆变角 βmin。当 IGBT斩波开关工作周期为 T,在 τ的时间里,斩波开关闭合,转子直流被短路而不流过逆变器,而在 T-τ的时间里,斩波开关断开转子电流被迫流入逆变器。整流桥的输出电压为：

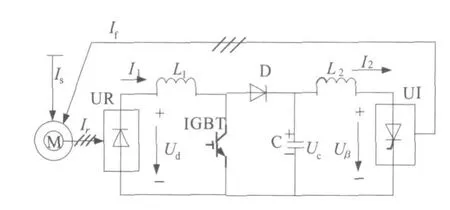
图1 内反馈斩波式串级调速系统原理图Fig.1 Internal feedback chopped cascade speed-control system diagram

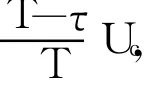
由式 (1)、 (2)、 (3)可以得到转速公式如下：

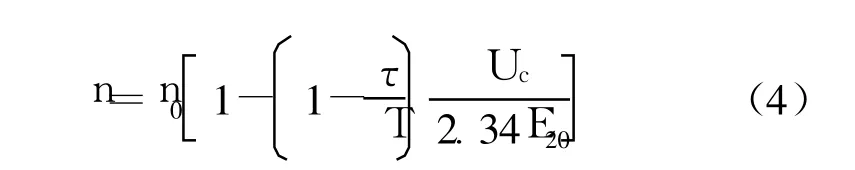
由式 (4)可见,改变斩波器开关闭合时间 τ的大小就可以改变电机转速 n的大小。从而转子转速便可以在设计的最低转速和额定转速间平滑的变化,达到平滑无级调速的目的[1]。

2 控制系统的设计

2.1 斩波直流回路数学模型

由图 1可知系统的主电路是一典型的升压斩波电路,其输入为转子整流电压和有源逆变侧的逆变电压。输出为流过两电感的电流以及电容电压。由文献 [2]可知斩波串级调速系统的主回路在连续导电模式下可以使用两个线性时变电路来表示,它们与一个开关周期中的两种开关状态分别对应 (如图 2、图 3)。

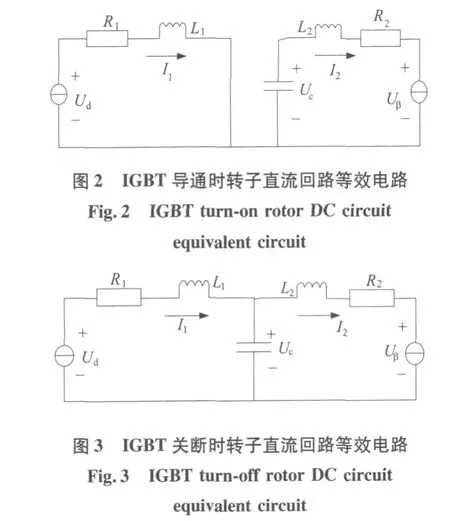
(1)在第k个周期当 IGBT导通时,导通时间为 t,tk≤t≤tk+dT,等效电路如图 2所示,此时回路的状态方程可表示为：

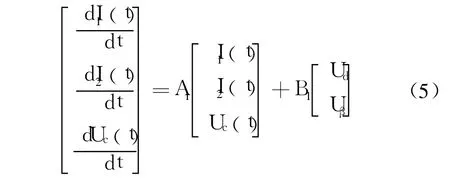
式中系数矩阵 A1和 B1分别为：

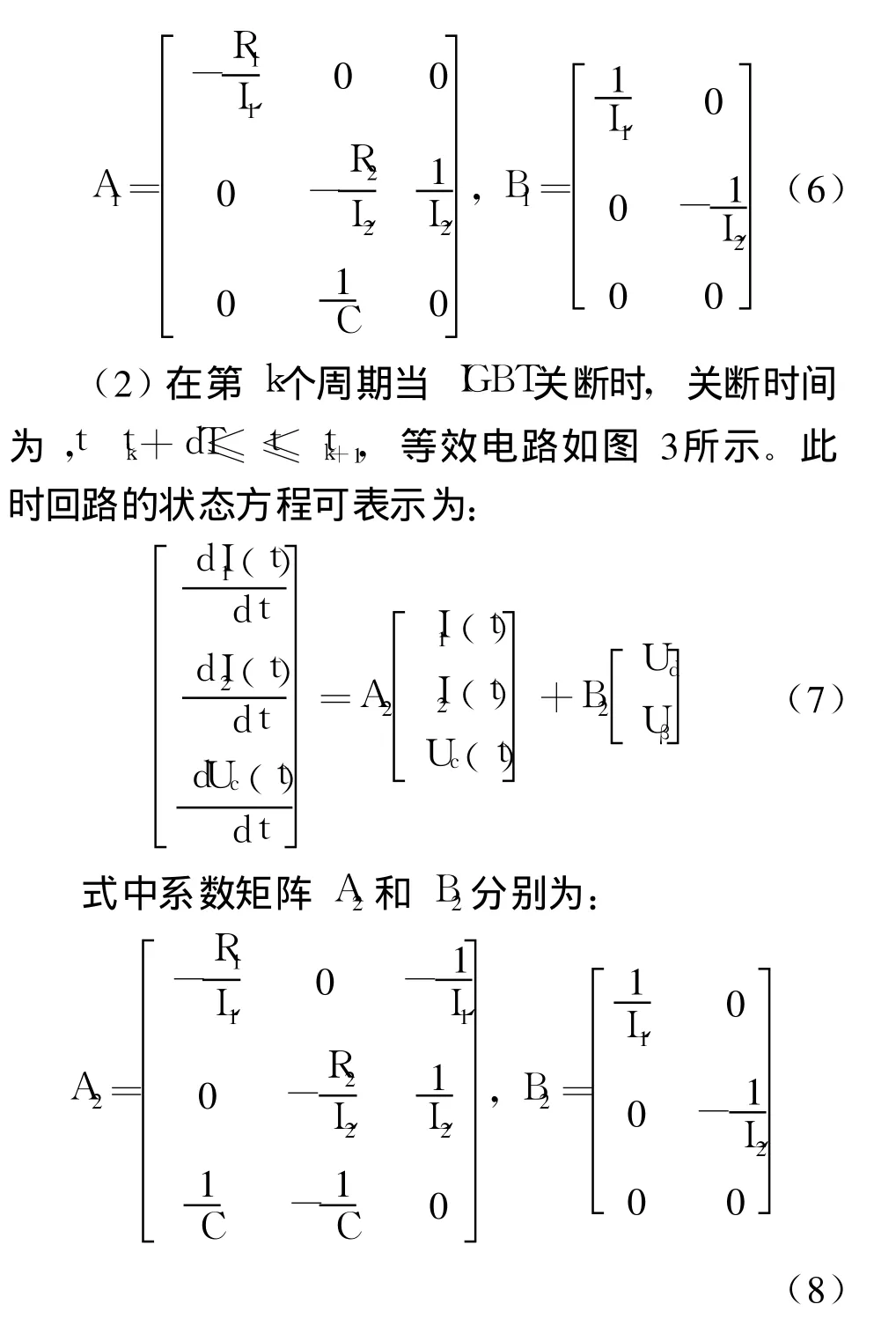
式 (5)、(7)为连续系统状态方程,由于系统状态变量电感电流和电容电压的连续性,可将第一个回路状态的终值作为第二个回路状态的初值,解这两个方程可得在第 k个周期中状态变量的解为：

转子整流电压和有源逆变电压分别为 Ud=2.34sE20和 Uβ=2.34ET2cosβmin。对上式的变量分别引入扰动量,在某一静态工作点附近进行泰勒级数展开并经过拉氏变换便可得到直流主回路的传递函数如下：

Id代表了一个斩波周期内负载直流电流的平均值;RD和 RT为折算到转子侧和逆变侧的等效电阻;XD和 XT分别为折算到转子侧和逆变侧的等效漏抗;R1和 R2分别为转子整流侧和逆变侧的线路电阻;s为转差率;TLi为转子直流回路的时间常数;KLi为转子直流回路的放大系数。

由于信号采样到 PWM,脉冲发出会有延迟,因此占空比的变换到直流母线电流发生作用还要存在一个载波周期的滞后,因为时间常数很小,一般看成一个一阶惯性环节,即

2.2 异步电动机数学模型

由文献 [3]可得内馈电机的运动方程为

式中： M为电机的电磁转矩; Mc为负载转矩;GD2为折算到电动机轴上的拖动系统之飞轮惯量。

最后从电机的电磁转矩方程及电力拖动的运动方程式可推导出内反馈电机的传递函数[3～7]：

式中：CM为转矩系数。

2.3 双闭环控制系统的设计

根据上述内反馈斩波串级调速各部分的传递函数建立系统的框图如图 4所示。

图4中 ASR与 ACR分别为速度环调节器与电流环调节器,为了使系统能得到良好的静动态性能,两个调节器均采用 PI调节器。同时根据系统要求对串级调速双闭环控制系统进行动态分析和校正,采用 “电子最佳调节方法”[2]对系统进行校正分析。由于电流环以跟随性能为主,应按典型Ⅰ型系统[8]进行设计。由于转速外环的主要作用是稳定转速,因此,速度环需要具有较高的抗扰动性可以按照典型Ⅱ型系统[8]设计转速调节器。

3 基于MATLAB/SI MULINK的双闭环串级调速系统的仿真与分析

利用 MATLAB/SI MULINK工具箱搭建了斩波式串级调速系统的仿真模型,该模型经过验证可以很好地模拟实际斩波式串级调速系统[8～11],并以额定功率 560 kW的内反馈电机,带平方转矩负载为实例,对整个斩波式串级调速系统进行了实验仿真。表1给出了从720 r/min分别下调至常用给定范围转速的超调量和调节时间。从表 1中可以看出超调量δ≤4.6%;调整时间 (2%误差带)ts≤1.8 s。图 5所示的直流电流、转速的波形为调整到给定转速 500 r/min时的动态过程。

表 1 额定转速调至常用给定范围转速的超调量和调节时间Tab.1 Overshoot and settling time at rated speedad just to different common speed

图4 斩波串速系统双闭环控制动态结构图Fig.4 Dynam ic structure o f Chopper speed doub le closed loopcontrol system

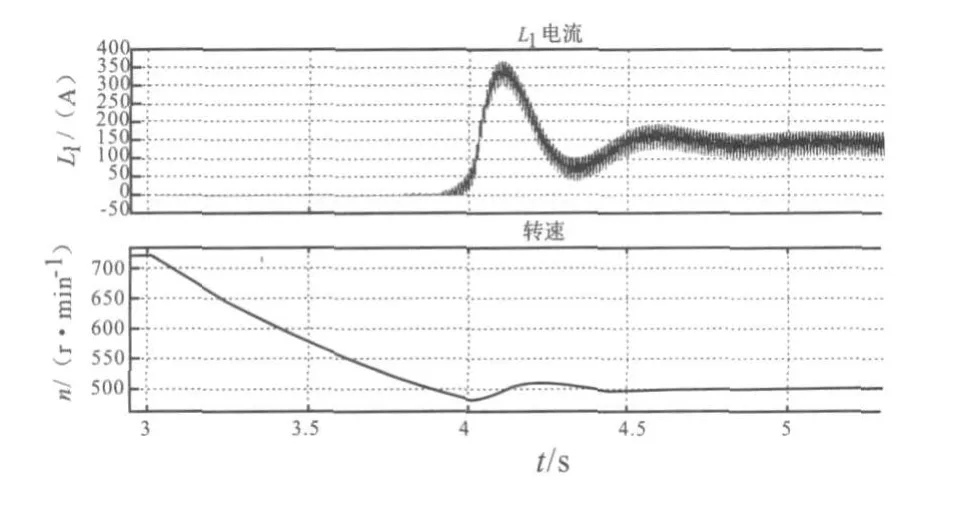
图5 720 r/m in调整到给定转速 500 r/m in电流、转速动态过程波形Fig.5 Dynam ic process of the current wave and speed when speed at 720 r/m in ad justs to the given speed 500 r/m in

对系统在 500 r/m in稳定后突加负载 2 000 N◦m,仿真结果如图 6。可以看出系统动态最大速降为 5 r/min,在 2%误差带内,抗扰效果良好,双闭环结构较好地控制了直流母线电流的波动。

图5和图 6中流过 L1的电流都含有大量的高次谐波分量,这主要是由于对于任何一种串级调速系统,流过转子绕组的电流都不再是正弦波,而是矩形波或有换流交叉角的梯形波,这就是电流的高次谐波分量。

图6 5.2 s突加 2 000N◦m负载扰动后电流、转速动态过程波形Fig.6 Dynam ic processw aveform of current and speed after applied a load of 2000 N◦m at 5.2 s

4 结 论

通过对斩波式串级调速双闭环控制系统的仿真实验可以看出,本文所设计的双闭环控制调节器,能够很好地控制系统由于负载波动引起的直流母线电流的波动、转速波动,使系统能够较快跟随转速设定,能够满足实际应用的要求。

[1]许畅.高频斩波串级调速系统的建模与转速控制研究[D].保定：华北电力大学,2006.

[2]江友华.高压大功率异步电动机驱动风机—泵类负载调速技术的研究 [D].上海：上海大学,2006.

[3]孙金水.斩波内馈串级调速系统的基础研究 [D].保定：华北电力大学,2007.

[4]陈伯时,陈敏逊.交流调速系统 [M].北京：机械工业出版社.1998.

[5]谢胜利.串级调速系统谐波与功率因数的仿真研究[D].保定：华北电力大学,2007.

[6]崔健.斩波式串级调速系统的研究与改进 [D].保定：华北电力大学,2002.

[7]马永光,张晓东,王兵树,等.串级调速电机的动态模型与仿真 [J].电机与控制应用.2007,34(1)：11-14.

[8]于希宁,刘红军.自动控制原理 [M].北京：中国电力出版社.2001.

[9]张锡憬,陶维青.串级调速双闭环系统动态响应的计算机分析及综合 [J].安徽工学院学报.1986,5(1)：101-116.

[10]王君艳.交流调速 [M].北京：高等教育出版社,2003.

[11]徐书确.双闭环串级调速系统的静态计算和动态设计 [J].电气传动.1984,(4)：9-16.

Research and Simulation of Internal Feedback Cascade Speed-control System

Liu Yan1,Wang Bingshu2
(1.School of Controland Computer Engineering,North China Electric PowerUniversity,Baoding 071003,China;2.Institute of Simulation and Control Technology,North China Electric Power University,Baoding 071003,China)

According to themodern double loopcascade speed-control system principle,analyzed and builtamodern cascade speed-control double closed loopcontrol system model,using MATLAB/SI MULINK tool setupmodern cascade speed-control double closed loopcontrol system simulation model.Through the simulation results verify the double closed loopcontrol strategy of the whole system can geta good performance.

cascade speed-control system;doubleclosedloopcontrol; Matlab/Simulink

TP273

A

2010-04-26。

刘岩 (1981-),男,硕士研究生,E-mail：liu_yan_081@163.com。