非饱和土粘弹性地基一维固结特性分析

秦爱芳, 罗 坤, 孙德安

(上海大学土木工程系,上海 200072)

国外研究学者从 20世纪 60年代开始研究非饱和土固结问题,典型的有 Blight[1],Scott[2], Barden[3],Fredlund[4-5]等提出的固结方程.20世纪90年代,非饱和土固结问题是国内非饱和土力学研究的热点,杨代泉[6]、陈正汉[7-9]、沈珠江[10]、殷宗泽[11]等先后研究了非饱和土的固结理论,并提出各自的见解.在非饱和土固结理论中比较完善的、具有权威性的是 Fredlund固结理论[4-5].

流变性作为土的重要工程性质之一,引起了人们的高度重视.一些学者如陈宗基[12]、门福录[13]、赵维柄[14]、李冰河[15-16]等将粘弹性模型如Maxwell, Kelvin及Merchant等模型引入到固结理论中,相应的固结理论也得到了发展.但他们的研究都是针对饱和土,前面所介绍的非饱和土固结理论又都是针对弹性地基,目前对于粘弹性非饱和土地基固结的研究还很少.

如果已有线弹性解,引入柔度系数的 Laplace变换式V(s)来代替线弹性模型中的常数 1/E,便可解决粘弹性情况的同一问题,这个思想首先是由 E. H.Lee提出,被称为李氏比拟法.钱家欢在求解固结问题时扩展了李氏比拟法的适应范围.本研究在粘弹性非饱和土固结问题求解中采用李氏比拟法.

秦爱芳等[17]首次基于 Fredlund的非饱和土一维固结理论得到一个有限厚度,且在大面积均布瞬时加载下,表面为透气透水面、底面为不渗透面的线弹性非饱和土层一维固结的解析解.此方法可向多种边界条件拓展.本研究在此基础上采用李氏比拟法研究表面排气不排水、底面不渗透的粘弹性非饱和土层的一维固结问题,得到了超孔隙水压力、超孔隙气压力及土层沉降的半解析解;给出了一个典型算例,探讨该边界下不同气、水渗透系数比 ka/kw下,Kelvin体中弹性模量 E1和粘滞系数η等对非饱和土粘弹性地基的固结规律的影响,得到相关的固结曲线,揭示了非饱和土粘弹性地基的固结特性;最后,通过拟弹性情况下 (非饱和土粘弹性地基的粘滞系数为零)半解析解与弹性地基解析解的对比,从而验证了半解析解的正确性.

1 计算简图和本构模型

非饱和土层如图 1所示,土层厚度为 H,地表作用有大面积均布瞬时荷载 q,坐标原点设在地表,深度方向 z向下为正,取底面积为 1、高度为 dz的单元体V0=1×1×dz为研究对象.

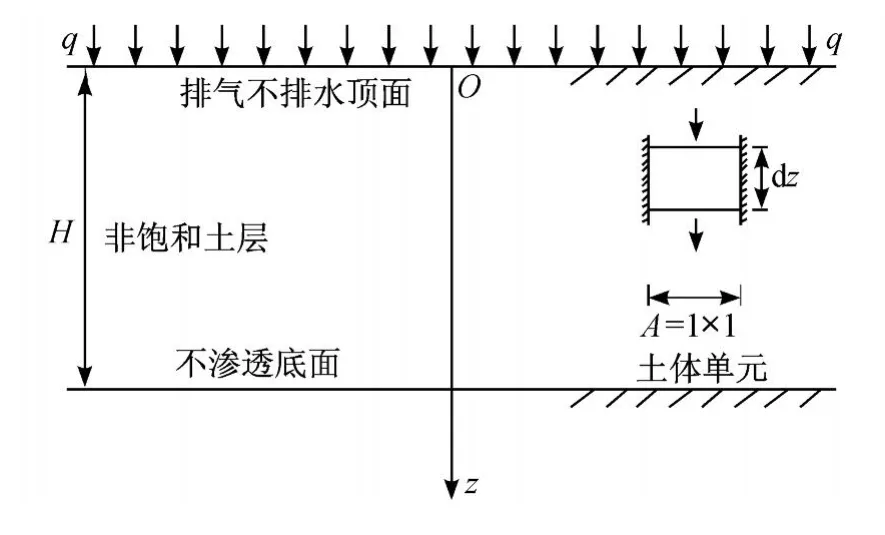
图1 非饱和土层一维固结计算模型Fig.1 S implified model for one-d imensional consolidation in unsaturated soil

本研究采用Merchant模型 (三单元模型)为粘弹性地基模型,它由一个弹性体和一个 Kelvin体串联而成,其中 Kelvin体由一个弹性体并联一个粘性体而成.模型结构如图 2所示,其本构方程为

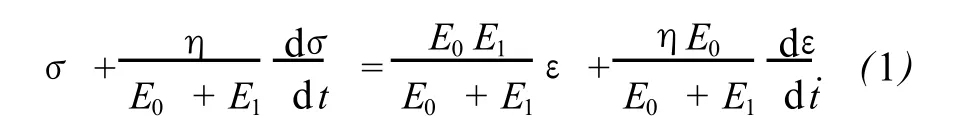
对式(1)作关于时间 t的Laplace变换,得

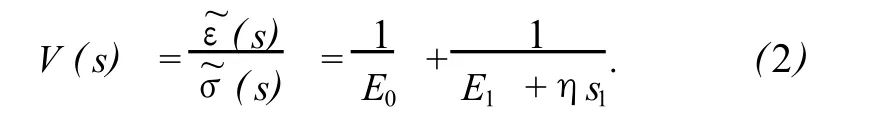
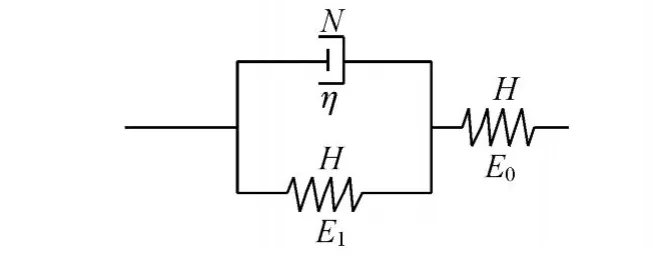
图2 M erchant模型Fig.2 M erchantmodel

2 半解析解推导

本研究基于 Fredlund的非饱和土的一维固结理论进行假设[17],针对Merchant粘弹性地基模型,应用李氏比拟法,由得到的液相及气相的控制方程、Darcy定律及 Fick定律,采用文献[17]的方法,得到Laplace变换下 4个微分方程：

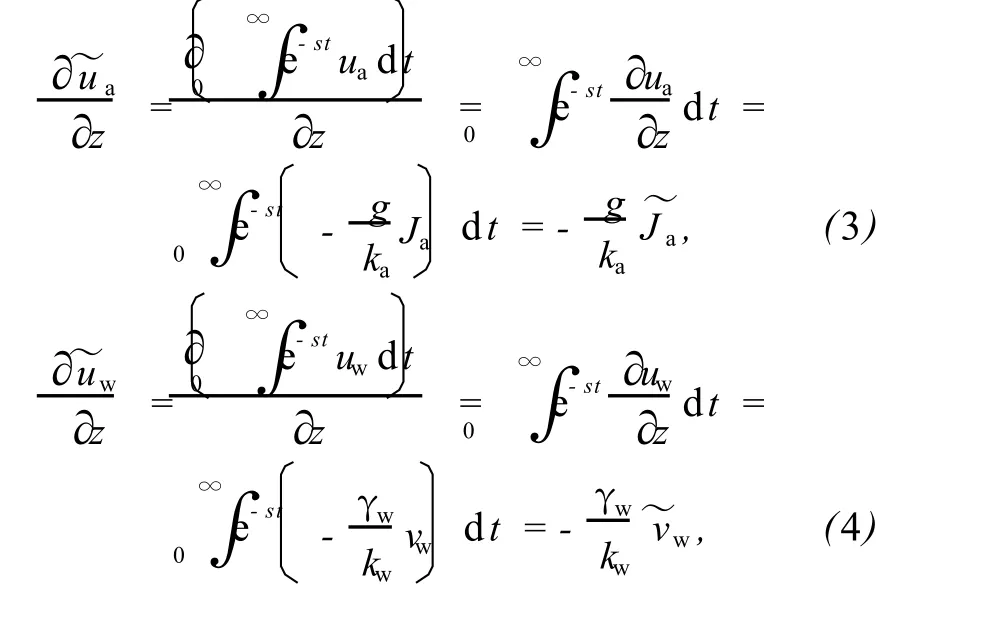
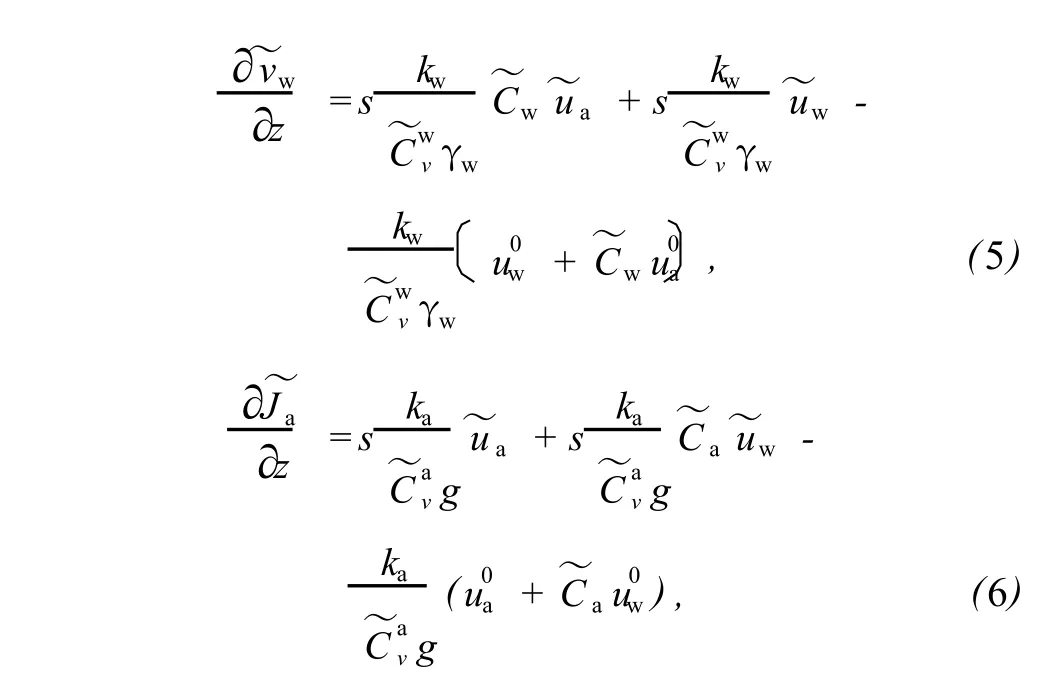
式中,

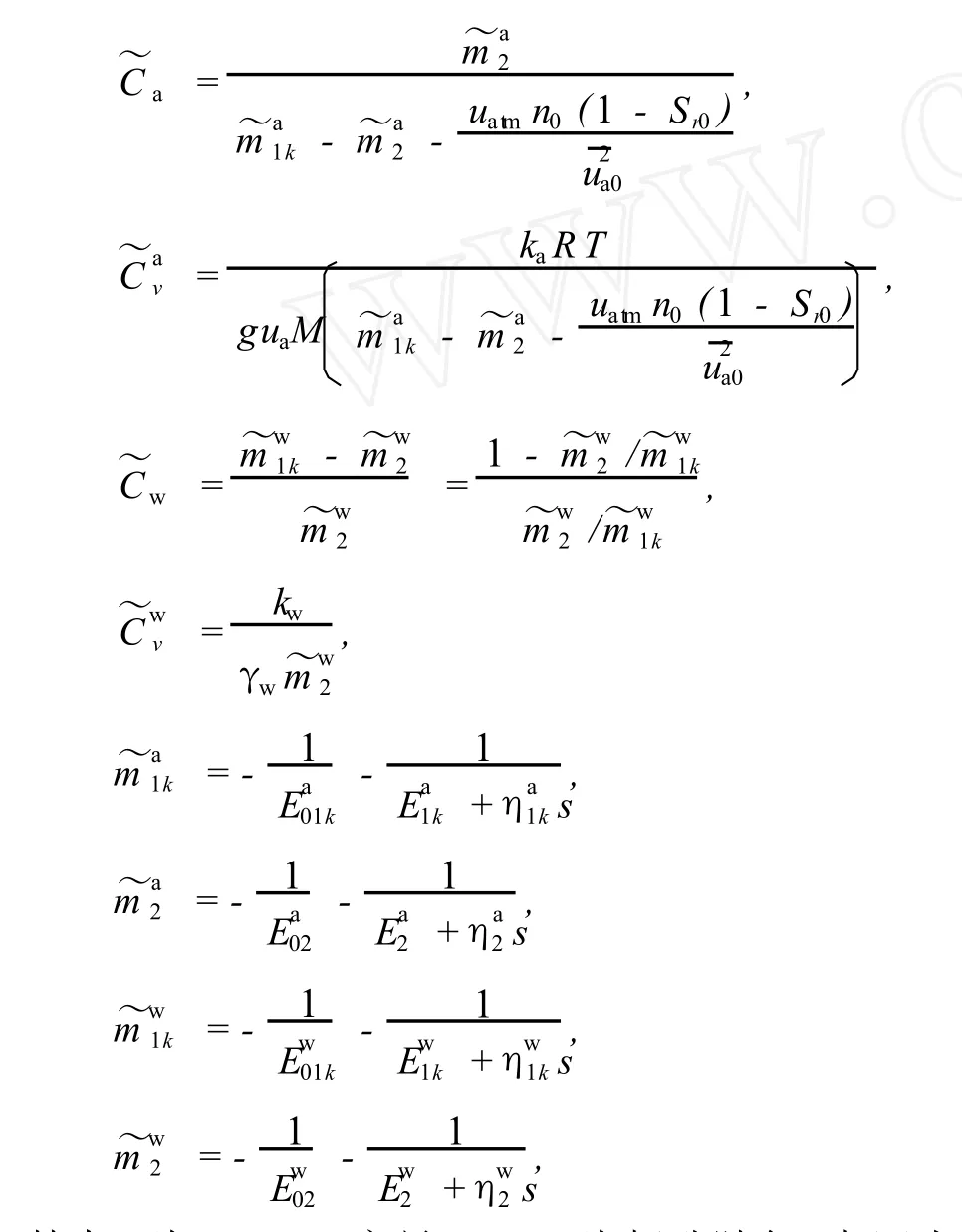
其中 s为 Laplace变量;ua,uw为超孔隙气、水压力;,为初始超孔隙气、水压力;,为超孔隙气、水压力的Laplace变换;Ja为 z方向上单位面积土体内气体的质量流动速率及其 Laplace变换; vw,为非饱和土中的水在 z方向的流速及其Laplace变换;ka为非饱和土中的气体渗透系数(m/s),假定为常数;g为重力加速度;kw为非饱和土中的液体渗透系数 (m/s),假定为常数;γw为液相的重度;Va为气体的体积;R=8.314 J/(mol·K)为通用气体常数;M为气体的平均摩尔质量;T为绝对温度;n0为负载前的初始孔隙率;Sr0为负载前的初始饱和度;,为 K加荷条件下相应于净法0向应力变化 d(σ-ua)的水体积、气体体积变化系数的Laplace变换;,为 K0加荷条件下相应于基质吸力变化 d(ua-uw)的水体积、气体体积变化系数的Laplace变换;E为相应的弹性模量;η为相应的粘滞系数.

由式(3)～(6)得到矩阵形式的常微分方程为

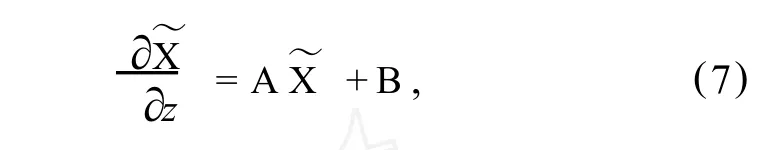
式中,

矩阵常微分方程(7)的一般解为

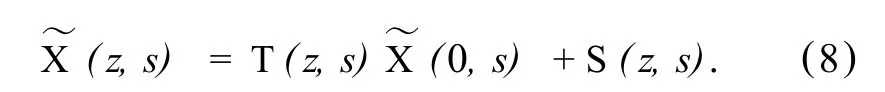
根据 Cayley-Hamilton理论[18],可求得矩阵 T (z,s),S(s).

土层顶面为排气不排水面,底面为不渗透面,所以边界条件为

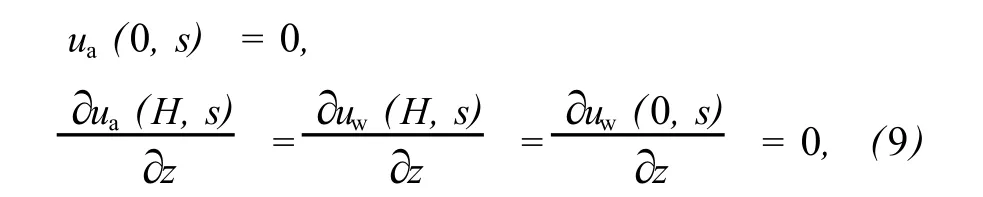
初始条件为

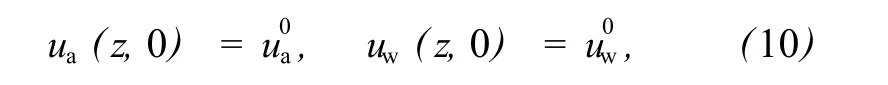
可解得Laplace变换下任意深度处的超孔隙气压力和超孔隙水压力为

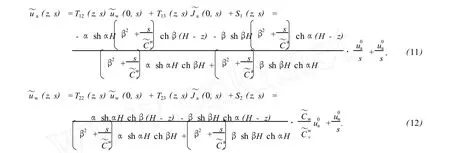
进一步可求得

对于简单的 Laplace逆变换问题,可直接利用Laplace逆变换的数学表达式解决.而对于本研究,(z,s),(z,s)及(z,s)都极其复杂,且无法用解析式表示,需通过数值法进行逆变换.本研究采用精确度较高、较常用的Drubin和 Crump[19]方法编制程序对式(11)～(13)进行 Laplace逆变换,得到时间域内土层内任意深度、任意时间的超孔隙气压力、超孔隙水压力及任意时刻地表沉降量.

3 计算与分析

设一水平方向无限的土层,层表面排气不排水,层底不排气不排水,主要土层参数如下：

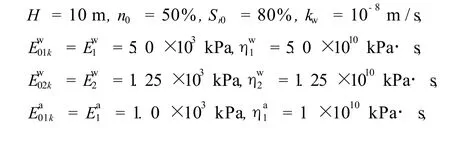
图3～图 5表现了不同 ka/kw条件下超孔隙气压力、超孔隙水压力及土层沉降随时间的变化规律.从图 3可以看出：超孔隙气压力的消散是在相对较短的时间内完成的;ka/kw越大,超孔隙气压力越早开始消散;在对数坐标下,各种 ka/kw情况下,超孔隙气压力消散曲线的切线斜率 (消散率)几乎相同.从图 4可以看出：ka/kw越大,超孔隙水压力越早开始消散,与超孔隙气压力的消散规律类似;当超孔隙气压力消散结束后,由于不排水,超孔隙水压力将停止消散.从图 5可以看出：当 ka＜kw时,土层沉降随时间变化曲线呈反 S形,类似于饱和粘弹性土固结沉降曲线;当 ka≥kw时,土层沉降随时间变化曲线呈双 S形.从图 5中还可以看出,前期 ka/kw越大,土层沉降开始越早,且当 ka≥kw时,中间有一段相对平缓的阶段;后期不论 ka/kw值是多少,沉降曲线均趋于一致.这是由于后期超孔隙气压力消散完成后,不排水导致超孔隙水压力也不消散.此外,当超孔隙气压力、超孔隙水压力均完成消散后,粘弹性地基土层并没有完成固结,还有较大的沉降量发生,这是由于土的粘滞性造成的.

图3 不同 ka/kw条件下土中超孔隙气压力 ua/q随时间的变化规律Fig.3 Change in excess pore gas pressureua/qin soil with t ime under differentka/kw

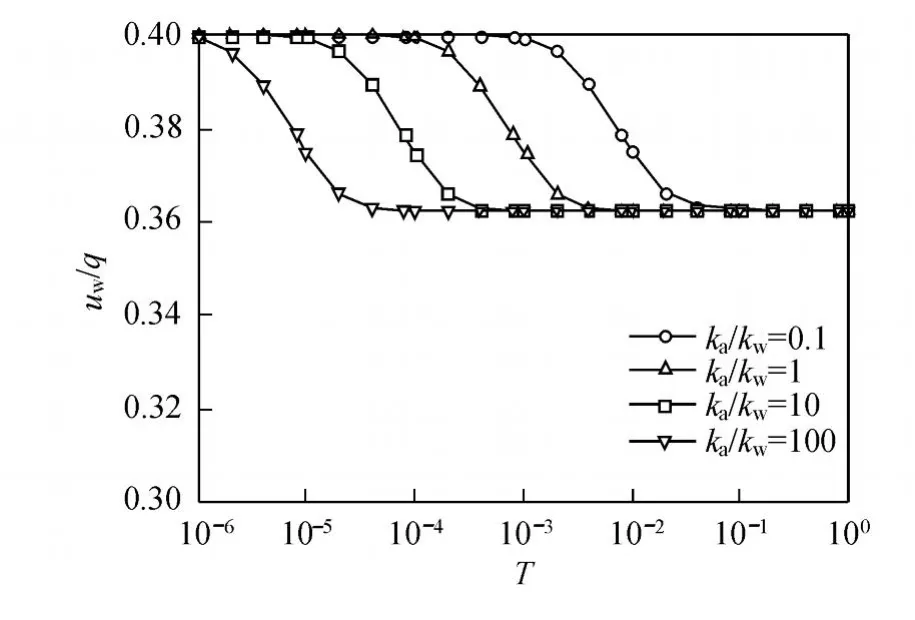
图4 不同 ka/kw条件下土中超孔隙水压力 uw/q随时间的变化规律Fig.4 Change in excess pore water pressureuw/qin soil with t ime under differentka/kw

图6为不同粘滞系数η下,土层沉降随时间变化规律.可以看出：在拟弹性情况下,土的固结速度比其他情况都要快,且固结曲线呈反 S形;当粘滞系数η较大时,固结曲线呈双 S形.前期(超孔隙气压力消散结束前)固结曲线趋于一致,且均比拟弹性情况下固结沉降稍小;后期 (超孔隙气压力消散结束后),粘滞系数越大,土的固结越缓慢,并且完成固结所需要的时间越长,这说明粘滞系数对土的固结的影响主要体现在固结过程的后期.

图5 不同 ka/kw下沉降随时间的变化规律Fig.5 Change in soil layer settlement with t ime under differentka/kw

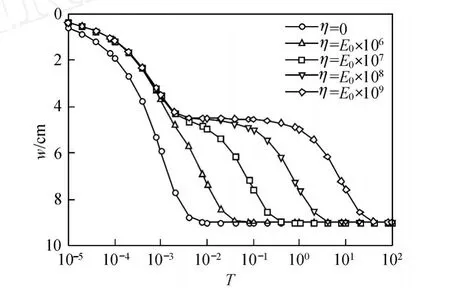
图6 ka/kw=1时不同粘滞系数η下沉降随时间的变化规律Fig.6 Change in soil layer settlement with t ime under different coefficient of viscosityηwhenka/kw=1

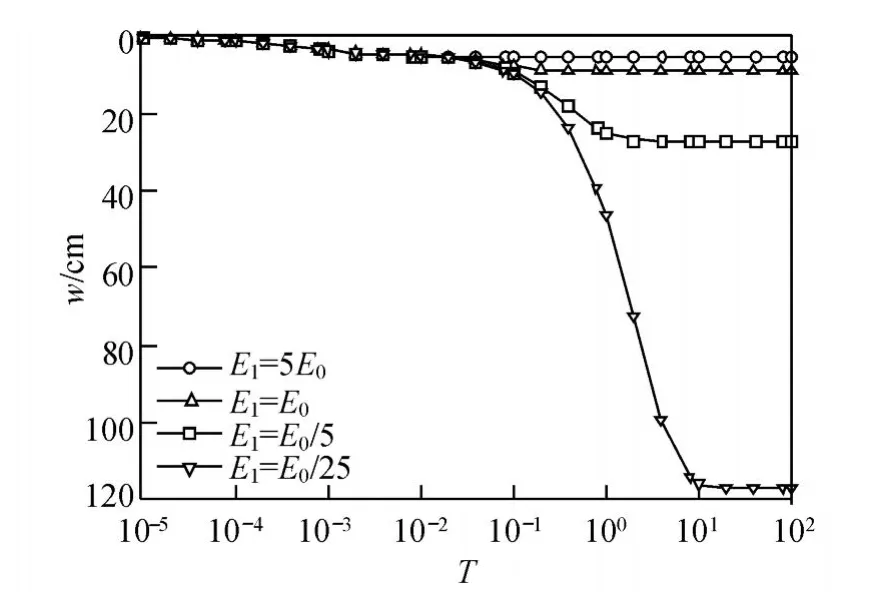
图7 ka/kw=1时不同弹性模量 E1下沉降随时间的变化规律Fig.7 Change in soil layer settlement with t ime under different elastic ratioE1whenka/kw=1

图7为不同弹性系数 E1下沉降随时间的变化规律.从图中可明显看出,随着 E1的减小,土的固结沉降增大,前期土的固结沉降量基本不变.这说明Kelvin体中弹性模量E1对土的固结的影响,也是主要体现在固结过程的后期.

图8～图 10对比了非饱和土弹性地基一维固结的解析解与拟弹性情况下的半解析解的超孔隙气压力、水压力及沉降随时间的变化规律.从图 8可以看出,两条曲线呈相同规律,且曲线趋于一致.从图9可以看出,两条曲线呈相同规律,但弹性情况下,最终超孔隙水压力消散比拟弹性情况快一些.从图10可以看出,弹性情况与拟弹性情况固结曲线趋于一致,这也说明半解析方法是正确的.

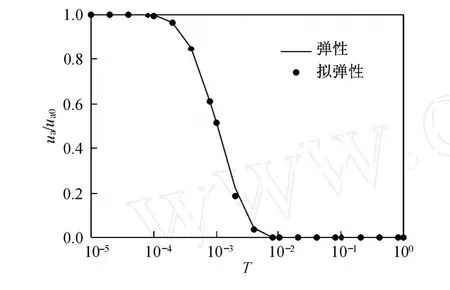
图8 弹性和拟弹性情况下土中超孔隙气压力 ua/ua0随时间的变化规律Fig.8 Change in excess pore gas pressureua/ua0in soil with t ime under the elastic situation and the elastic s imulation situation

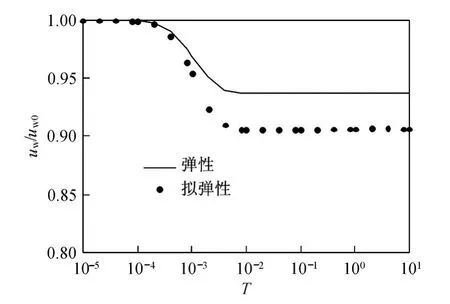
图9 弹性和拟弹性情况下土中超孔隙水压力 uw/uw0随时间的变化规律Fig.9 Change in excess pore water pressureuw/uw0in soil with t ime under the elastic situation and the elastic s imulation situation

4 结 论

本研究采用李氏比拟法,针对Merchant粘弹性地基模型,采用Laplace变换等数学方法,建立求解非饱和土粘弹性地基的一维固结的半解析方法,所解的问题考虑有限厚度的粘弹性非饱和土层,处于一维受荷状态,土层表面为排气不排水面,底面为不渗透面,取得以下结论：

(1)非饱和土粘弹性地基的固结过程中,超孔隙气压力、水压力的消散呈相同规律,ka/kw越小,超孔隙气压力、水压力越早开始消散,且均在较短时间内完成.超孔隙气压力消散完成后,由于不排水,超孔隙水压力也停止消散.

(2)当 ka＜kw(即 ka/kw=0.1)时,初期沉降较缓慢,沉降随时间变化曲线呈反 S形,类似于饱和土固结沉降曲线;而当 ka≥kw时,沉降随时间变化曲线呈双 S形.

(3)Merchant模型中,Kelvin体的弹性模量 E1和粘滞系数η对非饱和土粘弹性地基的固结规律的影响主要体现在固结过程的后期,数值越大,后期土的固结越缓慢.

(4)对比了非饱和土弹性地基一维固结的解析解与拟弹性情况下的半解析解的超孔隙气压力、水压力及沉降随时间的变化规律,它们均呈相同的规律,曲线趋于一致,证实了半解析解的正确性.

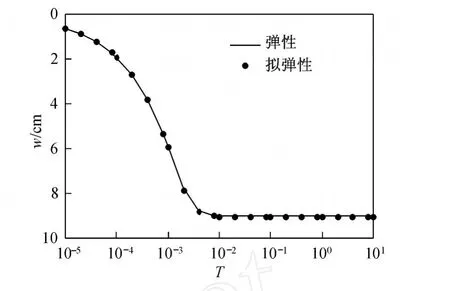
图10 弹性和拟弹性情况下沉降随时间的变化规律Fig.10 Change in soil layer settlement with t ime under the elastic situation and the elastic s imulation situation

[1] BL IGHTG E.Strength and consolidation characteristics of compacted soils [D]. England：University of London,1961.

[2] SCOTTR F.Principles of soilmechanics[M].Boston：AddisonWesley Publishing Company,1963.

[3] BARDENL.Consolidation of compacted and unsaturated clays[J].Geotechnique,1965,15(3)：267-286.

[4] FREDLUNDD G, HASAN J U. One-dimensional consolidation theory unsaturated soils[J]. Canadian Geotechnical Journal,1979,17(3)：521-531.

[5] FREDLUNDD G,RAHARDJOH. Soil mechanics for unsaturated soil[M].New York：JohnW iley and Sons, 1993：224-226;525-578.

[6] 杨代泉.非饱和土广义固结理论及其数值模拟与试验研究[D].南京：南京水科院,1990.

[7] 陈正汉.非饱和土固结的混合物理论-数学模型、试验研究、边值问题[D].西安：陕西机械学院,1991.

[8] CHENZ H,XIED Y,L IUZD.Consolidation theory of unsaturated soil based on the theory of mixture(Ⅰ) [J].Applied Mathematics and Mechanics：English Edition,1993,14(2)：137-150.

[9] CHENZ H. Consolidation theory of unsaturated soil based on the theory of mixture(Ⅱ) [J].Applied Mathematics andMechanics：English Edition,1993,14 (8)：721-733.

[10] 沈珠江.非饱和土简化固结理论及其应用 [J].水利水运工程学报,2003(4)：1-6.

[11] 殷宗泽.土工原理[M].北京：中国水利水电出版社, 2007：350-364.

[12] 陈宗基.固结及次时间效应的单向问题[J].土木工程学报,1958,5(1)：1-10.

[13] 门福录.粘土固结与次时间效应单维问题的近似解[J].水利学报,1963(1)：44-63.

[14] 赵维柄.广义Voigt模型模拟的饱水土体一维固结理论及其应用[J].岩土工程学报,1989,11(5)：78-85.

[15] 李冰河,谢康和,应宏伟,等.变荷载下软粘土非线性一维固结半解析解[J].岩土工程学报,1999,21(3)：288-293.

[16] 李冰河,谢康和,应宏伟,等.初始有效应力沿深度变化的非线性一维固结半解析解 [J].土木工程学报, 1999,32(6)：47-52.

[17] Q INA F,CHENG J,TANY W,et al.Analytical solution to one dimensional consolidation in unsaturated soils[J].AppliedMathematics andMechanics：English Edition,2008,29(10)：1329-1340.

[18] KORNGA,KORNT M.Mathematical handbook for scientists and engineerings[M].New York：McGraw-Hill Inc,1968.

[19] DURB INF. Numerical inversion of the Laplace transfor ms：an efficient improvement to Dubner and Abate’smethod[J].Comput J,1974,17：371-376.