卫星和飞船跟踪测控的数学模型

张海基，蔡逢演，叶惠城，陈燕燕

(广州科技贸易职业学院 基础部，广东 广州 511442）

1 问题分析

本文讨论的问题是2009年“高教社”杯全国大学生数学建模比赛C题.

卫星按运行状况可分为同步卫星与非同步卫星，而同步卫星又分为同步静止卫星、倾斜轨道卫星和极地轨道同步卫星.对于问题一，要让测控站所在平面与卫星轨道共面，且卫星只能在赤道上空运行，只有同步轨道静止卫星符合条件.如果该卫星为非同步卫星，那该卫星距离地球表面的高度处于一个范围值，即在围绕地球运行的最小高度与最大高度之间.

对于问题二，在地球自转的影响下，卫星运行过程中星下点轨迹在地球表面形成一些“8”字型的轨迹，对称地分布在赤道两边.考虑到卫星星下点轨迹的密集程度问题，对于星下点轨迹圈数较少的卫星，可根据其相应的轨迹进行分析求解；由于测控站在卫星轨道面的测控区域是个圆形，因此对于星下点轨迹圈数较多较密的卫星，利用测控区域的圆内接正方形来覆盖整个卫星轨道面，从而计算出全程监控所需的最少的测控站的个数.

在不影响求解的前提下，为了简化问题，提出以下模型假设：(1) 卫星的运行轨道为圆形；(2) 地球是一个球体；(3) 不考虑对卫星或飞船的发射和降落的监控；(4) 忽略外界对研究对象的影响(如其他天体对卫星的万有引力等)；(5) 卫星运行方向和地球自转方向相同；(6) 卫星的运行角速度 地球自转角速度.

2 模型建立和求解

2.1 问题一的求解

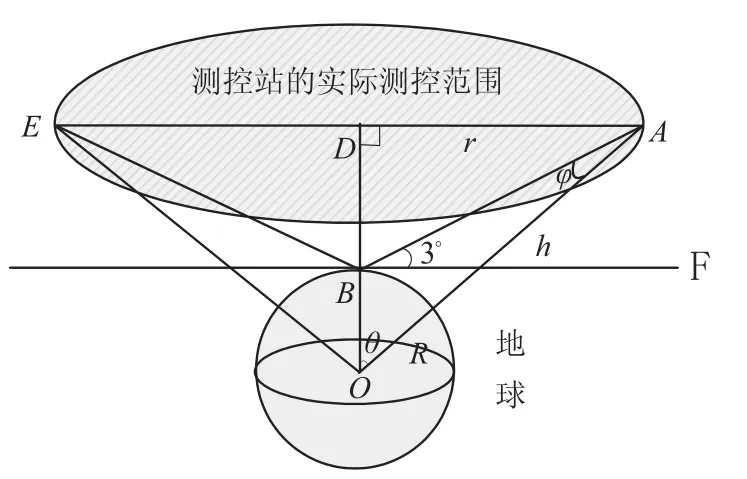
图1

由于测控设备只能观测到所在点切平面以上的区域，且在与地平面夹角3°的范围内测控效果不好，因此，除去与地平面夹角3°内的范围，考虑实际测控范围与卫星轨道面的相交圆，利用每个相交圆的直径在地心所对的圆心角2θ(即∠AOE，如图1所示)，即可计算出全程监控所需的最少的测控站个数.

如图1所示，点O为地心，圆D为测控站实际测控范围与卫星轨道面的相交圆，地球半径为R，圆D的半径为r，卫星距离地面的距离为h，切线BF落在平面AOE上，B为切点.因此，在平面AOE上，r=(R+h)sinθ，∠ABF=3°，测控角度∠ABE=174°.在ΔOAB中，有∠ABO=93°，由正弦定理得由三角形内角和定理得所以测控站个数

从上述模型看出，测控站的个数与卫星距离地面的高度有关.在一定条件下，随着卫星距离地面高度的增大，测控站的个数会随之减少.

由于人造卫星离地面的最低高度介于100～110 km之间，所以将卫星距离地球表面的最低高度为100 km代入表达式可求出测控站个数为24个；当卫星距离地面高度越来越大时，卫星测控站个数越来越少.设卫星在离地球一定远处刚好脱离地球引力向外运行，此时卫星的高度趋向无穷大，由测控站个数的表达式可得至少需要3个测控站才可以全程监控卫星；当卫星达到同步轨道静止卫星的高度时，其运动周期与地球自转周期一样，卫星与地球相对静止，此时只需要1个测控站就可以进行全程跟踪测控.

2.2 问题二的求解

由于一个卫星或飞船的运行轨道与地球赤道平面有固定的夹角，而且地球自转时该卫星或飞船在运行过程中相继两圈的经度有一些差异，因此，对卫星在地球表面的星下点轨迹进行分析.

(1) 当卫星运行角速度与地球自转角速度相同时，卫星沿运行轨道运行一圈后星下点轨迹又回到起点.星下点轨迹见图2(相继两圈的经度无变化，不合题意).

(2) 当卫星运行角速度是地球自转角速度的两倍时，卫星沿运行轨道运行两圈后星下点轨迹回到起点.星下点轨迹见图3.

(3) 当卫星运行角速度是地球自转角速度的三倍时，卫星沿运行轨道运行三圈星下点轨迹回到起点.星下点轨迹见图4.

图2

图3

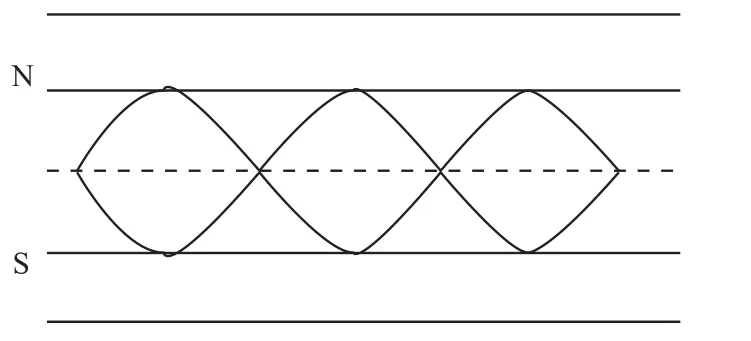
图4

(4) 卫星运行角速度越大，卫星在地球表面上留下的星下点轨迹越密，从而形成了如图5所示的星下点轨迹.

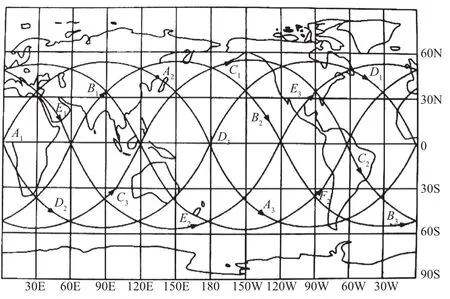
图5 卫星星座的地面轨迹

由以上图形观察和分析可以得出：星下点轨迹均匀地分布在赤道的两边，即南纬α与北纬α之间.因此，在卫星或飞船的星下点轨迹较为简单的情况下可沿着星下点轨迹设立测控站(如上述(2)、(3)的情形)；对于一般情况，特别是卫星或飞船的星下点轨迹较密时(如情形(5))，只需测控南纬α与北纬α之间的区域，就可以实现对该卫星的全程测控.

在实际测控范围与卫星轨道面的相交圆D中取圆内接正方形(如图4)，并用内接正方形覆盖所要测控的区域(如图4、图5).首先根据轨道面与赤道面的夹角α以及每个内接正方形边长在地心所对的圆心角2β，可求出测控区域中正方形的行数j，如图6所示；其次，根据每一行正方形覆盖的轨道面的圆周长即可确定每一行所需的正方形的个数i，从而计算出全程监控所需的测控站的最少个数如图7所示.求解过程如下：

(1) 计算正方形的边长在地心所对的圆心角为2β.如图8，过D作DC⊥AC，则有如图9，连接OD(点O为地心，D为实际测控范围与卫星轨道面的相交圆的圆心)和OC(点C为正方形边长的中点)，则在RtΔODC中有所以又因为r=(R+h)sinθ，OD=(R+h)cosθ.则可求出

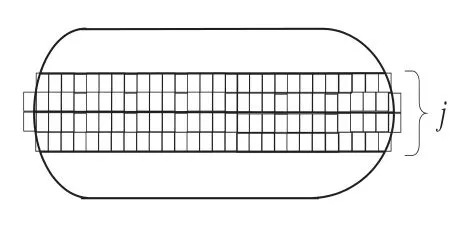
图6

图7

图8

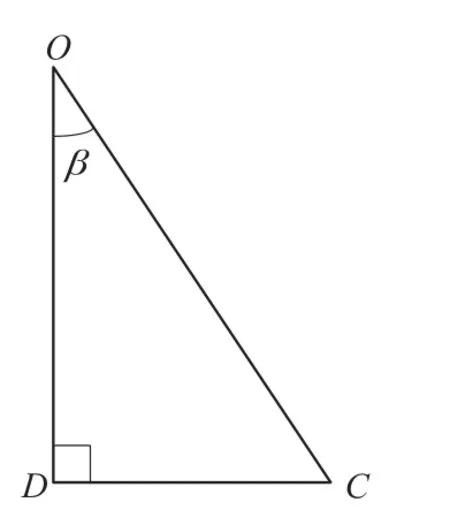
图9

由于卫星围绕地球运动时，轨道与赤道平面有一个夹角α，测控范围由正方形覆盖，所以正方形的行数j为

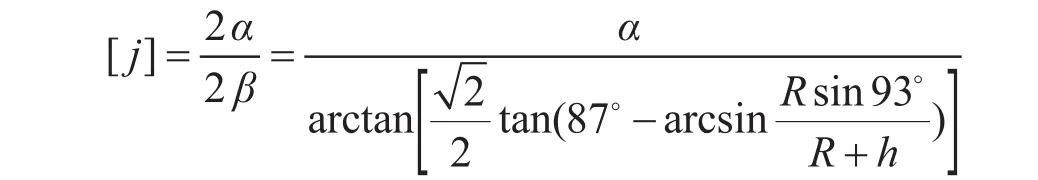
圆内接正方形每条边在卫星轨道面上所对的圆弧长为

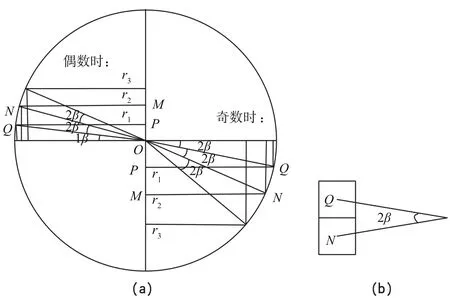
图10

(2) 当[j]为偶数时，各行正方形在南北纬之间对称分布(如图7所示)，结合图7与图10，每一行正方形的总长度是正方形所在轨道面的圆周长，北纬第一行正方形覆盖的轨道面圆周长C1=2π(R+r)cosβ，因此，北纬第一行排列的正方形个数北纬第二行正方形覆盖的轨道面圆周长为C2=2π(R+r)cos3β，因此，北纬第二行排列的正方形个数依此类推，北纬第x行上分布的测控站的个数[nx]=为实现全程测控的测控站总个数为当[j]为奇数时，先用一行正方形覆盖赤道(正方形中心在赤道上)，然后将各行正方形在南北纬之间对称分布.显然，赤道上排列的正方形的个数为.南纬第一行正方形覆盖的轨道面圆周长为C1=2π(R+r)cos2β，因此，南纬第一行排列的正方形个数依此类推，南纬第x行正方形覆盖的圆周长Cx=2π(R+r)cos2βx，因此，南纬第x行上分布的测控站的个数为最终，实现全程测控的测控站总个数为[n] =2

为了验证上述模型，现将神舟七号的数据(神舟七号的轨道与赤道平面夹角为42.2°，神舟七号距离地面的高度为343 km)代入[j]的表达式可得[j]=4，所以要用偶数行的模型进行求解总的测控站数n=2n1+2n2=60，因此，神舟七号只要60个测控站就可以实现全程测控.

3 模型改进推广

问题二中，为使计算方便，采用内接正方形覆盖所要测控的区域.圆内接正方形的面积占圆面积的63.69%，而圆内接正六边形的面积占圆面积的82.74%，因此可以考虑采用圆内接正六边形覆盖，以提高有效覆盖率.另外，在某些具体问题上，采用内接正方形或内接正六边形覆盖所要测控的区域，会出现较多的浪费，这时不能一味追求圆内接图形面积占圆面积的比率，而应该从整体的角度来考虑测控站的最优分布.

[1] 赵亚辉.测控站应该怎么分布才能覆盖地球[EB/OL].(2009-09-11)[2009-10-02].http：//wenda.tianya.cn/wenda/thread?tid=1 1ff695a383272df.

[2] 于泽远.中国航天史首次神七今天执行出舱任务[EB/OL].(2008-09-27)[2009-09-11].http：//www.zaobao.com/special/china/ shenzhou/pages1/shenzhou7080927.shtml.

[3] 姜启源.数学建模[M].北京：高等教育出版社，2006.