偏压状态下新建隧道下穿既有构筑物合理施工方法研究

汪 波,张 胜,何 川

(1.西南交通大学地下工程系,成都 610031；2.安徽省交通规划设计研究院,合肥 230031)

1 概述

随着土地利用的日益紧张和交通设施需求的不断增加,在城市繁华地区或一些特定地段,有时需要在既有隧道旁新建隧道或者一次性修建多孔近距离平行或交叉隧道,这种状况在国内外都不乏其例。但由于近距离交叠隧道间的相互影响使其在施工、设计上较之单孔及水平平行隧道更难于控制[1],故虽国内外对这类问题研究较多,但研究尚处于从个案上升到理论的阶段。从已有的研究来看,后施工隧道开挖将使围岩应力场在原来演变的基础上再次演变,造成既有隧道的安全性以及相互影响带来的工法、工序和对策优化等问题。由于空间关系、隧道施工顺序、地质条件和施工方法等不同,影响程度也各异,需要进行与施工过程相关的分析研究[2～3]。

本文所研究叠交隧道上部为已建的人防通道,下部为新建隧道,依据设计资料可知,两隧道均处于偏压状态,其中人防隧道处于横向偏压,而新建隧道处于纵向偏压,二者均处于不利的受力状况,同时人防通道与新隧道间有效间距在7 m左右(图1),在这种情况下新建隧道的施工对既有结构物——人防隧道的近距离施工时影响将是重点关注的问题。如何把对环境的影响减少到最低限度,也是地下建筑物在近距离条件下施工的核心问题。鉴于此,采用有限元数值方法对将开建的偏压状态下新隧道在不同施工方法时对既有隧道影响的演变规律进行全真模拟,为今后的设计及施工提供重要的参考依据。

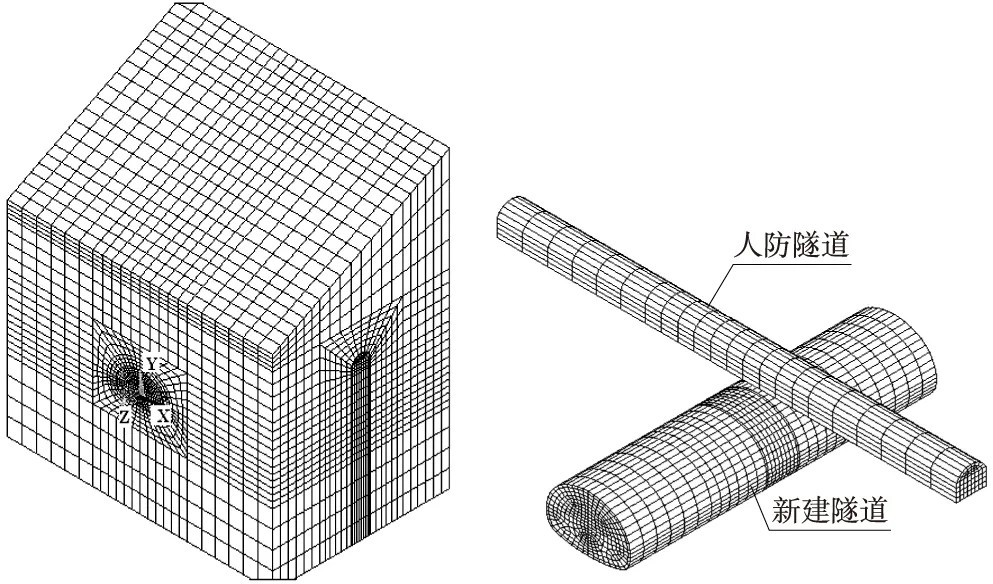
图1 有限元总体模型及空间相对位置

据前期勘查隧道区内围岩条件较好,设计中定为Ⅳ级偏高,新建隧道按分离式双洞单向行驶设计,开挖宽度约16 m,双洞轴线间距约为40 m,大于3倍的洞室半径,在此条件下,初步判断隧道开挖后应力互不叠加,故分析一个交叉口即可[4～6]。考虑到围岩条件较好及上部既有结构的重要性,施工中拟采用矿山法开挖。

2 数值模型的建立[6～8]

2.1 基本假定

在进行数值模拟过程中,做如下假定[7]。

(1)计算模型为弹塑性应变,围岩进入塑性后采用Drucker-Prager屈服准则,支护体系假定为弹性体。

(2)岩体材料是各向同性的。

(3)围岩以自重应力场为主,不考虑构造应力场的影响。

2.2 本构模型

在数值模拟过程中材料进入塑性状态后采用的D-P屈服准则表达式如下

(1)

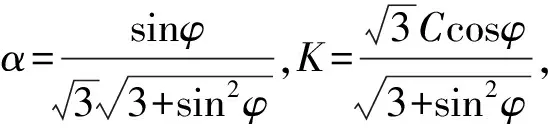
2.3 计算模型的建立

计算中模型建立依据以往的隧道力学经验,一般选取3～5倍洞径为计算区域[5～6],计算中依据实际断面形状建立计算模型,模型建立时横向取100 m、高度(即隧道的埋深)方向选取隧道仰拱底部以下约30 m、竖直向上按照实际地形坡度取至地表(地表坡度近23度,人防通道拱顶部埋深约29 m,高差约30 m),轴向取60 m。计算模型的边界条件除上部为垂直荷载边界外,其余各侧面和底面为法向约束边界。分析中岩体及二衬采用实体(solid)单元,对于超前小导管注浆、锚杆等加固措施按经验采取相应的提高该区域的围岩等级来加以考虑[9～11]。共划分近34 200个单元,36 700个节点。计算模型如图1所示,物理力学参数如表1所示。

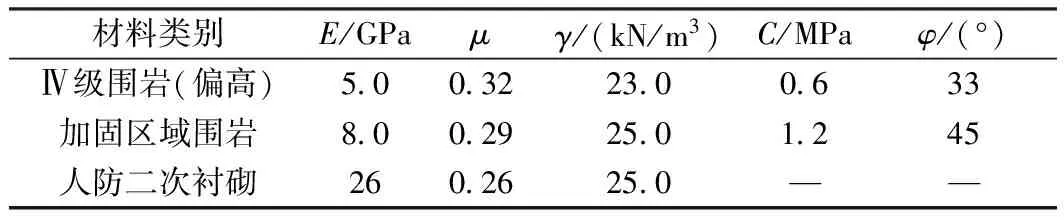
表1 物理力学计算参数的选取

2.4 施工步骤

新建隧道开挖拟采用全断面法及上下台阶法两种方案,重点研究既有人防隧道在两种不同的工法下其围岩及衬砌的演变规律并加以对比分析,以期获得最佳的开挖方式并指导后续的施工。

计算中采用有限元程序提供的“生”与“死”功能进行模拟,通过分次“杀死”和“激活”单元分别模拟隧道的分步开挖及二次衬砌施工过程。计算中共分为3种工况。

工况1：新隧道全断面开挖,围岩未采取任何加固措施；

工况2：新隧道全断面开挖,围岩采取加固措施；

工况3：新隧道上下台阶法开挖,围岩采取加固措施。

因受计算机资源的限制,计算中对施工过程做了简化：对已建的人防通道,采用全断面法一次开挖成功,形成毛洞后将开挖荷载释放50%,然后施作人防二衬,再将剩余50%荷载由衬砌和围岩共同承担[4]。分析中采用全断面及上下台阶法开挖过程见图2,其中上下台阶法开挖时错开距离为1～2倍洞径。

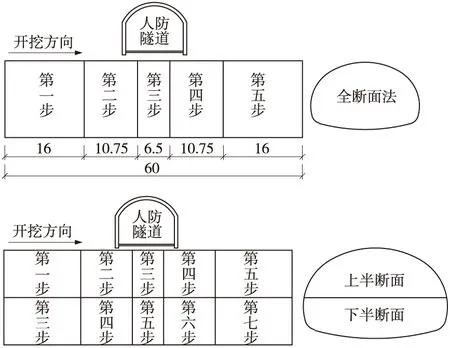
图2 开挖步骤示意(单位：m)

依据新奥法理念：应充分发挥围岩的自承载能力,故在计算过程中形成毛洞时将围岩应力释放40%再激活新建隧道的初衬[4～5]。其具体开挖步骤为：形成自重地应力场→人防隧道开挖,释放荷载50%→人防隧道支护,释放荷载50%→新隧道第一步开挖,释放荷载40%→新隧道第一步开挖处初期支护,释放荷载60%→新隧道第二步开挖,释放荷载40%→新隧道第一步开挖处初期支护,释放荷载60%→其余开挖步骤同上,整个循环全断面法共计13个施工开挖步,上下台阶法共计17个施工开挖步。

3 计算结果分析

通过上述不同工况条件下数值分析,获取了既有结构物在新建隧道不同工法下的计算结果,为清楚表达各工况条件下围岩受力及位移演变规律,选取其在横向及纵向典型位置作为研究分析路径(图3)。

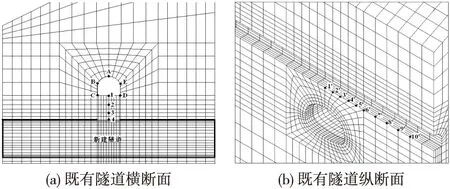
图3 研究分析路径图示

3.1 工况1条件下围岩受力及位移分析

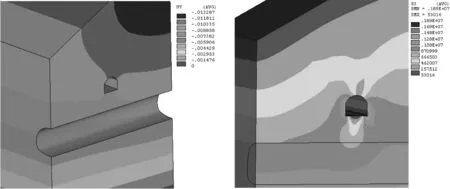
图4 人防隧道建成时围岩σ1及UY云图(含初始位移及应力)

通过数值分析获取了工况1条件下最初人防隧道建成时的围岩应力及位移云图(图4),应力以压为正,Pa；位移向上为正,m。以及随开挖步增加既有隧道围岩特征点的位移及受力变化情况(图5)。

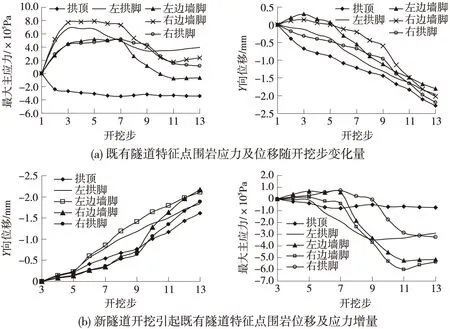
图5 既有隧道特征点围岩位移及应力变化曲线

从图4、图5中可以看出，人防隧道围岩特征点应力及位移因受横向地形偏压及新隧道建设过程中施工偏压的影响而呈现出不对称分布的特点,现分析如下。

(1)围岩受力特征：人防隧道建成之初(开挖步3),围岩总体处于受压状态,与初始应力场比较而言，除拱顶压应力减小外,其余部位压应力均将增大,最大值位于右边墙脚位置处,达0.8 MPa；人防右侧边墙的受力明显大于左侧边墙,拱脚以上拱圈部位的受力则是左侧大于右侧,究其原因是由于隧道受横向偏压作用而导致对左侧拱部产生相对较大挤压所致。随着新隧道的开挖,人防通道围岩特征点的受力状况逐渐发生变化,从图5(a)可知,相对人防通道建成之初的围岩受力情况而言,新隧道建设对拱顶受力影响较小,几乎未发生太大变化；但其他特征点的受力均将降低,降幅最大的位于左、右边墙脚处,超过0.5 MPa。具体如下：新隧道第一步开挖(开挖步5)因距离人防隧道较远,对其上述特征点的受力影响较小,几乎未发生变化；第二步开挖(开挖步7)时因受施工偏压及地形偏压的共同影响,将明显引起左拱脚的应力降低,此时,左、右侧拱脚的受力几乎相等,但边墙部位受力仍不对称,相比较人防隧道建成之初而言,不对称状况有所缓解；当开挖通过人防隧道时(开挖步9),左、右边墙脚的应力急剧降低,降幅在0.4 MPa左右,同时左拱脚的应力进一步下降,但右拱脚的受力状况变化不大,此时,由于施工已通过既有结构物,施工偏压的影响逐渐减小,围岩特征点又呈现出偏压的特性；新隧道进一步开挖(开挖步11),左、右边墙脚的应力再次降低,对右边墙脚的影响最大,其降幅达0.6 MPa左右,右拱脚的应力也显著降低,降幅在0.3 MPa左右,但此时对左拱脚受力影响较小,几乎未发生太大变化；当隧道贯通时,可以看出围岩特征点的受力状况几乎趋于稳定,均未发生太大变化,只是右边墙脚的受力稍有增加,但增幅不大,既有隧道的特征点受力最大位置由最初的右边墙脚转变为现今左拱脚处,右边墙脚与右拱脚之间的应力差减小,但左边墙脚与左拱脚之间的应力差逐渐加大。

(2)围岩位移特征：人防隧道建成之初围岩底板将产生少量隆起,其余特征点将产生下沉,最大下沉位置位于拱顶,量值达0.67 mm。相对人防建成之初围岩位移状况而言,新隧道开挖均将引起所有特征点下沉,但受施工及地形偏压的影响,下沉量有所不同,具体分析如下：新隧道第一步开挖(开挖步5)引起特征点的位移较小,不足1 mm,此时受施工及地形偏压共同影响,左、右拱脚及边墙脚处的位移几乎相当；同应力的影响相似,第二步开挖时因受施工偏压影响,将明显引起人防隧道围岩左侧部位特征点的下沉,最大沉量差位于左边墙角及左拱脚处,约1.2 mm,右侧围岩稍有沉降,但沉降量不大(图5(b))。当开挖通过人防隧道时,沉降量最大的仍位于左边墙角及左拱脚处,但右侧围岩特征点位移也明显增大,左、右边墙脚及拱脚位置的位移差达到最大,隧道处于相对不利的受力状态；随着开挖的进一步深入,新隧道将穿过既有建筑物,此时最大影响位置位于右侧边墙及拱脚处,沉降差达1.5 mm左右,其余特征点也有相对沉降,但沉降量相对较小,受施工偏压影响,左、右拱脚及边墙脚处的位移又几乎相当；当隧道贯通时,既有隧道围岩特征点进一步下沉,但沉降量有所降低,相对最大沉降量仍位于右侧围岩,受地形偏压影响,最终相对最大沉降量位于右边墙脚处,达2.2 mm,既有隧道的围岩特征点下沉规律无太大变化。

3.2 工况2条件下围岩受力及位移分析

为讨论围岩加固效果,对全断面法开挖时围岩加固条件下的人防通道特征点的应力及位移随开挖步演变规律进行了数值分析,结果如图6所示。

从图6中可以看出,工况2条件下围岩的位移及应力随开挖步的演变规律基本同工况1,但由于在开挖过程中采取了相应的加固措施,使得既有结构物的受力及位移状况都得到了改善,围岩自承载能力提高,提高幅度达0.2 MPa左右,围岩特征点位移减小,降幅约0.4 mm,但地形引起的偏压依然存在。从上述结果比较分析来看,因围岩本身性状较好,加固效果并不是十分明显。

3.3 工况3条件下围岩受力及位移分析

为确保施工安全,数值分析时对围岩加固条件下采用上下台阶法对新隧道进行了开挖,以探求在此工法下既有结构物围岩的演变规律是否有较大改善,通过数值分析,获取的结果如图7所示。

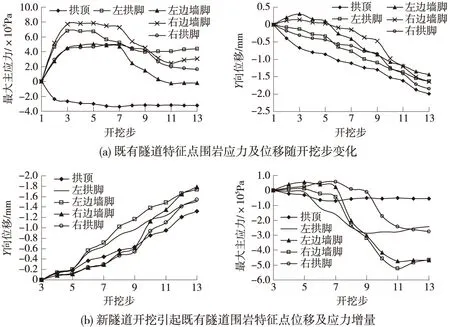
图6 既有隧道特征点围岩位移及应力变化曲线

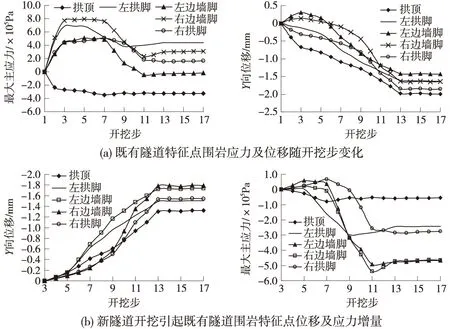
图7 既有隧道特征点围岩位移及应力变化曲线

比较3种工况下围岩的位移及应力随开挖步的演变规律可知：工况3时基本同工况1、2,其最终的结果与工况2大致相当,但由于工况3采用上下台阶法的开挖方式,使得既有结构物的受力及位移状况与同样加固围岩条件时的工况2有所不同,究其原因主要是由于上下台阶法中下台阶对围岩的应力释放和位移起了一定的抑制作用,致使每个循环开挖步之间产生的围岩应力和位移差值减小,位移减小值一般在0.4 mm左右,应力值减小虽相对较小,但相比较工况2而言,工况3中各开挖步之间的应力差值相差甚小,应力变化均匀,围岩在开挖过程中自承载能力提高,有助于既有隧道的稳定,同时从图7中还可以看出,在开挖步11——即图2中的第四步时,围岩的受力基本趋于稳定,在开挖步13——即图2中的第五步时,围岩的位移亦基本趋于稳定,后续的开挖对既有结构物的影响很小；既有隧道围岩的受力和位移主要发生在上台阶开挖的过程中,下台阶开挖对人防隧道的影响基本不大,但地形引起的偏压依然存在(图8),从图8可以看出,新隧道建成后,既有结构物仍处于横向偏压状况,应力及位移分布特征未发生太大改变,只是在量值上与未建新隧道之前存在差异；而新建隧道处于明显纵向偏压状态,最大压应力及位移位于偏压最大侧。

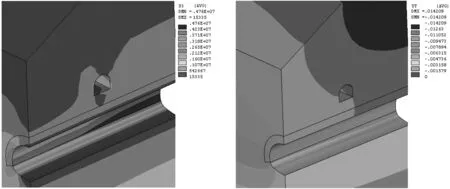
图8 新隧道贯通时围岩σ1及UY云图(含初始位移及应力)

3.4 既有隧道底板处围岩受力及位移分析

新建隧道的开挖过程中,既有隧道底板及其下部岩体内也将发生位移变化,该值也将直接反映出人防隧道结构物的稳定性,且在施工中易于实施监测,因此对其在3种工况条件下的演变规律也进行研究,具体如图9所示。

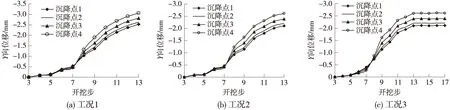
图9 新隧道开挖引起既有隧道底板围岩特征点UY增量

结合图9可以看出,随着新隧道的开挖,既有隧道底板及其下部围岩深处相对人防隧道建成之初而言也将产生位移增量,其量值随着距离新建隧道拱顶越近而越大,在工况1条件下,其最大值达3.1 mm,而工况2、3条件下最大值为2.6 mm。同时从位移变化曲线图可以看出,新建隧道全断面法开挖时第一步及最后一步的开挖对既有隧道影响较小,而中间3步开挖将是今后关注的重点,从距离来看,应在距离既有隧道前后1～1.5倍洞径位置。比较全断面法及上下台阶法可知,后者虽对围岩的最终影响与前者相同,但在开挖过程中后者能有效减小每个循环开挖步之间产生的围岩位移差值,使得既有隧道处于较为有力的受力状态,且从图9可以看出在开挖到第五步时(参考图2),围岩的深部位移亦基本趋于稳定,后续的开挖对既有结构物的影响很小,下台阶开挖影响较小。

3.5 新建隧道对既有隧道纵向影响范围的分析

新隧道在开挖过程中对既有隧道长度方向影响范围也是一个需重点研究的问题,它对于施工中既有隧道监测长度的拟定具有指导意义,基于此,本文重点对3种工况条件下新隧道贯通时引起的既有隧道沿轴向底板中心处的位移变化量来确定影响范围的大小，考虑到结构对称性,取一半特征点研究(图3),结果如图10所示。

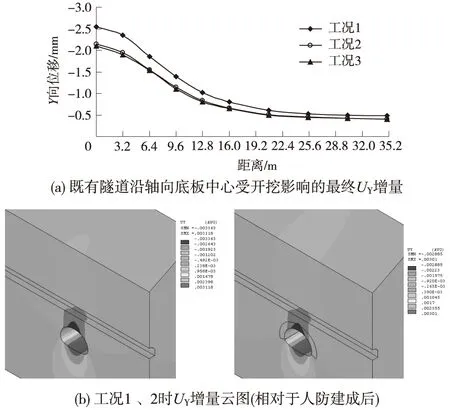
图10 新隧道开挖引起既有隧道轴向UY增量

从图10中可以看出,新隧道开挖引起既有隧道底板中心沿纵向产生了下沉,在工况1条件下,最大下沉量约达2.6 mm,而工况2、3由于围岩进行了加固,最大下沉量减小为2.1 mm左右,均位于与新建隧道中心线交汇处,距离交汇处越远,下沉量越小,距离超过20 m时,下沉量几乎保持不变,工况2、3的影响几乎相当,故位移云图只绘制了工况2时的情形。结合图10可以判断,在工况1条件下,新建隧道开挖对既有隧道产生较大影响的纵向长度范围应在新隧道中心线两侧各15 m左右,而工况2、3条件下,影响较大的纵向长度应在新隧道中心线两侧12 m左右,为保证既有隧道的绝对安全,建议取新隧道中线上既有隧道左右侧各20 m作为安全监测的范围。

综上所述,3种工况对既有隧道围岩的应力及位移的影响规律是一致的,即均将引起既有结构物特征点下沉、应力降低,只是在量值上存在差别,其中工况1影响最大,工况2、3因对围岩进行了加固,影响相对较小,但二者最终影响趋于一致,总体来看,3种工况下最终围岩的应力及位移量值较小,既有隧道将处于稳定状态。且工况3条件下各开挖步之间的位移及应力差值相差甚小,使得在开挖过程中围岩受力位移更加均匀,围岩自承载能力提高,增强了既有隧道的稳定性。从影响范围来看：横向上新建隧道在距离既有隧道前后各1～1.5倍洞径开挖时影响最大,纵向上对既有隧道影响的范围在30～40 m。

4 关于开挖方法及施工时监测项目的建议

虽通过上述3种不同工况下数值分析后认为既有隧道将处于稳定状态,但考虑到地质条件、施工方法等许多不可预见的风险因素,故建议如下[3～4]。

(1)拟建隧道一般地段可考虑采用全断面法开挖。但在两隧道交叉口处前后各2～3倍洞径范围内,为保证既有隧道的运营安全,建议采用台阶法开挖,且断面应尽快闭合,若交叉点一定范围内的岩体存在松动破碎现象,应预先进行超前加固。开挖过程中建议采用光面爆破与预裂爆破技术。断面开挖后及时采用喷混凝土及锚杆进行初支,并根据围岩变形量测结果确定二衬的合理施作时间。

(2)因两隧道交叉点处围岩厚度仅有7 m左右,故施工过程中存在一定的风险,为了保证施工的安全进行,建议在拟建隧道的掌子面推进到距离交叉点3倍洞径时,开始进行下述监测项目：

①交叉点处既有隧道的特征点、底板及其下深部围岩的下沉量测,纵向量测范围建议40 m为宜；

②交叉点处既有隧道二衬的受力量测；

③拟建隧道拱顶下沉、收敛量测；

④交叉点处新隧道围岩压力及层间支护压力量测。

根据监测结果,掌握围岩及支护的力学动态,及时反馈调整施工方法和支护参数及二衬施作时机。在掌子面超过交叉点3倍洞径跨度后,可酌情部分或全部取消上述监控项目。

5 结论

通过上述3种不同工况条件下新建隧道开挖对既有隧道影响的弹塑性数值分析可以看出,全断面法与上下台阶法均将引起既有结构物特征点下沉、应力降低,但最终围岩的应力及位移量值较小,既有隧道将处于稳定状态。同时因围岩条件较好,加固效果不甚明显,建议施工中根据具体情况采取加固措施,依据分析得出在交叉口处前后各1～1.5倍洞径范围内新隧道开挖时对既有隧道影响最大,纵向上影响范围约在30～40 m左右。同时对不同开挖条件下围岩受力及位移分析后，建议一般地段采用全断面法开挖,在两隧道交叉口处前后各2～3倍洞径范围内,建议采用台阶法开挖,并根据影响范围建议了具体的监控方案,有力地指导设计与施工。

[1]陈卫军,朱忠隆.近距离交叠隧道研究现状及评析[J].现代隧道技术,2002,39(1):42-47．

[2]仇文革.地下工程近接施工力学原理与对策研究[D].成都:西南交通大学,2003．

[3]郑余朝,仇文革.重叠隧道结构内力演变的三维弹塑性数值模拟[J].西南交通大学学报,2006,41(3):376-380.

[4]张玉军,刘谊平.上下行隧道立交处围岩稳定性的有限元计算[J].岩土力学,2002,23(4):511-515.

[5]关宝树.隧道工程设计要点集[M].北京：人民交通出版社,2003.

[6]李志业,曾艳华.地下结构设计原理及方法[M].成都：西南交通大学出版社，2003.

[7]曹云钦,王小林.浅埋偏压连拱隧道中墙优化分析[J].岩土工程学报，2006，28(4)：537-540.

[8]佘 健,何 川.软弱围岩段隧道施工过程中围岩位移的三维弹塑性数值模拟[J].岩石力学与工程学报，2006，25(3)：623-629.

[9]葛家良,陆士良.巷道锚注加固技术及其效果的研究[J].化工矿山技术,1997,26(2):13-16.

[10]张玉祥,陆士良，等.综放回采巷道支护机理及实践[J].矿山压力与顶板管理,1997(3):86-88.

[11]何 川,林 刚,汪会帮.公路双连拱隧道[M].人民交通出版社,2006.