考虑风载的接触网支持悬挂系统动力学响应分析

孙立金

(中铁道第四勘察设计院集团有限公司,武汉 430063)

1 概述

随着列车运行速度的提高,对接触网可靠性提出越来越高的要求。由于接触网/受电弓系统在工作中产生强烈振动,使接触网系统不仅受到大的静力作用,而且受到动态力的作用。作为牵引供电系统的主体接触网,其结构动态特性和在典型工况下的动力学响应,直接决定着电力机车受流质量,并最终影响列车的运行速度与安全。因此,研究其动态特性和动力学响应规律具有重要的工程实际意义。

围绕接触网的动力学分析,国内外已有不少研究工作,但同时考虑自然风载和工作载荷的研究却少见报道,因此,本文选取一个支持装置并与这个支持装置相邻的两个全档距的接触网悬挂系统作为分析对象,在叠加自然风载工况条件下,对接触网悬挂装置进行动态响应分析具有代表性。

2 接触网系统结构分析

接触网支持装置由三角形腕臂支持装置和定位装置组成,承受由承力索、接触线等组成的接触悬挂带来的悬挂荷重,并由此装置负责将接触网固定于空间一定位置,确保电力机车正常受电(图1)。

支持装置一般的外悬长度为2.3～4.0 m,视装配形式不同,其构成的三角形结构一般锐角设计值在18°～45°。所悬挂的接触网系统一般位于线路正上方,可根据受流及受力要求考虑0～±400 mm的偏置设计。

支持装置通过旋转底座与支柱等铰接连接；定位装置通过定位环与斜腕臂铰接连接；腕臂之间及腕臂斜撑通过套管双耳(或单耳)实现连接,通常此连接按固接考虑。

支持装置所承受的外力一般由支持装置、接触悬挂自身的垂直荷重；由之字力、曲线力、下锚转角力构成的水平荷重；考虑外界因素如冰、雪、风作用引起的额外荷重；以及维修人员带来的集中荷重等组成。

上述作用荷重通过装置的连接传递及相互影响,将作用效果直接反映在各构件上,考虑的作用效果为叠加,作用方式按可能存在的最不利情况处置,按满足正常行车工作状态及极限作用效应两种方式,对构件的动强度和动刚度进行检算。

3 有限元瞬态响应分析基础理论

n自由度线性时不变振动系统结构,其动力学分析的有限元方程为

[M]{Δ″(t)}+[C]{Δ′(t)}+[K]{Δ(t)}={F(t)}

(1)

式中,[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{F(t)}为激励向量；{Δ(t)},{Δ′(t)},{Δ″(t)}分别为响应位移、速度和加速度向量。

用有限单元法求解结构的动力响应问题,有振型叠加法和逐步积分法。振型叠加法求解动力响应问题精度高,逐步积分法对能激起高阶分量的冲击问题则能达到较高精度。在正常工作条件下,接触网支持悬挂系统不会承受较大的冲击情况,因此,本文选用振型叠加法。振型叠加法又称为模态叠加法,其基本思想是将问题变换成解一组独立的微分方程,每个自由度有一个方程,求出每个方程的解,即各阶的响应,然后将结果叠加在一起得到整个问题的解。

用振型叠加法来求解动力学响应,首先必须求出结构无阻尼自由振动下的特征值w2(即固有频率)和特征向量{Δ0}(即振型)。设结构的前m阶固有频率为w1,w2,…,wm,对应的特征向量为{Δ0}1,{Δ0}2,…,{Δ0}m,以此构造振型矩阵

[Φ]=[{Δ0}1{Δ0}2…{Δ0}m]

(2)

将结构的位移响应表示为各振型的线形叠加

{Δ(t)}=[Φ]{y(t)}

(3)

式(3)中,{y(t)}为各模态的幅值向量,可看作为广义位移。将式(3)代入(1),得

[M][Φ]{y″(t)}+[C][Φ]{y′(t)}+

[K][Φ]{y(t)}={F(t)}

(4)

(5)

可得

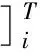
(6)

令

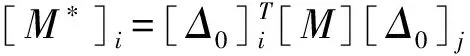
则式(6)可简写为

[M*]{y″(t)}i+[C*]{y′(t)}i+

[K*]{y(t)}i={F*{t)}

(7)

其中,i=1,2,…,m。式(6)可表示为

{F*(t)}/[M*]i(i=1,2,…,m)

(8)

式中，wi为第i阶的固有频率；αi为第i阶的阻尼比。

式(7)与式(8)相当于一个自由度系统的动力响应方程。求解单自由度系统的动力响应问题可以利用杜哈美积分。在求得各阶响应后,再进行叠加,最终求得结构的响应。

4 接触网的动力有限元分析

采用ANSYS10.0建立接触网支持装置的有限元模型。

4.1 接触网支持架模型的简化

建立准确而可靠的结构有限元计算模型,是一项最为重要的工作,它关系到计算结果的正确与否。一般来说,单元划分密可以减少有限元解的离散误差,但会增加建模工作量、计算机内存和计算时间,且计算结果数据的分析处理工作量巨大。实际工程问题非常复杂,支撑边界形式多样,因此就要求在建立计算模型过程中,进行必要的合理简化。鉴于三角支持装置的连接及结构特征,可采用杆件简化的一般原则,将载荷作用点转移到杆轴线上。

4.2 单元选择

在利用ANASYS对支持悬挂系统进行有限元模型的构建的过程中,虽然各种模型的结构有所差异,但是单元的选择却是相同的。由支持悬挂系统的结构特点可将原结构简化为一个以梁单元、管单元和杆单元构成的有限元模型。腕臂支持装置整体可以作为梁单元处理；棒式绝缘子、腕臂以及压管、定位管的部件的结构特点和受力情况可以作为管单元Pipe16处理；定位支撑只受轴向拉、压力,按杆单元Link8处理,故选取线单元。如图2所示,建立了两档65 m间距的接触线、承力索与吊弦组成的分布参数模型。

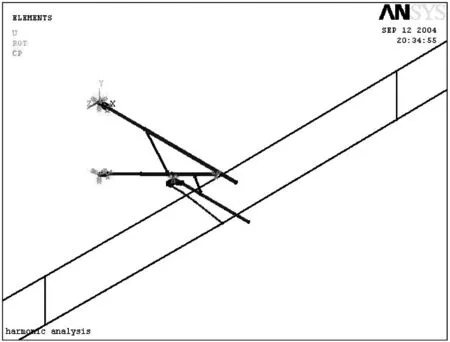
图2 两档距接触网的有限元模型

4.3 材料模式及其特性参数

支持装置静力模型中有以下三种材料模式。

腕臂为20号钢,弹性模量E=2.01×1011MPa,泊松比μ=0.3,密度ρ=7.85×103kg/m3。

绝缘子为瓷,弹性模量E=0.55×1011MPa,泊松比μ=0.2,密度ρ=3.1×103kg/m3。

定位器为6028铝合金,弹性模量E=0.70×1011MPa,泊松比μ=0.5,密度ρ=2.7×103kg/m3。

接触线、承力索与吊弦的材料参数及截面参数：接触线为120 mm2银铜合金,E=1.3×1011MPa,单位长度质量=1.08 kg/m；承力索为95 mm2铜合金绞线,E=1.3×1011MPa,单位长度质量=0.845 kg/m；吊弦为10 mm2铜合金绞线,E=1.3×1011MPa。

4.4 外载条件

接触网动载包括两个部分：受电弓作用在接触网上的抬升力和风载荷。其中受电弓的抬升载荷是铁路接触网设计中的常规问题,这里仅对风载进行说明。

计算工况：支架外悬长度3.1 m,结构高度1 400 mm,由承力索95 mm2+接触线120 mm2组成的简单链型悬挂中间柱装配,研究跨距65 m,风速35 m/s。结构上加垂直于导线方向的均布风载,以接触网工作环境中气候条件下最大的风速风载为加载依据。稳定风速下线索单位风载计算公式如下

P=0.613×10-3v2·CX

(9)

式中，P为线索单位面积风载，kN/m2；CX为风载体型系数,简单链型悬挂体型系数取1.25；v为计算风速，m/s。

支持架在一次列车通过这一时间历程内的瞬态风载分析。计算时间为50 s,稳定风压力为0.94 kPa。

5 结果分析与结论

图3所示为有限元计算获得的高应力区的节点的应力-时间历程。

图3 动应力响应曲线

在t=15 s时,支持架最大动应力为24 MPa,最大动挠度为1.73 mm。由此可知,支持架在风载和工作载荷同时作用下,动强度和动刚度均满足要求。

尽管本文仅提供一种工况的研究实例,事实上本文所提出的建模理论和单元选择思路,以及利用有限元手段,对其他受力元件或构件分析应用同样适用。

[1]易 日.使用ANSYS 6.1 进行结构力学分析[M].北京：北京大学出版社，2002.

[2]德Kieβling Puschmann，等.电气化铁道接触网[M].电气化工程局，译.北京：中国电力出版社,2004.

[3]〔苏〕И.И.符拉索夫.接触网[M].北京：中国铁道出版社，1986.

[4]魏明钟.钢结构[M].武汉：武汉理工大学出版社，2002.

[5]于万聚.交流电气化铁道接触网设计基础[M].北京：中国铁道出版社，1988.

[6]于万聚.电气化铁路接触网CAD系统[M].成都：西南交通大学出版社，1998.

[7]TB10009—2005，铁路电力牵引供电设计规范[S].

[8]王守礼.电力气候[M].北京：气象出版社，1994.