以基于孔隙结构特征的EPDM绝热材料热化学烧蚀模型①
李 强,冯 茵,李 江,杨 飒
(西北工业大学燃烧、流动和热结构国家级重点实验室,西安 710072)
0 引言
火箭发动机内绝热材料烧蚀机理及其计算模型一直是研究人员最为关心的核心问题之一[1]。在过去的几十年里,研究人员针对绝热材料烧蚀机理开展了大量的理论和实验研究,并建立了诸多数学模型及相应计算方法[2-3],但随着实验测量手段的日益发展,新的现象和规律必将被发现。以EPDM类绝热材料为例,通过对绝热材料烧蚀后形成的炭化层进行断面电镜扫描发现,其炭化层的结构为典型的蜂窝状多孔结构,丁腈橡胶类绝热材料也是如此。而以往烧蚀模型均忽略了这一重要结构特征,将炭化层等效为一种结构致密的物质,热解层产生的热解气体在流经炭化层时,不与炭化层内的C元素发生化学反应,主流燃气和热解气体中的氧化性成分在炭化层上表面和C元素反应,形成对炭化层的消耗,炭化层的线烧蚀率和质量烧蚀率是等效的。气流剥蚀和粒子侵蚀对炭化层烧蚀的影响,只能通过经验修正予以考虑。这样形成的结果是绝热层烧蚀计算模型人为修正参数多,计算模型通用性和计算结果可靠性差。
文中从炭化层微观孔隙结构特征出发,建立了基于炭层孔隙结构特征的EPDM材料热化学烧蚀模型和计算方法,为进一步建立热化学烧蚀、粒子侵蚀和气流剥蚀相耦合的通用绝热层烧蚀模型打下基础。
1 实验研究
炭化层电镜扫描照片如图1所示。

图1 炭化层电镜扫描照片Fig.1 SEM of charring layer
研究表明,绝热层的烧蚀机理主要包括热化学烧蚀、气流剥蚀和粒子侵蚀。其中,热化学烧蚀是基础,该过程以体烧蚀方式消耗炭化层,使其变得更加疏松,强度削弱;气流剥蚀和粒子侵蚀以作用力方式对炭化层形成机械破坏和消耗[4-5],炭化层是三者联系的纽带和桥梁。所以,对热化学烧蚀作用下炭化层结构特征的表征和演化过程的建模至关重要,文中主要针对绝热层的热化学烧蚀过程开展研究。
为给模型的建立提供实验依据和校验数据,首先开展了绝热层烧蚀实验研究。实验用烧蚀发动机结构如图2所示,8块EPDM绝热材料试件放置于试验段内。
实验采用燃温为3 280 K、含铝量为1%的复合推进剂,燃烧室平衡压强为5.9 MPa,总工作时间9.1 s。
计算结果表明,实验中绝热层试件表面的气流速度为2.4m/s。

图2 实验发动机结构示意图Fig.2 Schematic of ablation experiment motor
图3给出了烧蚀后的绝热层试件断面照片,其结构呈现典型的3层结构。图4给出了炭化层的电镜扫描照片。由图4可看出,炭化层属于典型的多孔介质,其表面没有明显的沉积物存在,炭化层上部的孔隙直径较大,结构相对疏松,下部孔隙直径较小,结构相对致密。对炭化层采用气体吸除法进行了孔隙率测量。结果表明,炭化层的平均孔隙率约为80%。

图3 绝热材料断面照片Fig.3 Cutting p lane o f ablativemateria l
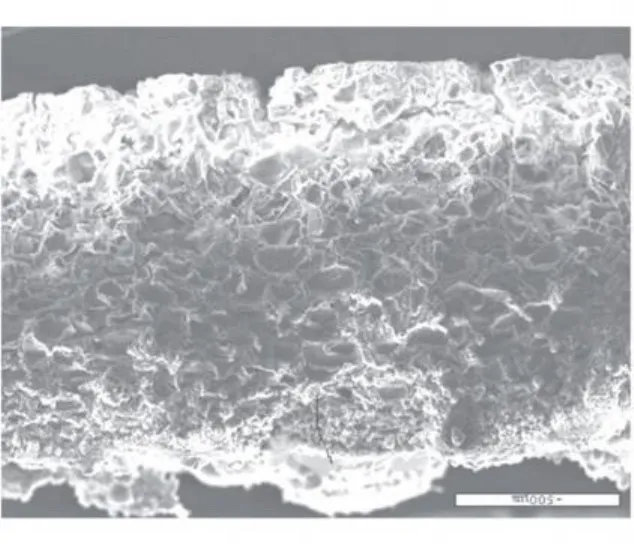
图4 炭化层电镜扫描照片Fig.4 SEM of charring layer
对炭化层的组分开展了能谱分析。结果表明,炭化层主要构成为C、O、Si 3种元素。图5为沿烧蚀方向炭化层不同位置处3种元素摩尔含量分布。由图5可看出,C、O、Si三者含量达95%以上;沿烧蚀方向,不同元素摩尔含量分布存在明显差异。这充分说明炭化层内部的化学烧蚀过程属于典型的体烧蚀,化学反应发生在多孔炭化层所占据的整个空间内。

图5 沿烧蚀方向不同组分摩尔百分含量分布Fig.5 Speciesmole fraction distribution along ablation direction
2 物理模型
基于以上实验结果分析,文中所建立的EPDM绝热材料热化学烧蚀模型仍采用传统的3层模型。模型的创新之处在于对炭化层的描述将突破以往对炭化层的定义,从炭化层的孔隙结构入手,建立基于炭化层孔隙结构特征的热化学体烧蚀模型。
各层描述如下:
(1)基体层。此层没有任何化学反应,仅有热传导。
(2)热解层。高聚物在此层裂解放出热解气体,并流向炭化层,存在高聚物裂解、热解气体流动和热传导,其厚度由材料的热解温度和炭化温度决定。
(3)炭化层。属于典型的多孔介质,热解气体和主流燃气在其内部扩散,并和炭化层骨架之间进行热交换;在多孔的炭化层内部,氧化性组分和多孔炭化层骨架中的C元素在骨架表面发生异相化学反应,消耗炭化层,使其孔隙率增大,形成质量烧蚀,同时强度减弱;当炭化层的孔隙率大于临界孔隙率(0.99)时,炭化层骨架消失,形成线烧蚀。
在以上模型中,假定:
(1)多孔炭化层中流动通道是相互连通的。通过对炭化层粉碎前后体积进行测定,表明炭化层内孔隙的开孔率达到78%以上,闭孔率不足2%,该假设成立。
(2)孔隙的特征尺寸远大于气体分子的平均自由量程。炭化层电镜扫描照片表明,炭化层的当量孔隙直径是微米级的,而炭化层中的气体分子多为小分子,如CO2、CO、H2O、O2等,其自由程为分子直径的10倍,远小于炭化层的当量孔隙直径,所以该假设成立。
(3)孔隙的特征尺寸充分小。
3 数学模型
对以上物理模型进行数学建模的核心是针对多孔结构炭化层内流动和传热的建模和求解,文中在建模中假设:
(1)炭化层骨架结构和气体之间始终处于当地热平衡状态;
(2)孔隙结构内的流动属于不可压缩流动;(3)各组元气体状态服从理想气体状态方程。
3.1 多孔介质内流动和传热控制方程及其数值求解方法
从质量守恒、动量守恒和能量守恒基本原理出发,通过积分平均可得到多孔介质内流动和传热的宏观控制方程[6]。
连续方程:

能量方程:

动量方程:

式中 ui为i方向的速度分量;ε为多孔介质的孔隙率;ρf、cpf和p分别为流体的密度、比热容和压强;υ为流体的层流粘性系数;K采用Ergun定律计算;Pre为层流Prandtl数;Sh为当地热源;Hc为计算单元内炭化层骨架和气体热容之比;
组分扩散方程:

式中 fi为第i种组分的质量百分数;D为组分扩散系数,由菲克扩散定律确定为第i种组分的质量生成率;ρ为气体密度。
以上描述多孔介质内流动与传热的质量、动量和能量守恒方程,可写成统一形成的广义输运方程:

式中 φ为广义输运变量;ξ为时间因子;Γ和S分别为广义扩散系数和广义源项[6]。
计算中,采用二阶全隐格式对广义输运方程进行离散,在交错网格上采用SIMPLE方法进行数值计算。
3.2 热化学反应模型
计算中,热化学反应采用传统的三步化学反应模型:

其中,化学反应速率由化学动力学控制。
根据Arrhenius公式,可得各气相组分的消耗率和炭的消耗率。

式中 A1、A2、A3和E1、E2、E3分别为对应于上面3个反应方程的指前因子和反应活化能[2];pi为气体组分i在炭化层孔隙内的分压。
在此基础上,根据质量守恒定律可由n时刻炭化层的孔隙率εn和炭化层骨架的比表面积Ψn,计算出n+1时刻炭化层的孔隙率εn+1:
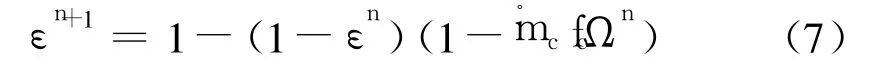
式中 fc为计算单元内炭化层骨架内C元素的质量百分含量。
以上计算过程中,还需计算n+1时刻炭化层的比表面积Ψn+1。为此,采用气体吸除法对不同孔隙率条件下炭化层的比表面积进行了测量,得到炭化层比表面积随孔隙率的变化曲线,如图6所示。计算中,在获得了n+1时刻炭化层的孔隙率εn+1之后,可通过插值计算出n+1时刻炭化层的比表面积Ψn+1。

图6 炭化层比表面积随孔隙率的变化曲线Fig.6 Variation of specific area along with porosity of charring layer
4 计算结果分析
采用以上的数学模型,针对实验开展了绝热层烧蚀数值计算。计算区域取2.0 cm×1.0 cm的矩形区域,初始时刻绝热材料的孔隙率为0.0,温度为293 K;炭化层的初始孔隙率由绝热材料热解过程中温度达到炭化温度时的残余质量计算。
表1给出了计算结果和实验结果的对比。由表1可看出,计算结果和实验结果较为接近,绝热材料炭化率和质量烧蚀率的相对误差均为20%,炭化层厚度的相对误差约为14.3%。计算结果中,绝热材料的炭化率、炭化层厚度均小于实验结果,质量烧蚀率略大于实验结果。

表1 计算结果和实验结果对比Table 1 Comparison between experimental and numerical data
图7给出了实验试件炭化率和质量烧蚀率随时间的变化曲线。由图7可看出,在绝热材料开始受热时,材料的炭化率和质量烧蚀率相对较大,分别达到0.25 mm/s和0.35 kg/(s·m2)。分析认为,这主要是因为在材料受热的初始时刻,绝热层表面温度相对较低,造成对流换热的热流密度相对较大,以及材料内部的升温速率较快造成的;3 s以后,材料的炭化率和质量烧蚀率逐渐趋于稳定状态,炭化率约为0.12mm/s,质量烧蚀率约为0.12 kg/(s·m2)。
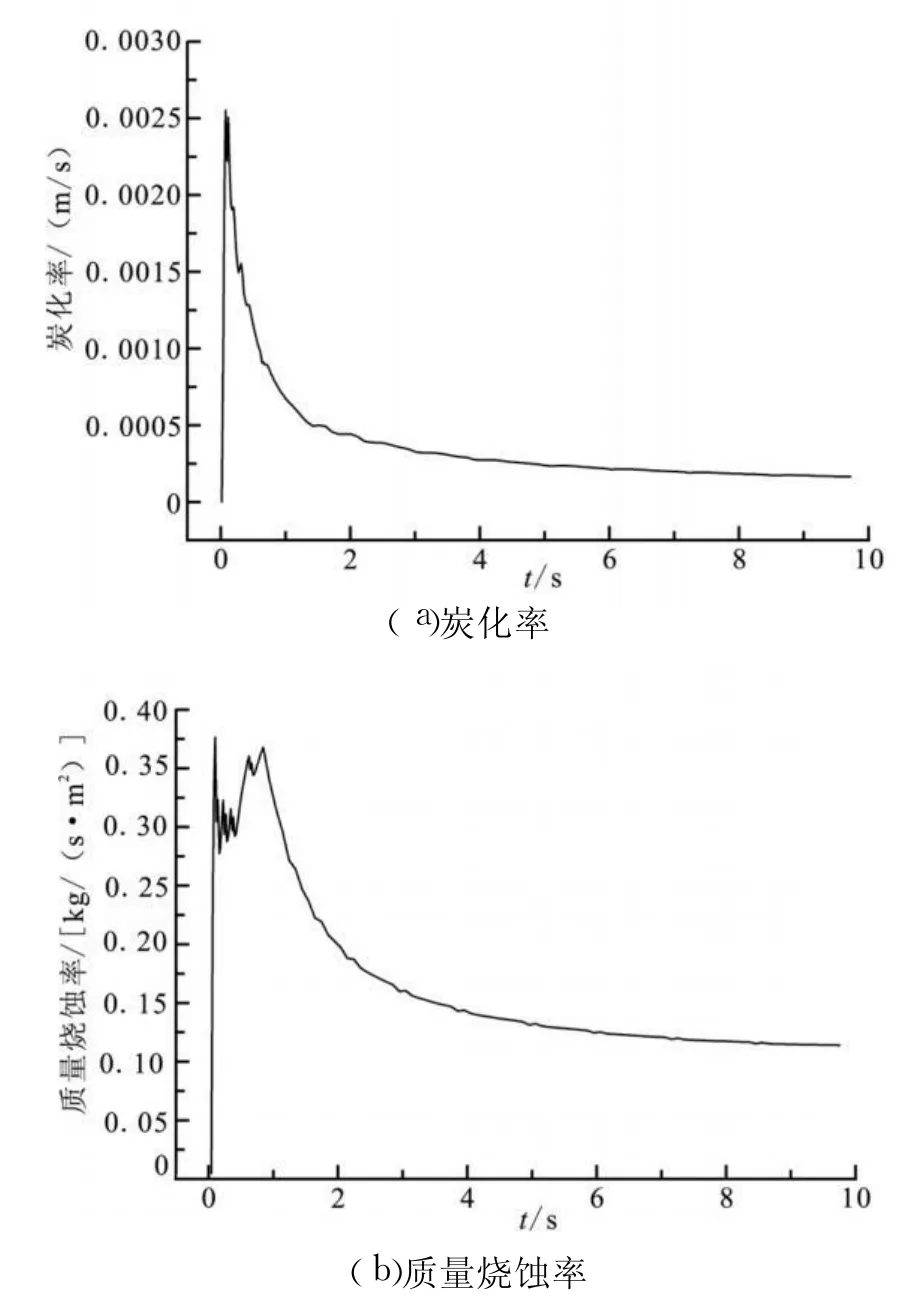
图7 炭化率和质量烧蚀率计算结果Fig.7 Simulated history of charring rate and ablation mass rate
图8给出了计算结果中材料内部孔隙率的分布云图。

图8 炭化层孔隙率分布云图Fig.8 Distribution of porosity in charring layer
由图8可看出,绝热材料烧蚀面上的孔隙率约为0.98,沿烧蚀面向下,孔隙率逐渐减小,该分布规律与炭化层电镜扫描照片的直观规律相同,孔隙率在炭化层的底部减小到0.73,在热解层和炭化层的交界位置,孔隙率从0.005突跃到初始孔隙率0.73,对炭化层内孔隙率进行体平均积分,可得炭化层内的平均孔隙率约为0.81,这与实验测量到的炭化层的平均孔隙率接近,表明文中模型和算法可信。
5 结论
(1)EPDM类绝热材料烧蚀后的炭化层属于典型的多孔介质,其热化学烧蚀过程分布于炭化层所占据的空间内,属于典型的体烧蚀。
(2)基于炭化层空隙结构特征建立的绝热材料热化学烧蚀模型更符合实际状况,计算结果可信。
[1] Yury I Dimitrienko.Modeling of erosion combustion of energetic materials in high-enthalpy flows[R].R&D Corporation“NPO Mashinostroenia”Gagarina,Reutov,Moscow Region,143952,Russia.
[2] 何洪庆,等.EPDM的烧蚀模型[J].推进技术,1999,20(4).
[3] 孙冰,等.冲压发动机燃烧室热防护层烧蚀计算[C]//中国宇航学会固体火箭推进专业委员会2001年年会论文集,2001.
[4] Koo JH,Lin S,Kneer M.Comparison of ablativematerials in a simulated solid rocket exhaust environment[R].AIAA 1991-0978.
[5] Yang B C.A theoretical study of thermo-mechanical erosion of high-temperature ablatives[D].The Pennsylvania State U-niversity,1992.
[6] Akira Nakayama.PC-aided numerical heat transfer and convective flow[M].CRC Press,Boca Raton,London.

