一般情况下磁场强度矢量切向分量跃变的讨论

付长宝，顾佳佳，李恩奎

(通化师范学院 物理系，吉林 通化 134002)

1 回顾矩形回路所在面为电流的垂面时磁场强度矢量切向分量的跃变关系

在积分形式的麦克斯韦方程组[1-5]中关于磁场强度矢量的环路积分方程为

(1)

方程(1)可用于讨论在两个介质分界面两侧的磁场强度矢量的切向跃变关系.如图1所示

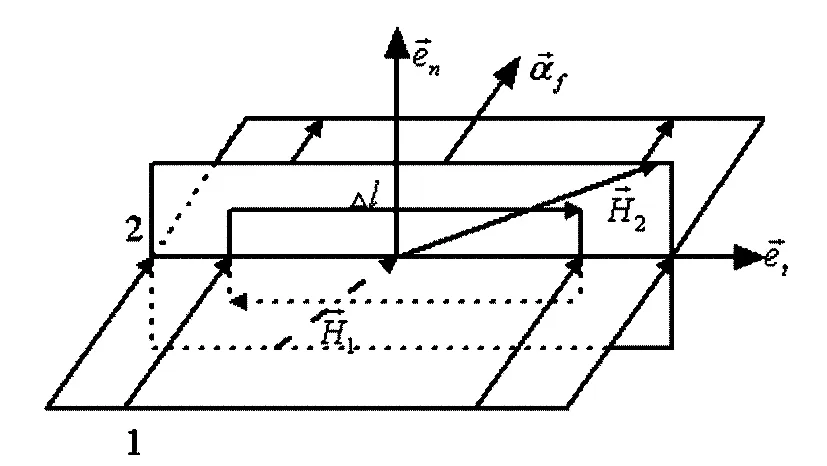
图1 矩形回路所在面为电流的垂面

(2)

If=αfΔl

(3)

→0

(4)

把方程(3)和(4)代入方程(1)中的右边，且考虑方程(2)得：

H2t-H1t=αf

(5)

由方程(5)可知若在介质分界面存在面电流分布，且矩形回路所在面为电流的垂面时，在介质分界面两侧磁场强度矢量切向分量是跃变的，跃变规律满足方程(5).

所用品种为京甜3号，采收当天运回实验室，挑选大小均一，无病虫害、无机械损伤、成熟度均匀的新鲜的青圆椒为试材。

2 讨论一般情况下磁场强度矢量切向分量的跃变关系

2.1 电流与矩形回路所在平面不垂直时磁场强度矢量切向分量的跃变关系

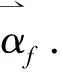
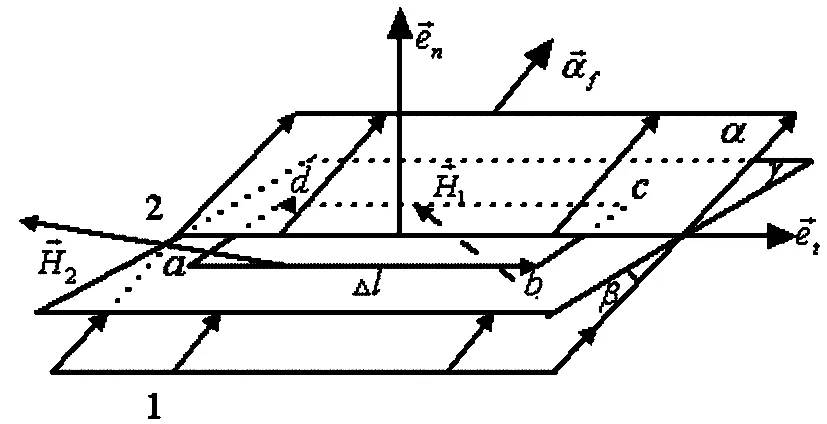
图2 电流与矩形回路所在平面不垂直

(6)

若考虑回路短边长度可看作趋于零，方程(6)可化简为：

(7)

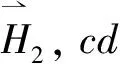
(8)

通过回路内的总自由电流强度为：

If=αfΔl

(9)

电位移矢量对矩形回路的通量变化率为：

→0

(10)

将方程(8)、(9)、(10)代入方程(1)得电流与矩形回路所在平面不垂直时磁场强度矢量切向分量的跃变关系：

H2t-H1t=αf

(11)

通过对比方程(5)和方程(11)可发现，当电流与矩形回路所在平面不垂直时磁场强度矢量切向分量的跃变关系与矩形回路所在面为电流的垂面时磁场强度矢量切向分量的跃变关系是一致的.

2.2 矩形回路所在平面与电流的垂面成某一角度时磁场强度矢量切向分量的跃变关系

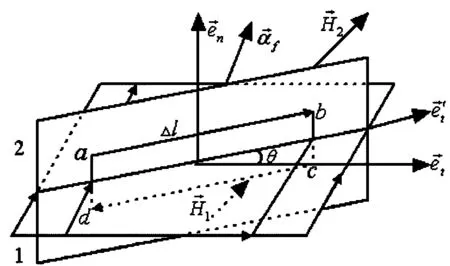
图3 矩形回路所在平面与电流的垂面成θ角

(12)

若考虑回路短边长度可看作趋于零，方程(12)可化简为：

(13)

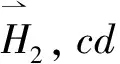
(14)

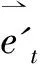
If=αfΔlcosθ

(15)

电位移矢量对矩形回路的通量：

→0

(16)

将方程(14)、(15)、(16)代入方程(1)中即可得到矩形回路所在平面与电流垂面成某一角度时磁场强度矢量切向分量的跃变关系：

(H2t-H1t)=αfcosθ

(17)

通过对比方程(5)和方程(17)可发现矩形回路所在平面与电流垂面成某一角度时，磁场强度矢量切向分量的跃变关系与矩形回路所在面为电流的垂面时磁场强度矢量切向分量的跃变关系是不同的.

若综合考虑由2.1与2.2所形成的一般情况，磁场强度矢量切向分量的跃变关系与方程(17)是一致的.

3 结论

综上所述，本文根据文献[1-5]讨论了一般情况下磁场强度矢量切向分量的跃变关系，从而获得了一般情况下磁场强度矢量切向分量的跃变关系，通过比较发现一般情况下磁场强度矢量切向分量的跃变关系与矩形回路所在面为电流垂面时获得的磁场强度矢量切向分量的跃变关系是不同的.

参考文献：

[1]郭硕鸿主编.电动力学[M].高等教育出版社，1997.

[2]汪德新.电动力学简明教程[M].科学出版社，2005.

[3]尹真.电动力学[M].科学教育出版社，2005.

[4]付长宝，沈慧娟，杨光英.磁场矢量边值关系的讨论[J].通化师范学院学报，2008(8).

[5]蔡圣善，朱耘，徐建军.电动力学[M].高等教育出版社，2002.