多层湍流大气相位屏的数值模拟

付 玉，金振宇

(中国科学院国家天文台/云南天文台，云南 昆明 650011)

由于湍流大气的干扰，严重影响大型地基望远镜的成像，使天文目标长曝光图像的空间分辨率[1]下降。高分辨统计重建技术[2-4]和自适应光学技术[5]可以有效消除湍流大气的影响，重建天文目标的高空间分辨率图像。但是等晕区效应限制了成像视场角的大小。所谓的等晕区[6]，是指当天文目标相对于望远镜的张角很小，以至于目标的所有部分受到了相同的大气扰动的影响，目标的成像区域具有相同的瞬时点扩展函数，一般情况下，等晕区会小于5″[7]。当观测目标的视场比较大时，目标的不同部分受到了不一致的大气扰动，大气—望远镜综合系统不再是线性空不变的。因此为了实现太阳等视场角比较大的天文目标的高分辨重建，需要深入研究等晕区对各种高分辨重建方法的影响以及消除等晕区效应的方法。天文实测由于受到仪器噪声、望远镜像差和其他一些无法预料的干扰因素的影响，而单独提取等晕区的效应进行研究是有些困难的，因此数值模拟是比较有效的研究手段。

目前有几种随机大气相位屏的数值模拟方法，如FFT功率谱反演法[8]、Zernike多项式法等[9]，这些方法将整个湍流大气等效为一层很薄的相位屏进行模拟。在不考虑等晕区效应的前提下，可以利用这些数值模拟方法研究和验证各种高分辨重建技术。但是利用这些方法不能很好地模拟等晕区效应，为此需要研究有效模拟等晕区效应的湍流大气相位屏的数值模拟方法。自适应光学技术为实现扩大等晕角一般采用多层共轭校正技术[10]，这项技术是根据高度对大气进行分层，对不同高度的湍流大气的波前畸变分别进行校正。受此启发，本文提出一种改进单层大气模拟的不太精确的方法，即对大气相位屏进行多层模拟，实现等晕区效应。类似于多层共轭校正技术，将大气分层，对各层大气分别进行数值模拟，并对不同入射角的光沿着传播路径进行积分，即可以得到每一个入射角的随机相位屏。关键的问题是如何对大气进行分层，如何确定每一层相位屏的等效高度和等效大气相干参数。本文具体介绍了多层大气模拟方法并给出了模拟实验的结果，利用斑点干涉术的运算结果验证了多层大气相位屏的模拟方法。

1 多层大气相位屏的模拟方法

1.1 大气分层

大气层的厚度在1000km以上，但没有明显的界限。整个大气层随高度不同表现出不同的特点[11]，分为对流层、平流层、中间层、暖层和散逸层，再上面就是星际空间了。对流层在大气层的最低层，紧靠地球表面，厚度约为10km到20km,是大气湍流强度变化最大的一层，而且受地理纬度、气候、温度等因素的影响较大。在对流层内，按气流和天气现象分布的特点又可分为下层、中层和上层。下层又称扰动层或摩擦层，其范围一般是自地面到2km高度，其中，从地面到200m高度又可以称作近地面层，也是受风速影响较大的一层；中层的厚度一般为6km到8km, 它受地面影响比摩擦层小得多；上层的范围可以从8km到10km的高度一直延展的对流层的顶部。根据对流层大气的特性将其分成4层，第1层是从0到200m，第2层是从200m到2km, 第3层从2km到10km, 第4层是从10km 到18km。

1.2 大气相干参数r0和等效高度

(1)

在自适应多层共轭波前校正技术[13]中，将每一层的湍流大气对光波的扰动看作是集中在薄薄的一层上，并且每一层大气都包含一个改正镜或者相位屏来校正该层大气引起的波面畸变。1994年，文[14]作者提出了相位屏位置设置的优化方案, 借鉴其思想确定模拟的每一层大气相位屏的高度，通过下面的公式：

(2)

来求解hi。其中，Hi-1和Hi分别表示一层大气的上下边界高度；hi表示该层大气相位屏的高度。依照同样的方法最终确定其他各个大气层的相位屏的高度。

1.3 HV/21模型

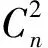
(3)

其中，V和A是自由参数，A表示近地面湍流强度，使用A=1.7×10-15m-2/3；V代表风速，在HV/21模型中[16]，V=21m/s。

1.4 模拟方法

模拟多层随机大气相位屏的目的是要模拟不同入射角的平面波的随机波前相位。因此首先模拟每一个分层大气相位屏后，沿着光波的传播路径对分层大气相位屏进行积分，从而获得不同入射角平面波的随机波前相位。

对每一分层大气相位屏的模拟，采用Zernike多项式方法。将畸变波前分解成圆域内正交的形式，通过大气湍流Kolmogorov谱的特性建立Zernike多项式各阶系数的协方差矩阵与大气相干参数r0的关系，就可以通过模拟多项式的系数生成具有不同的大气相干参数r0的随机大气相位屏。下面介绍如何得到不同入射角平面波的随机波前相位。

设4层等效相位屏的高度分别为h1、h2、h3、h4，模拟目标所需要的相位屏的尺寸由目标张角和最上层的大气相位屏的高度h4决定，如果目标的张角为θ，模拟的望远镜的口径为D，那么，每一层相位屏对应的实际尺寸至少应该为：

L=D+h4tanθ

(4)

不同入射角的平面波的传播路径计算是下一步的关键，假设入射角与望远镜光轴的角度为θi，则每一分层随机相位屏上的偏移量为：

Δli=hitanθi(i=1,2,3,4)

(5)

根据每一层大气相位屏的偏移量，沿着传播路径对多层大气相位屏进行积分，即可得到入射角为θ的随机相位屏。

2 多层大气相位屏的模拟结果

根据上面的分析，可以通过HV/21模型得到每一层湍流大气的大气相干参数和大气相位屏的等效高度，具体数值如表1。光波在整个传播路径上的r0的值可以用每一层的大气相干参数r0i表示。由HV/21模型和模拟的大气总高度决定总的大气相干参数r0=10cm,由于分层大气中每一层的大气相干常数与总的大气相干参数有这样的关系[11]：

(6)

N表示大气的分层数。

表1 四层大气的参数Table 1 The atmospheric parameters of four layers

按照表1中的参数值，采用Zernike多项式法分别生成4层随机相位屏，望远镜的口径为D=1m, 中心波长λ=550nm，望远镜的焦长f=133m。CCD的像元大小为32μm。

图1列出了光波以5″入射和垂直入射时对应的4层大气相位屏，从图1(a),(b)两组相位屏中可以看出每一层大气相位屏都有不同的偏移。

(a)垂直入射情况

(b)5″入射情况

Fig.1 Simulations of phase screens of four layers.In (a)or (b)phase screens of the first, second, third, and fourth layers are represented from left to right ,respectively. Pannels(a)and(b)are for incident angles of 90°and 0.5″,respectively

图2中斑点图分别是光波入射角度为0″、2″、5″、8″、10″时的斑点图。从模拟的斑点图可以看出随着入射角度的增加，斑点图相似性变差。

图2 模拟结果的示意图Fig.2 An array of simulation results of speckle images

3 模拟与实测结果的比较

斑点干涉术是一种基于频域变换的图像高分辨率重建算法，以大量的斑点图作为统计样本，很好地重建目标的功率谱和自相关像。因此，我们观测了4.5″的双星STF1110并模拟了5″和8″的双星，通过对比斑点干涉术处理的结果来验证多层大气模型。

利用得到的多层大气相位屏模型生成角间距为5″和8″的斑点图，以500幅作为统计样本，对其求平均功率谱，以其中的一颗星作为参考星退卷积，最终得到了目标的功率谱的重建结果。2008年9月，在云南天文台1m望远镜观测了角间距为4.5″的双星——双子座Alpha(STF1110)，大气相干参数r0约为10cm，采集了500幅斑点图。首先减去每一幅斑点图的暗场，同样对其进行统计平均，得到实测双星的重建的功率谱。

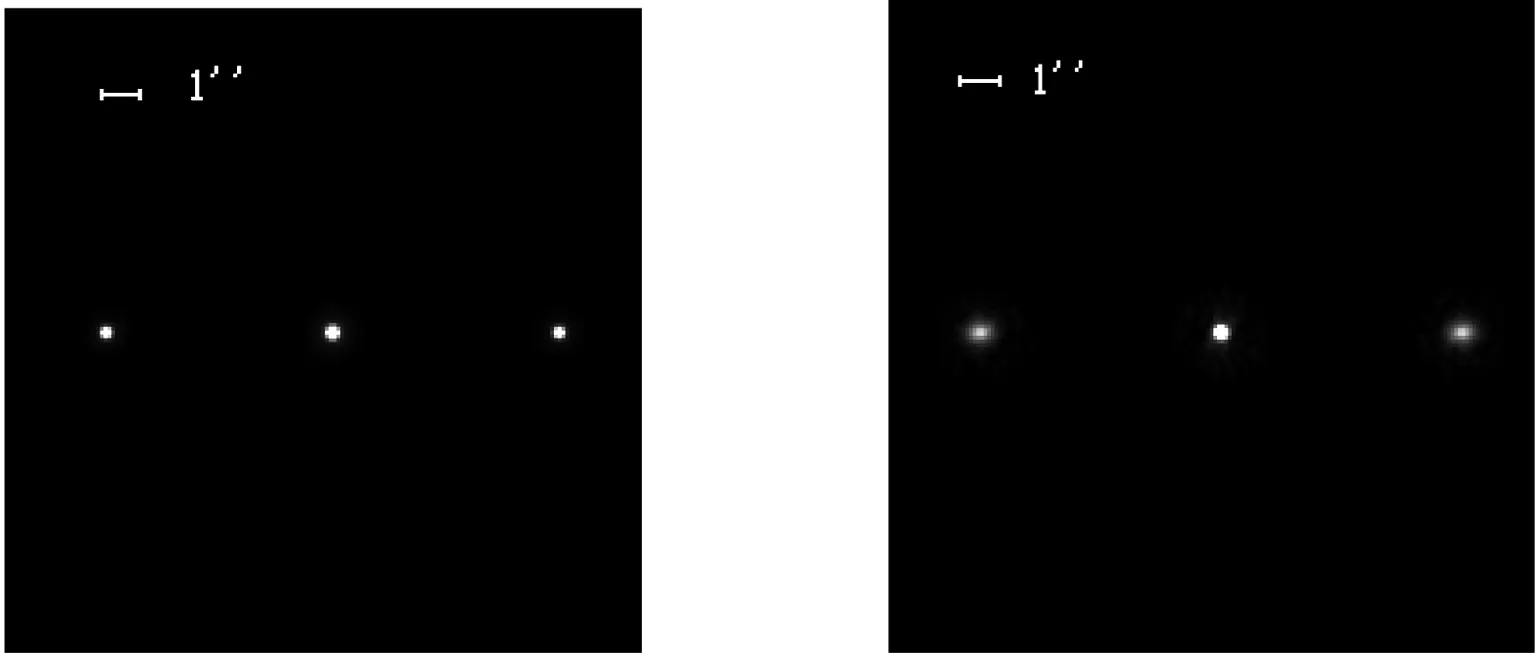
先看一下目标的自相关像的重建结果。以理想情况5″的双星的自相关像做对照，如图3(a)所示。图3(b)表示存在大气扰动时5″的双星的重建自相关像，可以看出图像变得模糊。图3(c)表示存在大气扰动时8″的双星的重建的自相关像，同时，重建了实测双星STF1110的自相关像。比较图3(b)、图3(c)和图3(d)，可以发现，模拟双星与实测双星的重建自相关像的表现形式有很大的相似性。

(a) (b)

(c) (d)

图3 双星的自相关像. (a)理想情况5″双星的自相关像(b)有大气扰动时5″的双星的自相关像的重建结果(c)有大气扰动时8″的双星的自相关像的重建结果(d)实测双星STF1110的自相关像的重建结果

Fig.3 The autocorrelation of binary speckles.(a)For a binary with a 5 arcsec separation and under the condition of no atmospheric turbulence.(b)Reconstructed autocorrelation of the same binary as in (a) but under the influence of turbulence.(c)Reconstructed autocorrelation of a binary with an 8 arcsec separation and under the influence of turbulence.(d)Reconstructed autocorrelation of the observation of the binary STF1110

模拟双星的功率谱的重建结果如图4和图5，其中的实线分别代表5″和8″的模拟双星在有大气扰动的情况下的功率谱的重建结果。为了比较，给出了5″和8″的双星的理想功率谱，以虚线表示。

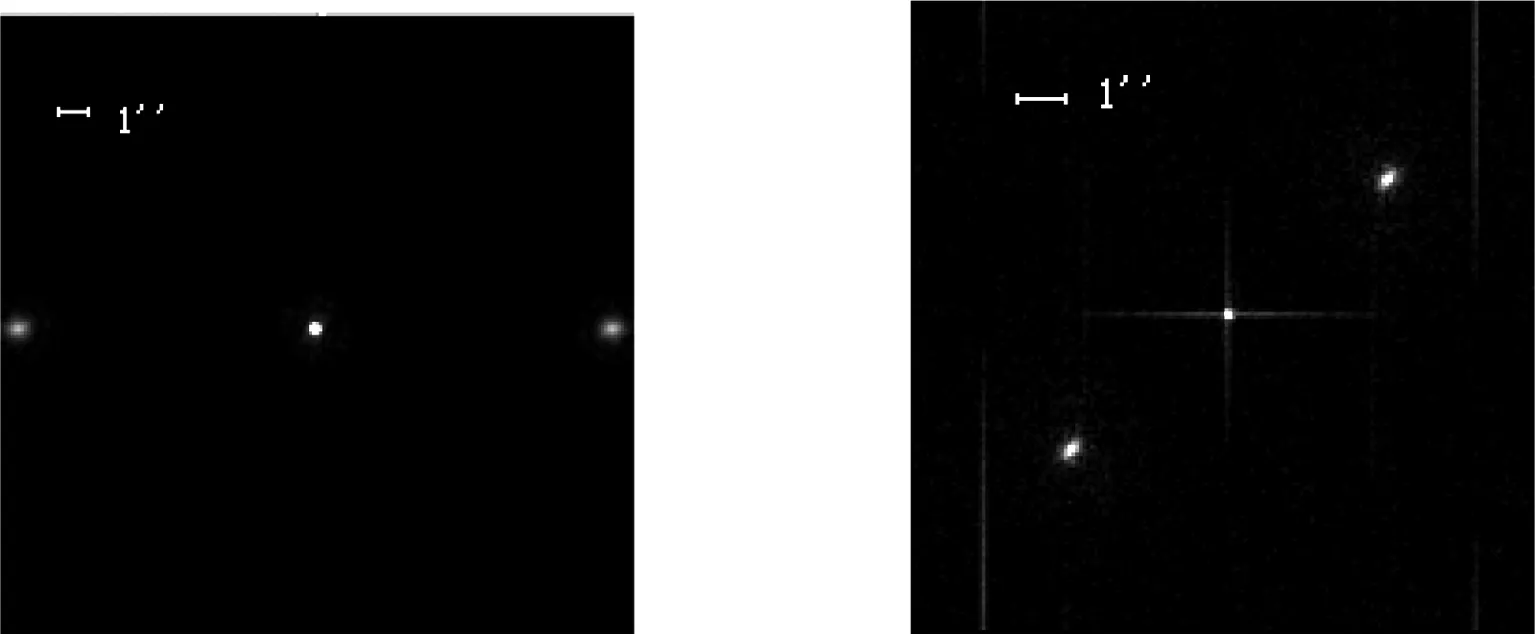
对于实测的目标双星STF1110，由于CCD的各种噪声的存在，望远镜像差、光谱带宽的影响，使得重建的双星功率谱在各个频率上都呈现了剧烈的起伏。如图6所示为实测双星STF1110的功率谱的重建结果，横坐标代表空间频率，纵坐标表示归一化的重建的目标功率谱。

从图3、图4、图5和图6中可以发现，模拟的双星和实测的双星经过斑点干涉术处理后都显现了等晕区带来的影响。模拟的5″和8″的双星与实测双星的重建的自相关像很相似，而从模拟的5″的双星的功率谱与实测的目标双星功率谱的重建结果中可以看出，双星功率谱特有的条纹都变得不清晰，特别是模拟的8″的双星的功率谱，相对于理想双星的功率谱更加表现出条纹不清晰，高频信息受到严重抑制现象。

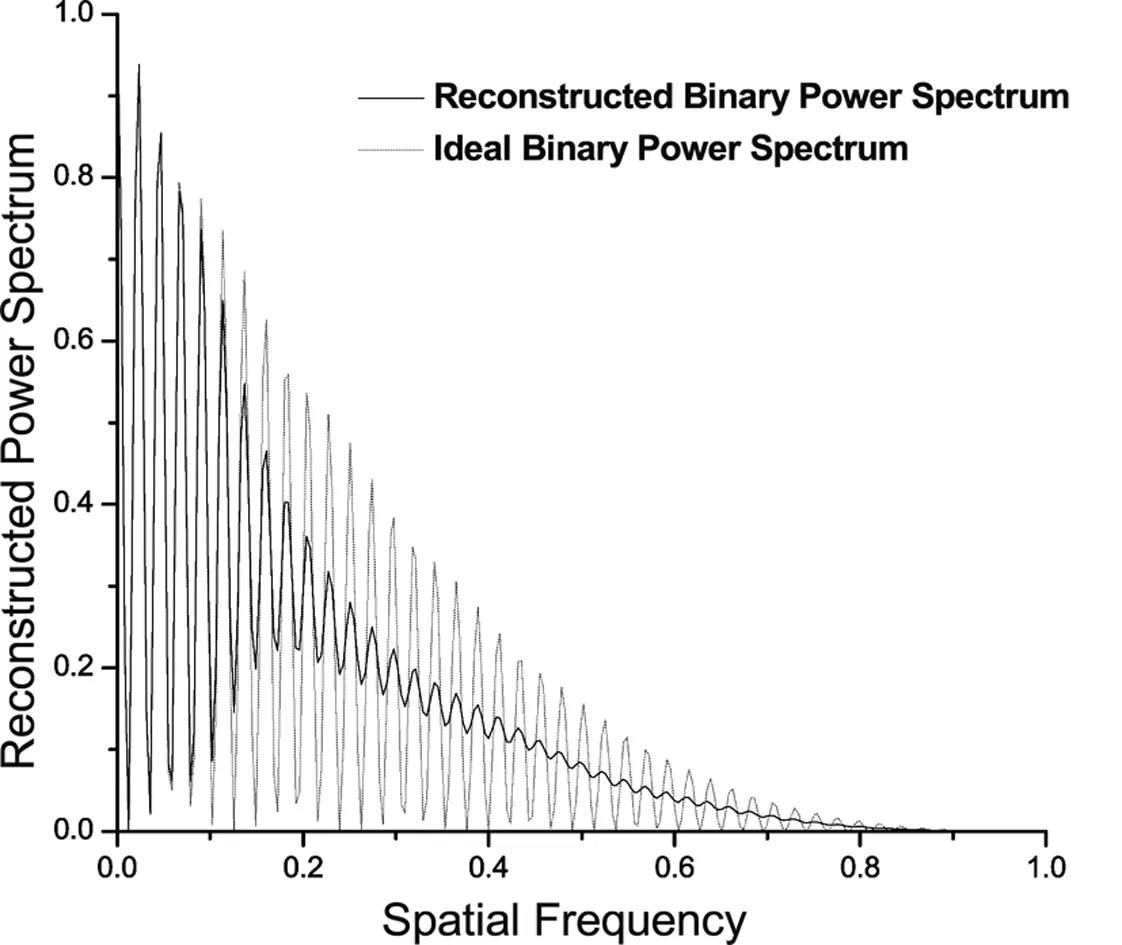
图4 模拟的5″的双星的重建功率谱，实线代表有大气扰动存在情况重建的双星的功率谱,虚线表示双星的理想功率谱

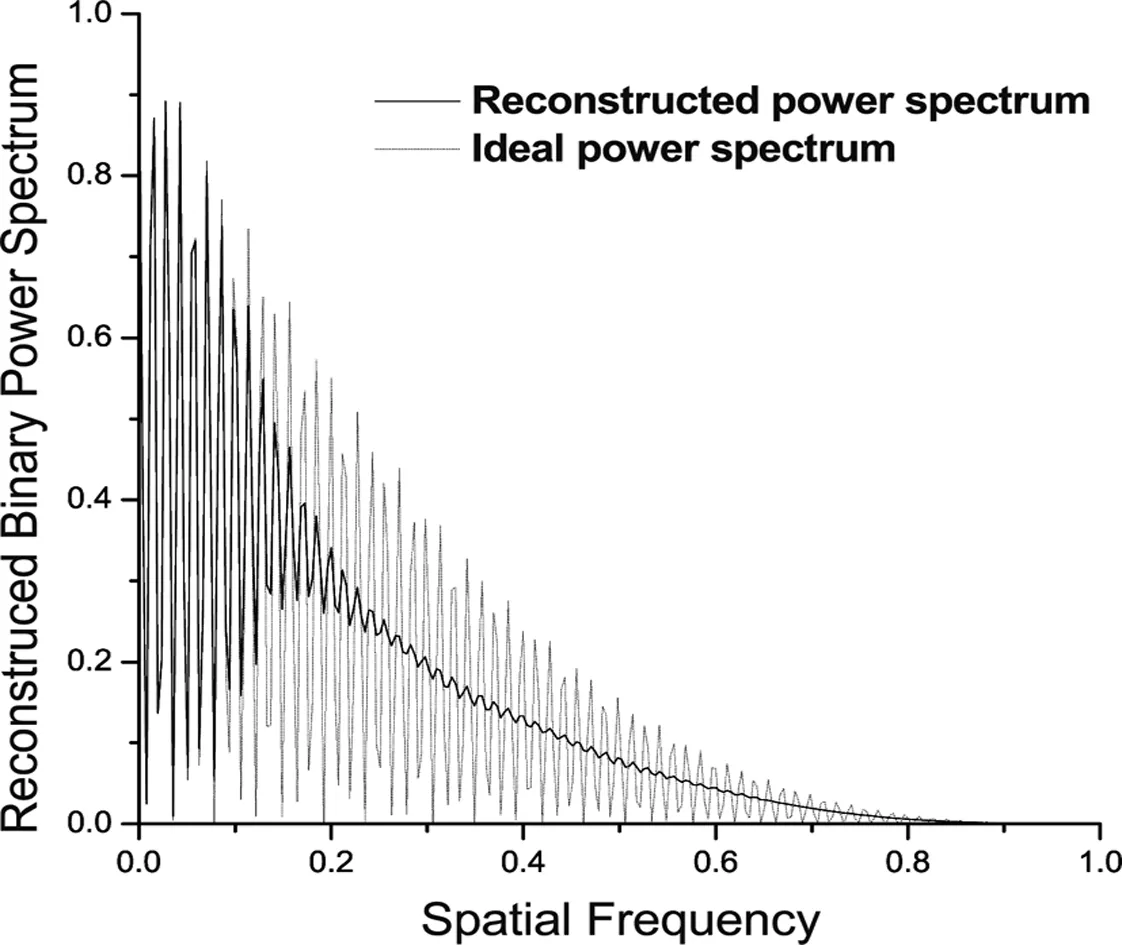
图5 模拟的8″的双星的重建功率谱，实线代表有大气扰动存在情况重建的双星的功率谱,虚线表示双星的理想功率谱

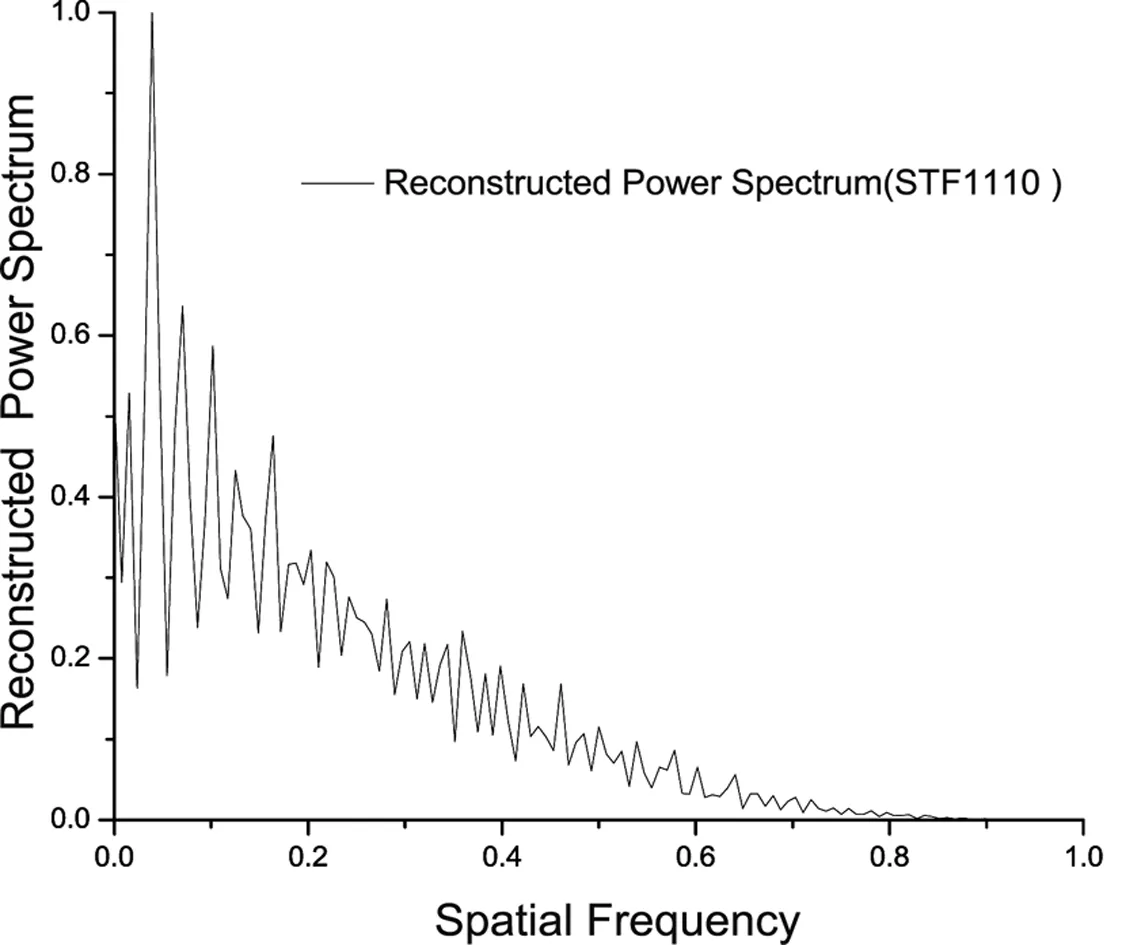
图6 实测目标双星STF1110功率谱的重建结果Fig.6 The reconstructed image power spectrum form the observation of the binary STF1110

4 总结与展望

利用数值模拟的方法构造了多层大气相位屏，能更好地模拟不同尺度的目标经过湍流大气成像。模拟双星和实测双星的斑点干涉术重建结果的对比分析表明，多层大气随机相位屏的模拟方法可以有效地模拟等晕区效应。这个方法既可以应用于等晕区对高分辨统计重建技术影响的研究中，也可以应用于自适应光学的多层共轭校正技术的研究中。

[1]D L Fried.Limiting Resolution Looking Down Through the Atmosphere[J].J Opt Soc Am,1966, 56：1380-1384.

[2]A Labeyrie.Attainment of diffraction-limited resolution in large telescopes by Fourier analyzing speckle patterns in star images[J].Astron Astrophys,1970,6:85-87.

[3]Liu Zhong,Qiu Yaohui,Lu Ruwei.Reconstruction of video images through turbulent atmosphere[J].Proc SPIE,1998,3561:326-331.

[4]邱耀辉，刘忠，卢汝为,等.天文图像空域重建新方法：迭代位移叠加法[J].光学学报，2001，21(2):186-191.

[5]M A van Dam,A H Bouchez,D Le Mignant,et al.The W.M.Keck Observatory Laser Guide Star Adaptive Optics System:Performance Characterization[J].Astr Soc Pac,2006,118:310-318.

[6]J W Goodman著，秦克成等译.统计光学[M].北京:科学出版社，1992，367-368.

[7]D L Fried.Anisoplanatism in adaptive optics[J].J Opt Soc Am,1982:72.

[8]MCGLAMERY B L.Restoration of turbulence-degraded images[J].J Opt Soc Am,1996,57:293-297.

[9]Robert J Nol1.Zernike polynomials and atmospheric turbulence[J].J Opt Soc Am,1976,66(3):207-211.

[10]Beckers J M. Detailed Compensation of Atmospheric Seeing Using Multi-conjugate Adaptive Optics[J].Proc SPIE,1989,1114:215.

[11]王亦.认识地球[M].北京：中国建材工业出版社，1998.

[12]Michael C Roggemann,Byron Welsh.IMAGING THROUGH TURBULENCE[M].1996.

[13]Beckers J M. Increasing the size of the isoplanatic patch with multiconjugate adaptive optics[C]//Ulrich M H.ed.Proc of the ESO Conference on Very Large Telescopes and Their Instrumentation Garching European Southern Observatory,1988:693-703.

[14]Edward P Wallner. Optimizing the locations of multiconjugate wavefront correctors[J].SPIE,1994, 2201:110-116.

[15]R E Hufnagel.Variation of Atmospheric Turbulence[C].Digest of Technical Papers,Topical Meeting on Optical Propagation through Turbulences,1974.

[16]Sergio Chueca,Begona Garcia-Lorenzo.Input parameters of the HV model above canarian observatories[J].SPIE,1994, 2201:159-166.