输电铁塔K节点变形的数理统计分析
李 强, 吴庆华, 徐志军
(1. 中南电力设计院, 湖北 武汉 430072; 2. 华中科技大学 土木工程与力学学院, 湖北 武汉 430074)
目前,输电铁塔无论是设计过程、加工过程或者是施工过程都有一套成熟的流程,这三个过程在理论上应该是环环相扣的,但在实际实施中却往往存在着较大的差别,尤其是在加工和施工过程中,由于人为和环境因素的影响,导致最终竣工的铁塔和设计图纸上的铁塔有一些差异,主要表现在发生了一定的变形,这些变形会给铁塔的性能造成一定影响。随着电力建设的飞速发展,工程中采用的铁塔数目大量增加,如何控制成批铁塔的设计、加工以及施工质量成为了一个重要的课题[1]。
陈建稳等人采用数值分析方法,对输电铁塔的内力和变形进行了分析[2, 3]。罗健明介绍了分析铁塔弯曲变形的基本方法,从多角度进行探讨,找出了产生弯曲变形的各种因素,供设计、制造和施工等有关部门参考[4]。陈海波根据两年多的塔基变形监测数据,分析了该铁塔变形治理的效果[5]。但是目前在输电线路的设计、加工以及施工过程中较少采用数理统计的方法。本文基于数理统计原理,针对某线路工程铁塔K节点变形问题应用数理统计等工具,进行了详细分析,并对送电线路中铁塔的变形进行了一些有意义的探讨。
1 理论依据
数理统计以概率论为理论基础,根据实验得到的数据,来研究随机现象,对研究对象的统计规律做出种种合理的估计和推测。在大量的随机试验中,各种试验结果的出现必然会呈现它们的规律性,因而只要对随机现象进行多次观察,这些规律就一定能清楚地呈现出来[6]。
1.1 均值μ的置信区间
(1)
此时,分布t(n-1)仅仅和n有关,因此可得
(2)
由此得到μ的置信水平为1-α的置信区间为
(3)
在实际工程中,总体σ2未知的情况很多,因此(3)式具有较大的实用价值。
1.2 假设检验
对总体的概率分布或分布的参数作某种假设,然后根据抽样得到的样本观测值,运用数理统计的分析方法,检验这种假设是否正确,从而决定接受或拒绝假设,这样的统计推断方法就是假设检验。样本X1,…,Xn来自正态总体X~N(μ,σ2),如果总体方差σ2已知,构造检验统计量[7]:
(4)
当μ=μ0时,Z服从N(0,1)。给定显著性水平α,则有
H0∶μ=μ0H1∶μ≠μ0
(5)
H0∶μ=μ0H1∶μ>μ0
(6)
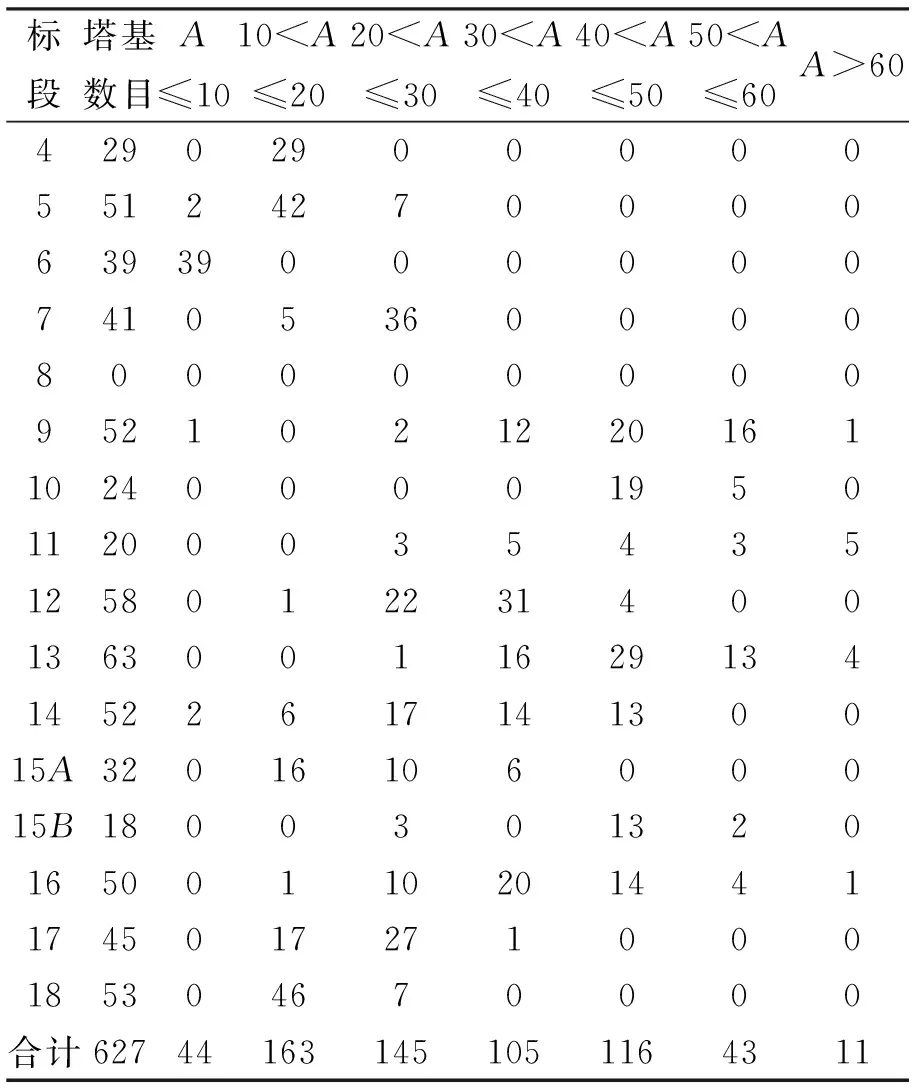
检验方法为:当z≥zα时,拒绝H0;当z H0∶μ=μ0H1∶μ<μ0 (7) 检验方法为:当z≤-zα时,拒绝H0;当z>-zα时,不能拒绝H0。 某线路工程在施工过程中,发现塔头K节点处(如图1所示铰接处)有一定的变形值。对其变形情况分标段按照架线前和架线后两种情况进行统计。 在数据的收集统计时,以下情况需要考虑:每个标段统计的数据都有不同的塔型,而且比例不一致。在通过对变形值进行理论计算后,发现不同型式杆塔的初始变形差别不大。真实的变形包括两个方面[8]:理论变形和由于螺栓直径比螺栓孔径小1~2 mm所引起的累积误差而引起的变形。由于实际变形比理论变形大很多,且不同塔型的理论变形相差不多;同时各个标段都有不同的塔型分布,且差别不大,因此本文假定变形值不受塔型变化影响。 图1 某线路工程“猫头塔” K节点 本文采用Kormoropob 的Dn 检验法[9,10]对架线前和架线后变形的统计数据进行正态性检验。通过计算表明,架线前后数据与正态分布吻合得较好。 架线前K节点位移统计情况见表1,表中A为变形值(单位为mm)。 对架线前变形的数据进行统计分析,变形值样本数为627个。 表1 架线前统计情况 由于n=627,样本数量非常大,由独立同分布的大数定理可以推导出方差值以及标准差。 方差σ2=S2=220.28 标准差σ=S=14.84 在满足概率为95%的前提下 同理,在概率为95%的前提下, 同时,在显著水平σ=0.05下,求出其均值的双侧置信区间。假设随机抽取至少45基铁塔,变形值服从正态分布。 统计情况见表2,经过统计得: 方差:σ2=S2=253.7 标准差:σ=S=15.9 在概率为95%的前提下,A值上限值是70.3,A值下限值是17.9。均值在显著水平α=0.05下的双侧置信区间为 (42.13,46.76)。 表2 架线后统计情况 假设H0:μ=μ0=29.42(即假设该段没有明显偏高); H1:μ>μ0(即假设该段明显偏高); 这是右边检验问题,其拒绝域为: 通过统计,可以从两方面进行分析,一是分析各个标段的差异性,进一步分析原因。二是通过整体分析,可以分析出理论变形以外的加工误差、螺栓孔径引起的变形等对节点变形的影响。 2.4.1影响变形的其他因素 架线前位移值小于52 mm的保证率为95%。计算理论位移值未架线时7~8 mm左右,从统计数据分析,全标段均值为30 mm,可以估计架线前各种误差对位移的影响约为22 mm左右。 架线后位移值小于70 mm的保证率为95%。计算理论位移值已架线时24 mm左右,从统计数据分析,全标段均值为45.49 mm,可以估计架线后各种误差对位移的影响约为21 mm左右。 架线前和架线后各种误差对位移的影响值都为21~22 mm左右,可见架线前、后理论计算差值是符合规律的。K节点架线前、后的位移控制值应取理论值加上误差值和其他影响值。 这里的差值主要原因是由于螺栓孔径的影响。在规范规程中,粗制螺栓孔径比螺栓大1~2 mm,由于整个塔架的连接都是由螺栓连接而成,大量的差值累计导致了这种变形。 2.4.2标段差异性 针对不同标段,可以分别对其进行统计分析,均值以及标准差能很好反映情况。标准差越大,表明其数据的离散度越大,由于每个标段的塔材都同样来自不同的塔厂,应该说,塔厂的影响因素是较小的。产生某些标段数据离散性较大的一个重要原因可能是施工的控制、管理因素。比如某些段,变形值的均值和方差都比其他段要大,这就需要从施工工艺、施工管理等方面找问题。 针对统计分析结果,制定了相应的措施。对于架线前变形大于50 mm以及架线后变形大于70 mm的部分铁塔进行了整改。经过整改后,工程投入运行,目前运行良好。 (1) 利用数理统计原理对铁塔K节点变形进行了分析,通过和理论计算的比较得出由于粗制螺栓孔径而引起的累积误差,并给出了差值的大小参考值,对于其他类似工程具有重要的参考意义。 (2) 利用数理统计的有关理论,给出了某工程K节点变形值的合理范围,具有一定的工程实际意义。 (3) 针对施工单位,给出了检验其施工工艺、水平的一个方法,通过和本单位前期工作或者其他标段施工单位比较,可以得到相应的假设检验,真正找到科学的评定方法,使得评定结果反映真实情况。 (4) 数理统计方法作为一种科学的数学工具,能够为工程实践提供科学的依据,可望在输电线路工程中进一步得到应用。 [1] 杨元春, 张克宝. 输电跨越塔设计回顾与展望[J]. 特种结构, 2006, 23(3): 70-76. [2] 陈建稳, 袁广林, 刘 涛. 数值模型对输电铁塔内力和变形的影响分析[J]. 山东科技大学学报(自然科学版), 2009, 28(1): 40-45. [3] 赵滇生. 输电塔架结构理论分析与受力性能研究[D]. 杭州: 浙江大学, 2003. [4] 罗健明. 对500kV铁塔斜材弯曲变形的分析[J].广西电力工程, 1996, (4): 53-56. [5] 陈海波. 急倾斜煤层采空区某铁塔变形治理与监测[J]. 岩土力学, 2003, 24(s2): 427-430. [6] 盛 骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京: 高等教育出版社, 1989. [7] Huang J, Wellner J A. Interval censored survival data: a review of recent progress [C] // Proceedings of the First Seattle Symposium in Biostatistics: Survival Analysis, Springer, 1997: 123-170. [8] Oran C. Tangent Stiffness in Plane/Space Frames[J]. Journal of Structure Division, ASCE, 1973, 99(3): 973-1001. [9] 庄楚强,吴亚森. 应用数理统计基础[M] . 广州: 华南理工大学出版社,2003. [10]R V 豪格,A T 克莱格. 数理统计导论[M] . 朱鋐宏道,译. 北京:高等教育出版社,1990.2 工程实例分析
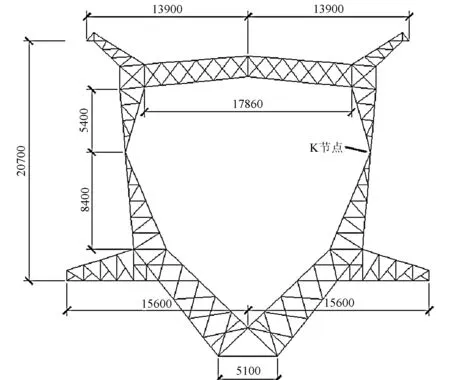
2.1 架线前统计
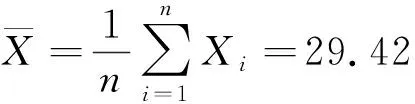
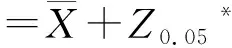
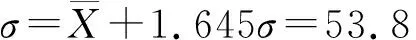



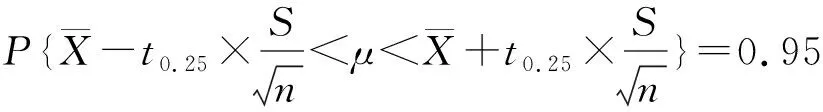
2.2 架线后统计

2.3 假设检验推断


2.4 架线前后结果分析
3 结 论

