我国省域人口发展与节约型社会建设的耦合协调发展度研究*

丁 刚，金少芸，黄志强

(福州大学 公共管理学院，福建 福州 350002)

一、引言

近年来国内外对于人口与建设节约型社会的关系研究，往往仅注重强调建设节约型社会进程中人口问题的重要性，却忽视了两者之间的内在耦合机制究竟如何。对于不同系统或运动形式之间的耦合协调发展问题，国内外已有不少学者进行了相关研究，如Haken.H曾通过对于系统自组织过程的研究，认为子系统间的相互协同(耦合)将导致宏观的空间或时间有序结构；[1]刘耀彬等曾以关联度分析为依托提出其用以测度两个系统耦合程度强弱的耦合度模型等。[2]上述研究无疑是积极和有意义的，但值得指出的是，基于耦合协调发展的视角，从人口发展与节约型社会建设的内涵入手，构建相应的评价指标体系，在对两者现状水平运用GCPA(全局主成分分析)模型进行评价的基础上，运用耦合协调发展度模型对两者间关系进行较全面系统分析的研究尚未在该领域充分展开。

本文拟从耦合协调发展的视角对于我国人口发展与节约型社会建设之间的关系进行研究，对构建统筹人与自然和谐发展的有效体制和机制，丰富和发展人口理论具有一定的现实意义。

二、 耦合协调发展度的界定及其计算方法概述

所谓耦合，意指两个或两个以上的系统或运动形式通过各种相互作用而彼此影响的现象。当系统之间或系统内部要素之间配合得当、互惠互利时，为良性耦合；反之，相互摩擦、彼此掣肘时，为恶性耦合。[3]一般认为，可以用耦合度等指标来反映两个或两个以上的系统或运动形式间的相互作用及影响程度。截至目前，国内已有不少学者就耦合度问题进行了研究，如刘耀彬等曾运用耦合度模型定量揭示出中国省区城市化与生态环境系统耦合的主要因素，并从时空角度分析了区域耦合度的空间分布及演变规律。[4]黄金川等亦曾就城市化与生态环境之间的交互耦合机制及规律性问题进行了相关阐述等等。[5]但耦合度指标显然未包含发展水平这一层面的信息，为较全面地分析城镇化建设与节约型社会建设两者之间的协调发展程度，尚需通过耦合协调发展度这一指标对其进行评价。本文所研究的耦合协调发展度，系指一个在适度考量两个或两个以上的系统或运动形式发展水平的基础上，用以全面反映其耦合作用中协调性程度高低的综合评价指标。在借鉴廖重斌等提出的协调发展度模型的基础上，本文利用如下公式对其进行计算：[6]

(1)

式中，D为耦合协调发展度，f(x)、f(y) 分别为用以反映人口发展现状与节约型社会建设现状的相关评价指数，k(≥2)为调节系数，本文取其一般值为2，α、β为待定权数，本文视人口发展和节约型社会建设同等重要，故按α=β=0.5为其赋值。

对于D，可按其取值范围做不同类型的划分。在借鉴有关研究成果后，[2]本文对其做如下界定(见表1)：

表1 耦合协调发展度的协调等级划分

三、 我国省域人口发展水平的总体现状评价

(一)评价指标体系的基本框架

在充分认识人口发展的涵义及其基本特征的基础上，参考已有研究成果，本研究拟从构成人口环境的四个有机层面：人口数量、人口质量、人口结构、人口分布入手，选择相应指标对我国省域人口发展水平进行综合评价，其基本构成包括总和生育率、人口出生率、每千人医院床位数、每千人卫生机构技术人员数、人均受教育年限、平均预期寿命、非农产业就业人员比重、人口综合经济密度、城镇人口比重、总抚养比等变量指标。

(二)评价模型——GCPA模型的建立方法介绍

在现有的各种绩效综合评价方法中，主成分分析方法是一种重要的多元统计方法，然而，在省域人口发展水平评价研究中，如果对每年的数据表分别进行主成分分析，则不同的数据表有完全不同的主超平面，因而无法保证系统分析的统一性、整体性和可比性。因此，对这种立体数据表进行主成分分析，就要寻求一个对所有数据表来说是统一的简化的空间，将每张数据表在其上的投影得以近似表示，并且从全局来看，该空间的综合效果是最佳的，这种处理方法，称为全局主成分分析，据此可建立起相应的GCPA模型。在具体处理时，可按如图1所示的基本步骤来完成这一系列过程。

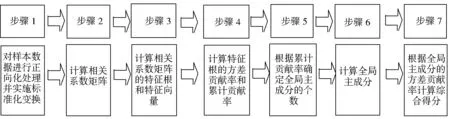
图1 GCPA模型的构建步骤

(三)评价过程简介

基于《中国统计年鉴》(2007、2008)，本文构造了一个2006、2007年全国各个省市的相关数据(由于数据获取的原因，这里不包括西藏自治区)，并将所获得的10项指标构成的数据按照时间顺序依次排列，制成全局样本数据表。运用多元统计分析软件SPSS16.0，对样本数据进行了正向化处理，并实施了标准化变换后所进行的KMO和Bartlett球形假设。检验结果表明，检验变量间偏相关性的KMO统计量数值为0.858，球形假设检验的结果显著性水平为0.000，可见对样本数据进行全局主成分分析是合适的。

通过进行全局主成分分析，可得到全局主成分的特征值及贡献率，结果表明，F1、F2(分别代表第一、二个全局主成分)两个全局主成分的方差累计贡献率已达83.719%(大于80%)，其各自的方差贡献率分别为75.806%、7.913%，故可将其确定为所需要提取的两个全局主成分，由此可写出综合得分的评价公式如下：

F综=0.758 06F1+0.07913F2.

(2)

经运算所实际得到的全局主成分矩阵如表2所示，由此表中所示列向量、特征值和标准化后的指标值可以写出各全局主成分的计算公式，如式(3)-(4)所示。

F1=0.268 278 5Z1+0.328 306 4Z2+0.303 685 9Z3+0.322 940 5Z4+0.339 249Z5+0.301 708 3Z6+0.317 365 2Z7+0.312 310 9Z8+0.316 334 9Z9+0.345 491 9Z10.

(3)

F2=0.268 278 5Z1+0.328 306 4Z2+0.303 685 9Z3+0.322 940 5Z4+0.339 249Z5+0.301 708 3Z6+0.317 365 2Z7+0.312 310 9Z8+0.316 334 9Z9+0.345 491 9Z10.

(4)

其中，F1、F2表示各全局主成分，Zi表示指标i经标准化后的指标值，共有10项指标，i=1，2，…，10。利用以上公式及综合得分的评价公式，可计算出全国各省(市)区的全局主成分值及综合结果F综。

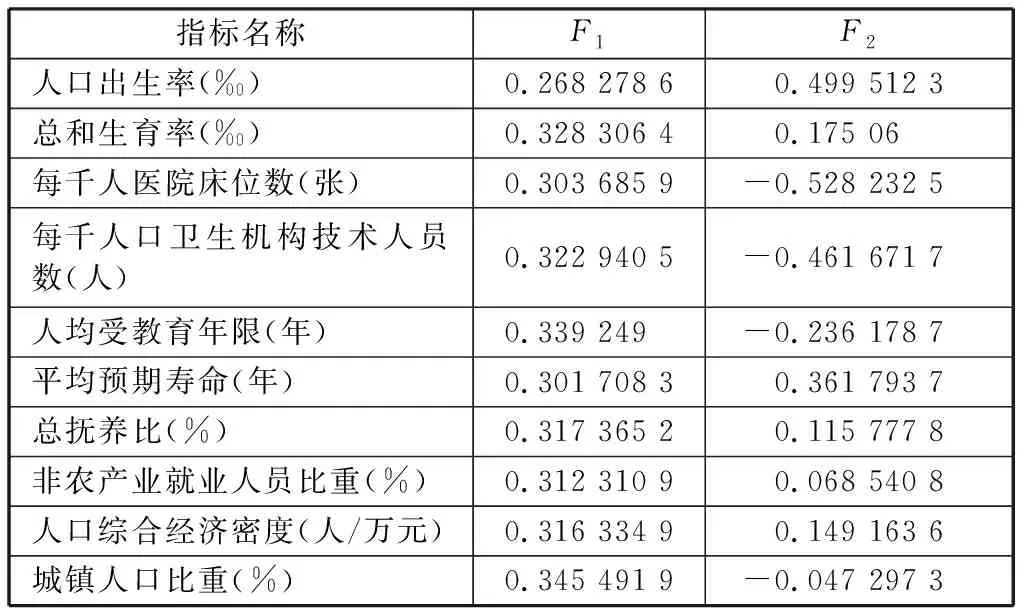
表2 所实际得到的全局主成分矩阵

计算结果表明，同2006年相比，2007年我国东、中、西三大地带各省(市)区的F综均有不同程度的上升，这意味着其人口发展水平都有了一定程度的改善。而从各省(市)区在全国范围内的排名状况来看，2006-2007年排名上升的省(市)区共有3个，分别为江苏、湖北、江西，主要在东部和中部地区；排名下降的省(市)区共有4个，分别为福建、黑龙江、安徽和山西，大多数属于中部地区；其余省(市)区的排名保持不变。通过进一步计算可知，同2006年相比，2007年东部、中部和西部地区的平均综合得分的上升幅度分别为0.021 905 、0.072 932 和0.118 966，西部最高，中部次之，东部最低，使得全国范围内各地区人口发展水平之间的发展差距趋于缩小。2006至2007年，各省(市)区综合得分的极差由9.579 063降至9.145 588，亦反映了这一发展趋势。

基于上述评价结果，本研究以2007年各省(市)区的综合得分F综为依据，以欧氏距离平方(Squared Euclidean distance)衡量单位间距离，对其进行Q型聚类，其结果表明：

1.北京、上海人口发展现状水平最好，属于第一类地区；

2.天津、辽宁、吉林、黑龙江、浙江、江苏、广东等7个省(市)区的人口发展现状水平较好，属于第二类地区；

3.内蒙古、河北、山西、福建、山东、河南、湖南、湖北、海南、四川、重庆、陕西、宁夏、新疆等14个省(市)区的人口发展现状水平较为一般，属于第三类地区；

4.安徽、江西、云南、青海、甘肃、广西、贵州等7个省(市)区的人口发展现状水平较差，属于第四类地区，且该类省(市)区多属于中、西地区。

四、 我国省域节约型社会建设水平的总体现状评价

(一)评价指标体系的基本框架

在充分认识节约型社会的涵义及其基本特征的基础上，借鉴已有的节约型社会指标体系的研究成果，本文拟从节能、节水、节地和资源综合利用等四个操作性较强的层面构建评价指标体系。其中，节能层面选取了三个具代表性的指标：单位地区生产总值能耗、单位地区生产总值电耗、单位工业增加值能耗；节水层面选取了两个具代表性的指标：人均用水量、万元GDP用水量；节地层面囿于数据的可得性仅选取了一个具代表性的指标：万元GDP建设用地面积；资源综合利用层面的相关指标则分别从固体废弃物、废水、废气及生活垃圾处理等四个方面选取，主要包括：工业固体废物综合利用率、工业废水排放达标率、工业SO2排放达标率和生活垃圾无害化处理率。

(二)评价过程简介

基于《中国统计年鉴》(2007、2008)及《中国国家统计局专题统计数据之环境统计数据》中相关统计数据(不包括西藏自治区)，可将所获10项指标构成的数据表按时间顺序依次排列，制成全局样本数据表。运用多元统计分析软件SPSS，对样本数据进行了正向化处理，并实施了标准化变换后所进行的KMO和Bartlett球形假设检验。结果表明，检验变量间偏相关性的KMO统计量数值为0.747，球形假设检验的结果显著性水平为0.000，对样本数据进行全局主成分分析是合适的。

进行全局主成分分析，可得到全局主成分的特征值及其贡献率，如表3所示。可见，前4个全局主成分的方差累积贡献率已达85.18%(高于85%)，其中、F1、F2、F3、F4(分别代表第一至第四个全局主成分)的方差贡献率分别为53.68%、13.52%、9.20%、8.78%，故可将其确定为所需提取的四个全局主成分，由此可写出综合得分F综的评价公式：

F综=0.536 8F1+0.135 2F2+0.092F3+0.087 8F4.

(5)

经运算所实际得到的全局主成分矩阵如表3所示，由此表中所示列向量、特征值和标准化后的指标值可以写出各全局主成分的计算公式，如式(6)-(9)所示。其中，F1、F2、F3、F4表示各全局主成分，ZXi表示指标Xi经标准化后的指标值，共有10项指标，i=1,2,…，10。利用以上公式及综合得分的评价公式，可计算出全国各省(市)区的全局主成分值及综合结果F综。

(6)

(7)

(8)

(9)

表3 所实际得到的全局主成分矩阵

计算结果表明，同2006年相比，2007年我国东、中、西三大地带各省(市)区的F综都有不同程度的上升。2006-2007年排名上升的省(市)区共有6个，多半属于西部地区；排名下降的省(市)区共有9个，绝大多数属于东部地区和中部地区；其余省(市)区的排名保持不变。同2006年相比，2007年东部、中部和西部地区的平均综合得分的上升幅度分别为0.163 、0.333 和0.426，西部最高，中部次之，东部最低，使得全国范围内各地区节约型社会建设水平之间的发展差距趋于缩小。2006-2007年，各省(市)区综合得分F综的极差由4.556降至4.344，亦反映了这一发展趋势。

基于上述评价结果，本研究运用分层聚类分析法(Hierarchical Cluster)，以2007年各省(市)区的综合得分F综为依据，对其进行Q型聚类，聚类结果表明：

1.北京、天津、浙江、福建、江苏、山东、上海、广东等8个东部省(市)区节约型社会建设现状水平相对较好，属于第一类地区；

2.四川、重庆、江西、辽宁、湖南、广西、河北、湖北、安徽、河南、陕西等11个省(市)区的节约型社会建设现状水平较为一般，属于第二类地区；

3.海南、吉林、云南、黑龙江等4个省(市)区的节约型社会建设现状水平较差，属于第三类地区；

4.山西、贵州、内蒙古、甘肃、宁夏、青海、新疆等7个省(市)区的节约型社会建设现状水平最不理想，属于第四类地区，且该类省(市)区多属于西部地区。

五、 我国人口发展与节约型社会建设之间的耦合协调发展度测度结果

(一)耦合协调发展度的计算结果

在确知我国省域人口发展水平与节约型社会建设水平后，可按公式(1)对两者间的耦合协调发展度进行计算和测度，具体结果如表4所示。同2006年相比，2007年我国东、中、西三大地带各省(市)区的耦合协调发展度都有不同程度的上升，意味着其人口发展与节约型社会建设之间的协调发展状况有了一定程度的改善。从各省(市)区在全国范围内的排名状况来看，2006-2007年排名上升的省(市)区共有5个，分别为宁夏、青海、湖北、江西、山西，主要属于西部地区(所占比例为2/5)和中部地区(所占比例为3/5)；排名下降的省(市)区共有8个，分别为新疆、云南、贵州、广西、福建、海南、湖南、河南，其中属于西部地区所占比例为4/8、东部地区所占比例为2/8、中部地区所占比例为2/8；其余省(市)区的排名保持不变。由此可见，动态而言，西部地区人口发展与节约型社会建设之间的耦合协调发展度的提升相对于中、东部地区而言更为明显。通过表4中数据经进一步计算可知，同2006年相比，2007年东部、中部和西部地区的平均综合得分的上升幅度分别为0.015 332、0.062 283 和0.327 902，西部最高，中部次之，东部最低，使得全国范围内各地区之间的耦合协调发展度差距趋于缩小。2006-2007年，各省(市)区耦合协调发展度得分的极差由0.996 013降至0.814 576，亦反映了这一发展趋势。

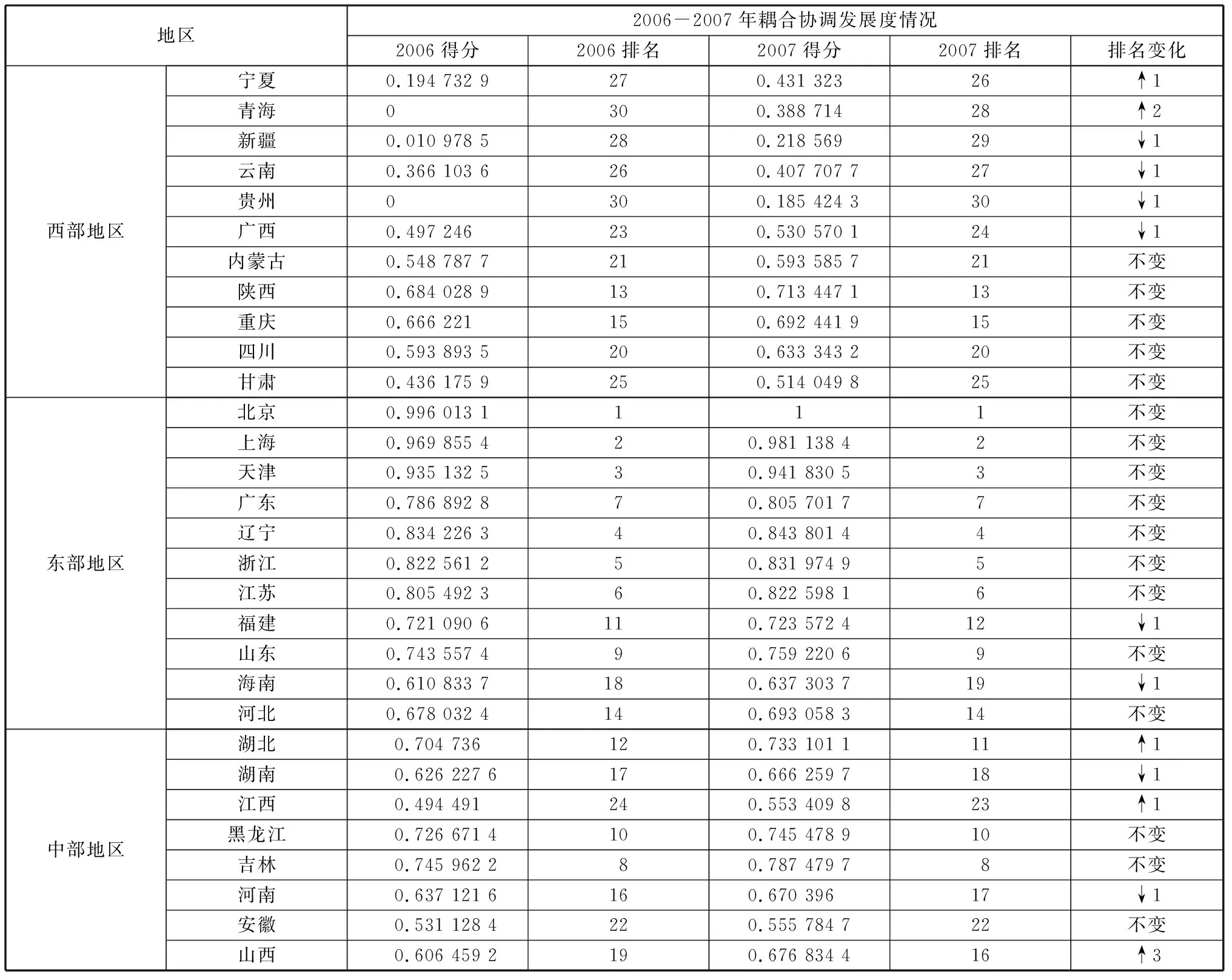
表4 评价结果概览

为对各地区耦合协调发展度的不均衡状况进行详细解读，本研究拟通过对统计学意义上的离散系数(Coefficient of Variance)的计算，利用公式(10)来反映其不均衡程度及变化情形。

CV=δ/μ.

(10)

其中CV代表离散系数，δ为标准差，μ为平均值。计算结果如图2所示，计算结果表明，就区域内部的耦合协调发展度不均衡状况而言，东部地区最小，中部地区最大，西部地区最高。2006-2007年，三大地区这一不均衡状况均有所改善。

图2 我国各地区耦合协调发展度离散系数的计算结果

(二)基于计算结果的省域协调等级划分

为了更直观地了解全国范围内省域协调等级的划分情况，可对2007年各省按其耦合协调发展度得分由表1所示等级标准进行划分，结果表明：

1.北京、上海、天津、广东、辽宁、浙江、江苏等7个地区属于优质协调(VII型)，即人口发展与节约型社会建设水平耦合协调发展最好的省市，且都属于东部地区；

2.陕西、福建、山东、湖北、黑龙江、吉林等6个地区属于中度协调(VI型)，即人口发展与节约型社会建设水平耦合协调发展较好的地区；

3.重庆、四川、海南、河北、湖南、河南、山西等7个地区属于轻度协调(V型)，即人口发展与节约型社会建设水平耦合协调发展一般的地区；

4.安徽、江西、甘肃、内蒙古、广西等5个地区属于勉强协调(IV型)，即人口发展与节约型社会建设水平耦合协调发展勉强合格的地区；

5.宁夏、云南等2个地区属于轻度失调(III型)，即人口发展与节约型社会建设水平耦合协调发展偏差的地区，这些地区都属于西部地区；

6.青海地区属于中度失调(II型)，即人口发展与节约型社会建设水平耦合协调发展较差地区，亦属于西部地区；

7.新疆、贵州地区属于严重失调(I型)，即人口发展与节约型社会建设水平耦合协调发展最差地区，上述地区亦属于西部地区。

从分析结果来看，我国各地区人口发展与节约型社会建设间的耦合协调发展度存在显著差异，不均衡态势十分突出。在现阶段促进各地区人口与节约型社会建设协调发展的实际工作中，应因地制宜，根据不同地区的现状水平及各自特点制定相应的应对方案。从全国范围来看，考虑到新疆、贵州属于严重失调型，青海属于中度失调型，应将这些地区作为当前工作中的重中之重来区别对待。当然，对于其余地区，即便是北京、上海、天津、广东、辽宁、浙江、江苏等现状水平较为良好的地区，亦不能放松警惕，应针对其所存在的缺陷和不足有的放矢，积极应对，以防止其所取得的已有成就在未来一段时期出现退化。总之，不仅要进一步巩固和强化先进地区的转变进程，更要对其他绩效不甚理想的地区加强重视，以期达到共同推进和谐发展的良好愿景。

参考文献：

[1] 哈肯(Haken，H.).协同学导论[Z].张纪岳，郭治安，译.西安：西北大学科研处，1981.1-9.

[2] 刘耀彬，李仁东，张守忠.城市化与生态环境协调标准及其评价模型研究[J].中国软科学，2005，(5)：140-148.

[3] 吴文恒，牛叔文.甘肃省人口与资源环境耦合的演进分析[J].中国人口科学，2006，(2)：81-86.

[4] 刘耀彬，李仁东，宋学锋.中国区域城市化与生态环境藕合的关联分析[J].地理学报，2005，60(2)：237-247.

[5] 黄金川，方创琳.城市化与生态环境交互耦合机制与规律性分析[J].地理研究，2003，22(2)：211-220.

[6] 廖重斌.环境与经济协调发展的定量评判及其分类体系[J].热带地理，1999，(2)：171-177.