利用Mathematic进行的一个镜像法问题的数值模拟
付长宝,张 巍,姜丽丽,李恩奎
(通化师范学院 物理系, 吉林 通化134002)
静电学的基本问题是求解在所有边界上满足边值关系和边界条件的泊松方程的解.一种重要的特殊情形是区域内只有一个或几个点电荷,区域边界是导体或介质界面,对于这样的区域电场的求解可以采用一种特殊的方法——镜像法.镜像法求解电场的关键在于根据感应电荷与点电荷激发的场在边界上所满足的边值关系和边界条件,确定像电荷的位置和电荷量.一般情况下,利用镜像法所求得的物理问题的数学表达式是比较繁杂的,不利于对问题的物理认识.本文针对镜像法求解物理问题的这一特点,利用Mathematic,对镜像法求解静电场问题所给出的复杂数学形式进行数值模拟,并绘制相应的直观图形,进而从复杂的数学结果中提炼直观的物理认识.

图2 求球外任意一点p的电势
1 回顾运用镜像法[1-3]求解空间某点电势
若存在这样一个求解静电场的问题:真空中一半径为R0的导体球,距球心为a(a>R0)处有一点电荷Q,导体球不接地而带电荷Q0,求球外电势,并求电荷Q所受的力.
假设导体球接地时,点电荷Q及Q在球上所引起的感应电荷,在球面上所激发的静电场电势为零.若设此时点电荷Q在球内的镜像电荷为Q',考虑球面上任一点P如图1所示,边界条件要求:
Qr+Q'r'=0
(1)
式中r为Q到p的距离,r'为Q'到p的距离.因此对球面上任一点,应有:
r'r=-Q'Q=常数
(2)
由图1可看出若选Q'的位置使ΔOQ'P∽ΔOQP,则方程(2)得以满足,且有:
r'r=R0a=常数
(3)
设Q'距球心距离为b,两三角形相似的条件为bR0=R0a,即:
b=R20a
(4)
由(2)式和(3)式得
Q'=-R0aQ
(5)
(4)式和(5)式给出了假想电荷Q'的位置和大小.
方程(4)和(5)给出的是假设导体接地时,点电荷Q在导体球内部的镜像电荷的位置和大小.但问题当中,导体球并没有接地且导体球所带有的电荷量为Q0,那么点电荷Q与导体球所带有的电荷Q0,以及导体上产生的感应电荷在导体球面上所激发的电势应为大于零的常数.这时,所求解的问题的边界条件为:导体球所带的总电荷量为Q0,同时球面为等势面.根据边界条件要求,若在假想导体球接地的基础上,再在球心处放置一假想电荷Q0-Q'此时原问题的所有边界条件得以满足,球外任一点p的电势如图2所示为:
ψ(p)=14πε0(Qr-R0Qar'+Q0+(R0Qa)R)
(6)
其中1r=1R2+a2-2Racosθ,
1r'=1R2+b2-2Rbcosθ
ψ(R,θ)=14πε0[QR2+a2-2Racosθ-
R0Qa1R2+b2-2Rbcosθ+Q0+R0Q/aR]
(7)
电荷Q所受到的静电场力为:
4πε0F=Q(Q0-Q')a2+QQ'(a-b)2=
QQ0a2-Q2R30(2a2-R20)a3(a2-R20)2
(8)
由方程(7)和方程(8)可知,利用镜像法求解静电场问题时,得到的结果在数学形式上比较复杂,由直接的计算结果出发不利于对问题的物理认识.如直接的观察方程(7)很难判断Ψ随R和θ的变化关系,同样从方程(8)出发也很难直接判断出当a发生变化时F随a的变化关系.
2 利用Mathematic[4]数值模拟绘制图形
Mathematic是一款较著名的数学工具软件,其功能强大,可实现符号运算、绘制图形、程序设计等功能,近年来被广泛的应用到科技论文的写作中.下文将利用Mathematic对方程(7)、(8)进行数值模拟绘制图形.
根据方程(7)在取参数R0=2,b=1,a=3,Q=5,Q0=2.5,且R∈(2,100),θ∈(0.01,0.99π)时绘制函数ψ(R,θ)随半径和极角变化的图形如图3:
由图3可十分容易得知Ψ随半径R和极角θ的变化关系:当极角θ一定时,Ψ随R的增大而减小;当半径R一定时,Ψ随θ的增大而减小.
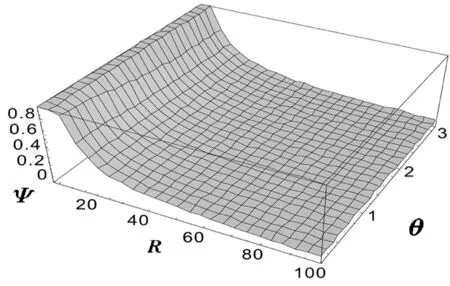
图3 Ψ随R和θ的变化关系图
根据方程(8)在取参数Q=5,Q0=2.5,R0=2,同时有a∈(3,60)时绘制函数F(a)随a的变化关系图如图4.

图4 F随a的变化关系图
由图4可知,在a∈(0,4)的范围内,点电荷Q所受到的静电场力为导体球上所带有的自由电荷Q0与导体上的感应电荷对它的作用力的合力,效果上表现为引力,且引力随着a的增大而逐渐减小;当a=4时,点电荷Q所受到的静电场力合力为零;当a∈(4,60)时点电荷Q所受到的静电场力合力表现为斥力,初始时斥力随a的增大而增大,当a=6时斥力取得最大值,然而在a∈(6,60)的范围内斥力将随a的增大而减小并无限接近于零.
综上所述,本文针对镜像法求解问题中所给出的问题的结果过于复杂,不利于对问题的物理上的认识这一特点,利用Mathematic对镜像法求解问题中所给出的数学结果进行了数值模拟,并绘制了相应的直观图形,发现由直观的曲线图形出发十分方便提炼复杂数学结果中包含的物理规律.
参考文献:
[1]郭硕鸿.电动力学[M].人民教育出版社,1997.
[2]蔡圣善,等.电动力学[M].高等教育出版社,2002.
[3]陈世民.电动力学简明教程[M].高等教育出版社,2004.
[4]丁大正.Mathematic4教程[M].电子工业出版社,2002.

