子母弹最佳抛撒半径与导弹精度关系研究

谭守林,张金巍,陈 力

(第二炮兵工程学院603教研室,陕西西安,710025)

现代战争中,利用导弹子母弹封锁敌机场跑道是夺取制空权的重要手段。子母弹抛撒半径不同,子弹分布密度和爆炸效应就不同,对目标的毁伤效果也不同。子母弹抛撒半径可以通过改变抛撒高度和侧向抛撒速度来调整。在目标、武器数量和性能等条件相同的情况下,通过对子母弹抛撒半径的优化选择,可以使子母弹对目标的打击效果达到最佳。

不同型号的导弹,其精度往往不同,在制定火力计划时需要考虑导弹精度对打击效果的影响。本文在分别研究了导弹精度和子母弹抛撒半径对打击效果的影响后,运用优化算法求出子母弹最佳抛撒半径。为了更好地研究子母弹最佳抛撒半径随导弹精度的变化规律,本文拟合出二者的函数关系式,以期为子母弹弹头设计和火力应用提供参考。

1 基于Monte Carlo的机场跑道失效率计算模型

1.1 瞄准点的选择

机场跑道是一类典型的窄长形面目标,一般情况下,跑道长L为3 000 m,宽B为46 m,长宽比达65∶1。导弹子母弹的抛撒半径一般为100～400 m,其抛撒圆环直径远远大于跑道宽度,故可假设跑道为均匀线目标。在研究导弹子母弹打击机场跑道目标时,瞄准点的选取按均匀选点的原则进行[1],即瞄准点以目标中心为基点、沿跑道长度方向对称等间隔分布,间距dx=L/M,其中M为发射导弹数。

取原点o′为机场跑道中心点,x′轴过原点与跑道方向平行,y′轴在跑道平面内过原点垂直于x′轴,构造目标坐标系x′o′y′。

设第i枚导弹(i=0,1,…,M-1)的瞄准点为(xi,yi),则

1.2 子弹落点散布模拟

1.2.1 母弹随机落点模型[2]

设导弹的圆概率偏差为CEP,母弹落点(mx,my)服从(μ1,μ2,σ1,σ2,ρ)二维正态分布,其中:μ1、μ2分别为母弹落点坐标的均值,即μ1=xi,μ2=yi;σ1、σ2为导弹的射击精度,σ1=σ2=σ;ρ为x方向与y方向的相关系数,若坐标轴与主散布轴平行,则射向与侧向散布互相独立,即相关系数ρ=0。射击精度与CEP的关系为

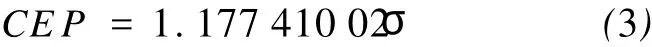
第i枚母弹落点坐标为

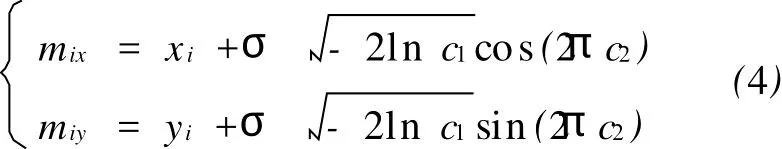
式中:xi、yi为第i枚导弹的瞄准点坐标;c1、c2为(0,1)区间上相互独立的均匀分布随机数。

1.2.2 子弹随机落点模型[3]

以子弹的抛撒中心为原点o,建立子弹落点坐标系xoy,子弹落点分布在以母弹落点为圆心的圆环内,圆环外径为子弹抛撒半径R,内径为盲区半径r,取r/R=0.3。假设子弹在圆环中服从径向均匀分布,第i枚母弹第j个子弹的落点坐标为(xij,yij),则有

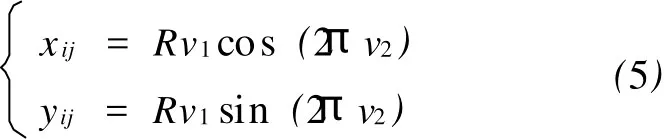
式中:v1为(r/R,1)区间上均匀分布随机数;v2为(0,1)区间上均匀分布随机数,且与v1相互独立。

为便于计算对目标的毁伤效果,通常把子弹落点坐标转换到目标坐标系。子弹落点在目标坐标系中的坐标为

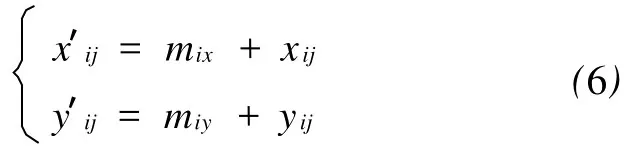
1.3 机场跑道失效率的计算

对于机场跑道这类窄长形目标,主要采用跑道失效率作为其毁伤指标,下面给出跑道失效率的计算步骤。

(1)判断子弹落点是否在跑道上。设弹坑半径为r0,如果r0且则子弹落点在跑道上,记为(x(k),y(k)),k=1,2,…,S,其中S为落在跑道上的子弹个数。

(2)判断是否存在最小升降窗口。

最小升降窗口是指飞机在跑道上安全起飞或降落所需的最小完好矩形区域,设其长度为WL,宽度为WB。

对于整条跑道,边界条件取为

将子弹落点(x(k),y(k))按x(k)的增序排列,即x(0)≤x(1)≤…≤x(S)≤x(S+1)。如果存在x(k)-x(k-1)≥WL(k=1,2,…,S+1),则封锁失败,停止搜索;否则,以x向坐标最小的子弹落地(x(0),y(0))为起点,在跑道上以最小升降窗口长度WL为定步长,得到一个区间,搜索其中的弹着点,对各弹着点的y向坐标进行排序,判断是否存在相邻两点的y向间距大于最小升降窗口宽度WB,如果存在,则封锁失败,停止搜索;否则,依次以子弹落点(x(k),y(k))(k=1,2,…,S+1)为起点,重复上一步操作,其中,如x(k)与x(S+1)的x向间距小于WL,则跑道失效,停止搜索,否则继续搜索,直到确认跑道上没有最小升降窗口或者封锁失败。

(3)计算跑道失效率。

采用Monte Carlo模拟方法计算跑道失效率。设总的模拟次数为N,其中跑道失效的次数为N1,则跑道失效率P为

经过多次仿真实验表明,当N取5 000时,跑道失效率的计算结果较为准确。

2 导弹精度和子母弹抛撒半径对机场跑道失效率的影响

导弹精度是评定子母弹对目标毁伤效果的重要条件。导弹精度包括导弹落点的准确度和密集度。准确度描述落点散布中心离开目标的距离,是一个系统值,常以落点纵向和横向的系统偏差来表示。密集度描述随机落点围绕散布中心的分布状况,反映了落点随机性误差的大小,以导弹纵向和横向落点的方差来表示。当导弹纵、横向落点的方差相同时,落点分布称为圆散布,此时常以导弹落点的圆概率偏差CEP表示落点随机性误差[4]。本文不考虑导弹系统误差,即认为落点散布中心与目标点重合,导弹落点随机误差采用圆概率偏差CEP,因此以下导弹精度均指CEP。

子母弹抛撒半径是影响导弹子母弹对目标毁伤效果的另一重要指标,也是弹道设计和计算诸元要考虑的重要因素。

下面通过仿真计算来研究导弹精度及子母弹抛撒半径对跑道失效率的影响。设跑道长L=3 000 m,跑道宽B=46 m,最小升降窗口长WL=800 m,最小升降窗口宽WB=20 m,弹坑半径r0=1 m;导弹数量为5枚,子弹个数为70,导弹精度CEP从50 m变化到200 m,子母弹抛撒半径从50 m变化到500 m。用VC++6.0编程并用M atlab软件绘图,得出跑道失效率与导弹精度、子母弹抛撒半径的关系如图1所示。

从图1中可以看出:①在其他条件相同时,跑道失效率随着CEP的增大迅速降低,但随着子母弹抛撒半径的增加,CEP对跑道失效率的影响逐渐减弱;②在其他条件相同时,随着子母弹抛撒半径的增大,跑道失效率呈先增大后减小的变化趋势,即存在一个子母弹最佳抛撒半径使跑道失效率达到最大。

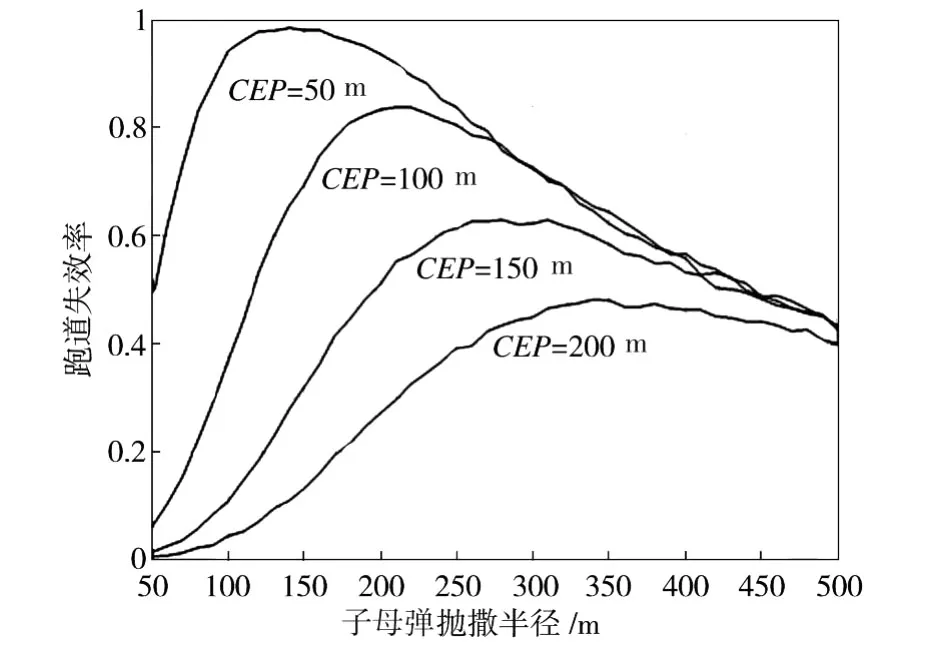
图1 不同导弹精度及子母弹抛撒半径下的跑道失效率Fig.1 DPR at differentm issile’s precisionsand separation radius

3 子母弹最佳抛撒半径的计算

从图1可以看出,跑道失效率是CEP的单峰函数,峰值顶点对应的抛撒半径即为子母弹最佳抛撒半径,随着CEP的增加,子母弹最佳抛撒半径也在增加。利用优化算法可以求出每一个CEP对应的最佳抛撒半径。

下面运用黄金分割法[5]求出不同导弹精度下的子母弹最佳抛撒半径。在本文中可假设φ(α)为子母弹抛撒半径为α时通过Monte Carlo模拟计算的跑道失效率。令a1、b1为子母弹抛撒半径的下限和上限,则φ(α)为搜索区间[a1,b1]上的单峰函数。设在第k次迭代时搜索区间为[ak,bk],取两个试探点λk、μk∈[ak,bk],且λk<μk,并满足下列条件:①λk和μk到搜索区间[ak,bk]的端点等距;②每次迭代时,搜索区间长度缩短率相同。然后比较φ(λk)和φ(μk)的大小,并逐步缩小搜索区间。具体步骤如下:

(1)选取初始数据。确定搜索区间[a1,b1]和精度要求δ,按式(9)和式(10)选取最初两个试探点λ1和μ1。

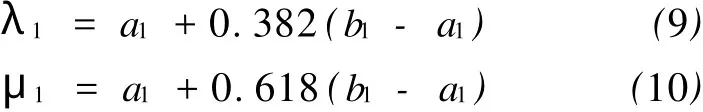
计算φ(λ1)和φ(μ1),令k=1。

(2)比较函数值。若φ(λk)>φ(μk),转步骤(3);若φ(λk)≤φ(μk),则转步骤(4).

(3)若bk-λk≤δ,则停止计算,输出μk;否则,令ak+1=λk,bk+1=bk,λk+1=μk,φ(λk+1)=φ(μk),μk+1=ak+1+0.618(bk+1-ak+1)。计算φ(μk+1),转步骤(5)。

(4)若μk-ak≤δ,则停止计算,输出λk;否则,令ak+1=ak,bk+1=μk,μk+1=λk,φ(μk+1)=φ(λk),λk+1=ak+1+0.328(bk+1-ak+1)。计算φ(λk+1),转步骤(5)。

(5)令k=k+1,转步骤(2)。

4 子母弹最佳抛撒半径与导弹精度的函数关系拟合

为了确定CEP与子母弹最佳抛撒半径的关系,本文在用5枚子母弹打击机场跑道的情况下,求出不同CEP对应的最佳抛撒半径,采用最小二乘函数拟合法分别拟合出子母弹最佳抛撒半径与CEP的一次、二次和三次函数关系式。

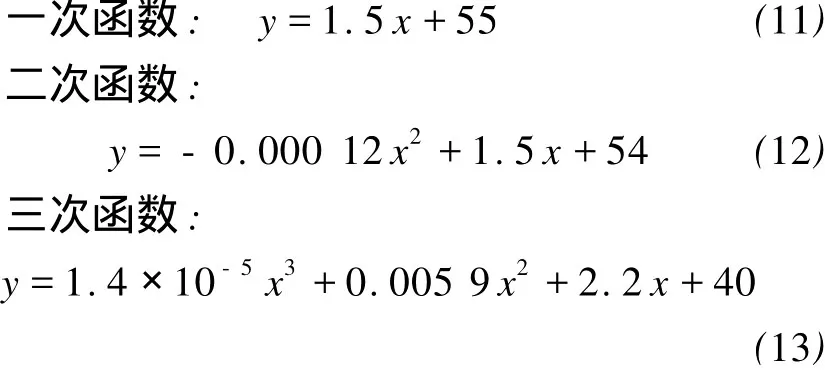
式中:x为导弹精度CEP;y为子母弹最佳抛撒半径。图2为各次函数的拟合曲线,其中,一次函数和二次函数的拟合曲线几乎重合。

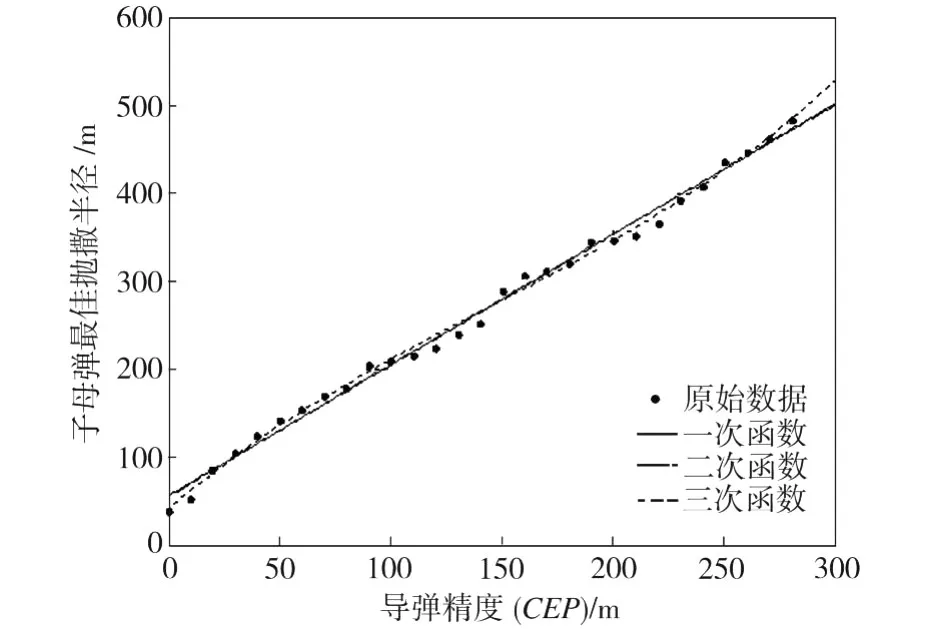
图2 子母弹最佳抛撒半径与导弹精度的关系Fig.2 Relationship between submunition missile’s best separation radius and precision

从式(12)～式(13)可以看出,二次函数和三次函数中高次项的系数都比较小,接近于零,因此可以忽略其高次项。从图2中也可以看出,二次函数和三次函数拟合曲线比较接近于直线。为了计算方便,可以认为子母弹最佳抛撒半径与导弹精度的关系为线性关系,即用5枚子母弹打击机场跑道时,二者的函数关系为y=1.5x+55。同样,可以拟合出用6枚或7枚子母弹打击目标的情况下子母弹最佳抛撒半径与导弹精度的函数关系。

5 结语

本文基于机场跑道失效率计算模型,利用Monte Carlo模拟方法研究了导弹精度和子母弹抛撒半径对机场毁伤效果的影响,并利用黄金分割法求出子母弹最佳抛撒半径,最后运用最小二乘法拟合出子母弹最佳抛撒半径与导弹精度的函数关系式,通过比较得出二者近似为线性关系。本研究可以为子母弹的火力应用和诸元快速计算提供参考。

[1] 邱成龙.地地导弹火力运用原理[M].北京:国防工业出版社,2001:113-115.

[2] 雷宁利,唐雪梅.侵彻子母弹对机场跑道的封锁概率研究[J].系统仿真学报,2004,16(9):2 030-2 032.

[3] 舒健生,李亚雄,苏国华.子母弹抛撒盲区对毁伤效果的影响研究[J].弹箭与制导学报,2008,28(3):150-152.

[4] 张金槐.远程火箭精度分析与评估[M].长沙:国防科技大学出版社,1995:1-3.

[5] 袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,2005:69-73.