Huffman编解码及其快速算法研究

李晓飞

摘 要:Huffman压缩编码是一种较好的变长前缀码,它由D.A.Huffman于1952年发明。Huffman编码作为一种高效而简单的可变长编码而被广泛应用于信源编码等方面。介绍了基本的Huffman编码算法,并针对其缺点,提出了动态Huffman编码算法,改进算法对数据进行编码的依据是动态变化的Huffman树。

关键词:Huffman编码;数据压缩;Huffman树;优化算法

中图分类号:TN911 文献标识码:A

文章编号:1004-373X(2009)21-102-03

Huffman Codec and Its Fast Algorithm

LI Xiaofei

(Shaanxi Railway Institute,Weinan,714000,China)

Abstract:Huffman coding is a good variable-length prefix code,invented by D.A.Huffman in 1952.Huffman coding as an efficient and simple variable-length coding has been widely used in areas such as source coding.The basic Huffman coding algorithm is introduced,and for its shortcomings,dynamic Huffman coding algorithm is introduced,improved algorithm to encode the data is based on dynamic changes of the Huffman tree.

Keywords:Huffman coding;data compression;Huffman tree;optimization algorithm

0 引 言

随着科技与经济的迅速发展,海量的数据进入了人们的生活。20年前,以兆字节为单位的存储要求也是异想天开的事情。可是现在,随着大容量存储设备的迅速发展,即使对于个人用户来说,存储上千兆字节的数据也很平常,并且离太字节的存储量也不再遥远。如何正确而迅速的处理和保存这些数据就成为计算机科学中亟待解决的一大问题。因此,数据压缩技术已经成为计算机科学的主要分支。所谓数据压缩,实际上就是对需要压缩的数据对象进行某种可逆性编码,使编码的总长度小于原数据的总长度,从而达到减小数据总长度的目的。数据压缩的关键在于编码,编码就是基于由模型提供的概率分布来确定符号的输出表达方式。对于以数据压缩为目的的编码,一般的想法是对于常见的符号,编码器输出较短的码字;而对于少见的符号则用较长的码字表示[1]。

自1952年提出Huffman编码以来,在过去的50年中,Huffman算法一直得到国内外相关领域学者的关注,并取得了许多重要的进展。随着信息技术的发展,Huffman编码作为高效的无损压缩的重要方法正日益广泛地在文本、图像、视频压缩及通信、密码等领域得到应用。

1 静态Huffman编码

1.1 Huffman编码的原理

Huffman编码是一种变长度编码方法,只要给定符号的概率分布,Huffman编码算法就能够计算出给定字符的代码。对于给定概率分布的无前缀代码,产生的码字可实现很好的压缩效果。Huffman编码通过从底向顶构造解码树来解码。其编码算法为每一个符号创造一个包含了这个符号和概率值的叶结点(见图1),然后把具有最小概率值的两个叶结点排列在同一个父结点下,成为兄弟结点,父结点的概率值等于两个子结点的概率值之和(见图2)。

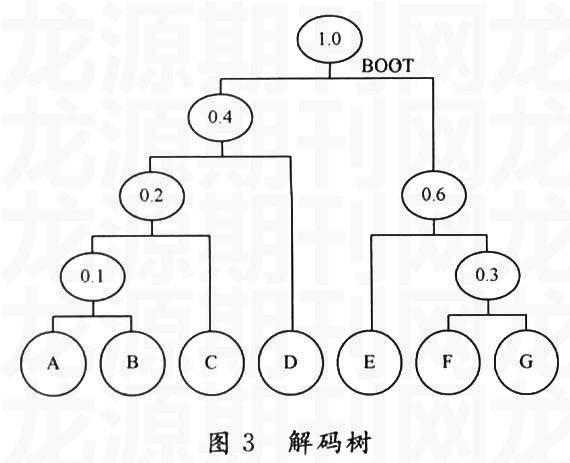
忽略已连接的子结点,选择两个具有最小概率值的子结点重复进行连接操作。例如,A与B已连接生成新的结点,下一步就是要把这个新的结点与结点C连接起来,产生一个概率为P=0.20的结点。将这个过程重复下去,直到只有一个结点没有父结点为止,这个结点即成为解码树的根(见图3)。那么,两个没有叶结点的分支就被标记为0和1(顺序并不重要)从而形成树。

生成Huffman树的具体步骤如下:

(1) 根据给定的n个权值为W1,W2,…,Wj 构成n棵二叉树的集合F={T1,T2,…,Tn),其中每棵二叉树T1中只有一个带权为Wi的根结点,其左右子树均空。

(2) 在结点集中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的结点的权值为其左、右子树上结点的权值之和。

(3) 在结点集中删除这两棵树,同时将新得到的二叉树加入结点集中。

(4) 重复步骤(2)和(3),直到结点集中只含一棵树为止,这棵树便是Huffman树。

生成Huffman树之后,在树的左右分枝上赋值1和0即可得到Huffman编码。

由于Huffman树中没有度为1的结点,一棵有n个叶子结点的Huffman树共有2n-1个结点,可以以一个大小为2n-1的向量表示。由于在构成Huffman树之后,为求得编码,需从叶子结点出发走一条从叶到根的路径;而为译码需从根出发走一条从根到叶子的路径。则对每个结点而言,既需知道其双亲的信息,又需知道其子结点的信息。

译码的过程是,分解原文中字符串,从根结点出发,按字符‘0或‘1确定访问子结点的路径,直至叶结点,便求得该子串相对应的字符。

在Huffman编码过程中,当出现2个以上最小概率的结点时,若选择树中叶结点概率为最小者与叶结点概率为最大者进行合并,则得到相应编码的平均偏离方差为最小(注:定理的逆定理不真)。上述的Huffman编码是利用压缩对象出现频率的不等性进行编码的一种常用的无损数据压缩方法。不论从算法的复杂度还是在实现的难度以及对数据压缩的效果来看,Huffman编码都不失为一种较好的数据压缩算法。

1.2 静态Huffman编码压缩算法的程序实现

以下步骤是实现的静态Huffman编码的压缩和解压缩算法。

(1) 扫描原文件的全部数据,完成字符出现概率的统计。

(2) 依据字符概率建立Huffman树。

(3) 将Huffman树的信息写入输出文件(压缩后文件),以备解压缩时使用。

(4) 进行第二遍扫描,将原文件所有字符转化为Huffman编码,并以ASCII字符形式保存到输出文件。

(5) 在输出文件上做标记以标识压缩文件,完成对原文件的压缩。

该程序的算法源于静态Huffman编码的经典思想。即压缩时,首先扫描原文件的全部数据,生成字符(ASCII字符)频率表。然后构造Huffman树并生成与字符相对应的不等长编码。再将生成的Huffman编码转换为字符写入文件中。最后,将文件结尾倒数第五个字符标记为“H”,以标识压缩后的文件。解压缩时,将Huffman编码做逆变换后写入文件即可。

在数据通讯中,各码字的平均偏离方差直接影响到接收端的预留数据缓冲器的容量。当编码器经通信线路传送压缩数据流时,平均偏离方差很小的Huffman编码近似于恒定速度把每位编码送入缓冲器,增加了数据传输的准确度,同时也只需很小容量的缓冲器即可;平均偏离方差很大时,将使导入编码的输出码率不断变化,使每位编码进入缓冲器的速度不恒定,产生错误码的机率随之增大,同时也需要较大容量的缓冲器。

2 自适应Huffman编码

上述的Huffman编码是利用压缩对象出现频率的不等性进行编码的一种常用的无损数据压缩方法。不论从算法的复杂度还是在实现的难度以及对数据压缩的效果来看,Huffman编码都不失为一种较好的数据压缩算法。

Huffman编码假定压缩器事先知道字母表中所有符号出现的概率。而实用中,符号出现的频率绝少能预知。一个解决方法就是让压缩器读两次原始数据,第一次只是计算各符号的出现频率,第二次才压缩数据。在两次处理之间,压缩器构造Huffman树,这种方法称为半自适应的,但通常慢得无法实用,实用方法是自适应Huffman编码。

针对静态Huffman编码的上述缺点,提出了动态Huffman编码的算法。改进算法对数据进行编码的依据是动态变化的Huffman树,也就是说对第t+1个字符的编码是根据原数据中前t个字符得到的Huffman树来进行的。压缩和解压子程序具有相同的初始化树,每处理完一个字符,压缩和解压缩使用相同的算法修改Huffman树。动态Huffman编码算法克服了传统Huffman编码必须对文本进行两遍扫描的缺点,压缩效率大幅度提高。尤其对一些庞大的原文件而言,压缩和解压效率可以提高一倍至三倍。

2.1 首次出现字符的处理

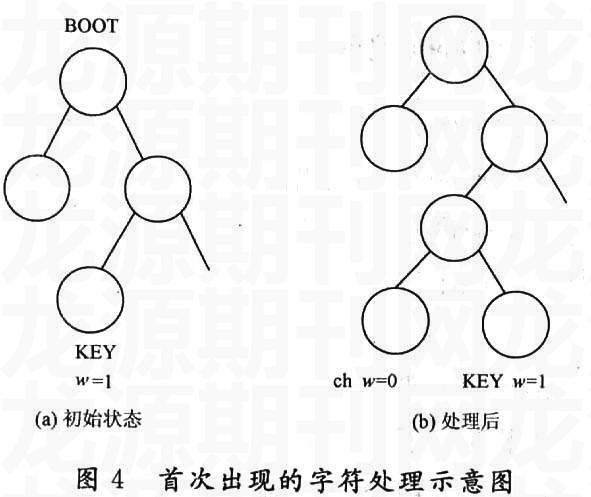
在动态Huffman编码中,第i个字符的编码是通过前i-1个字符所构成的Huffman树来求得的,哪些字符会出现事先无法知道,因此,当某个字符首次出现时,因它不在Huffman树中,无法对它进行编码,解决此问题的一个方法是,简单地将Huffman树初始化为权值为1的256个所有可能出现的码字符。这样,开始时每个字符的编码都是8位长,随着字符出现次数的增加,其编码位数将随之减少。但是,这在多数情况下会造成存储空间的浪费,降低数据压缩效果。为此,引入一个虚设的特殊字符‘KEY,用它来代替第一次出现的字符。当某个字符首次出现时,就用‘KEY所在的结点位置对它进行编码,并把编码写进目标文件。接着,把首次出现的字符的ASCII码值也写进目标文件。这样,就完成了首次出现字符的压缩处理。随后,要改变Huffman树的结构,让‘KEY代替下一个首次出现的字符。假定原先Huffman树的结构如图4(a)所示,当有一个字符首次出现时,就增加两个叶结点,它们分别作为‘KEY所在结点的左、右孩子。左孩子存放首次出现的字符,并令其权值为0,右孩子存放‘KEY,其权值仍为1,改变后的Huffman树如图4(b)所示。

图4 首次出现的字符处理示意图

同样地,在解压过程中,当还原出来的字符为‘KEY时,说明当时压缩的这个字符是首次出现的,接着往下连续读出8位(一个字符长),该字符就是所压的首次出现的字符。随后,使用与上述压缩过程中改变Huffman树结构的同样算法来改变Huffman树结构。

2.2 Huffman编码的更新

在动态Huffman编码中,第i+1个字符的压缩是由第i个字符压缩后所构成的Huffman树确定的。因此,每当压缩完一个字符,要随之更新Huffman树,它主要由权值的更改和调整两个步骤实现。

欲更改某个字符的权值,只要把该字符所对应的叶结点的权值增1,接着向上移至其父结点,把其权值也增1,同样的处理一直向上直至根结点。

Huffman树有一个重要的特性:树中任一个结点(根结点除外)的权值都小于或等于它上面任一结点的权值,并与它的兄弟相邻。当树中某个结点权值改变时,可能破坏这一特性。此时,就必须进行调整,使之仍为一棵真正的Huffman树。但是,权值改变未必破坏这一特性,因此这一步骤并不总是每次要执行。当某个结点的权值改变后,只要把当前结点的权值与它前一个结点的权值进行比较,若前者大于后者,则需要调整;否则不必调整。为了减少调整的工作量,向上查找,找到某权值小于当前结点的最远的一个结点,它就是所求的被交换结点,把当前结点与所求结点连同它们的左右子树(如果有的话)进行交换,就得到一棵正确有序的Huffman树。

2.3 两种编码方法的比较

下面对静态Huffman编码和动态Huffman编码方法稍作比较。静态Huffman编码的缺点在于需对原始数据进行两遍扫描第一遍扫描统计字符出现频率并建树,第二遍扫描根据所建Huffman树进行编码由此,在压缩时,将会降低压缩速度同时,为保存Huffman树以供解压时用,也将浪费一部分存储空间经验证明,由于静态建树,其压缩率也有所下降。

如前所述,动态Huffman编码对数据的压缩是依据动态变化的Huffman编码树,亦即对第i+1个字符的编码是由原始数据中前i个字符所建立的Huffman树确定的压缩和解压子程序具有相同的初始化树,每处理完一个字符,压缩和解压使用相同的算法更新Huffman树,不必为解压而保存Huffman树的有关信息,从而提高了数据压缩率。而且,由于只要一遍扫描就可完成压缩和解压处理,大大提高了压缩速度。但是,由于解压时采用与压缩时相同方法建树,增加了解压时间,从而降低了还原速度。而静态Huffman编码由于对Huffman树进行保存,还原时不必重新建树,节省了还原时间。应用所设计的压缩程序对多种类型的文件进行压缩并就压缩率加以比较,从而发现此压缩程序对文本文件的压缩率较高,对可执行文件等非文本文件的压缩率相对较低而且压缩率与文件长度有关,文件较长时其压缩率也随之下降,这正是动态Huffman编码数据压缩技术相对于其他压缩技术的一个缺点。

3 结 语

数据压缩是计算机科学中非常具有生命力的论题。一个好的数据压缩方法往往能够明显减少数据的存储空间,大大提高存储媒体的访问速度。

Huffman编码是数据压缩领域中最著名的编码方式之一。它通过对象频率出现的不等性,构造最优编码,达到减小文件大小的目的。目前广泛应用的许多其他高效的数据压缩算法(如算术编码,可预测编码等) 也是在Huffman编码的基础上发展起来的。所以,研究Huffman编码的思想,对于深入理解数据结构、程序设计等学科中的相关课题是十分有益的。特别是对动态Huffman编码算法的探索,尽可能使程序稳定、快速、高效地运行,充分体现了对软件时空需求进行优化与权衡的思想,这也是现代软件工程中十分重视的核心问题。

参考文献

[1]朱怀宏,吴楠,夏黎春.利用优化Huffman编码进行数据压缩的探索.微机发展,2004(6):1-6.

[2]Manoj Aggurwul,Ajui Nuruyun.Efficient Huffman Decoding.Applied Physics Letters,2000.

[3]张全伙,于洪斌,林榆.优化Huffman编码数据压缩技术及程序实现.华侨大学学报:自然科学版,1995(3):19-22.

[4]李伟生,李域,王涛.一种不用建造Huffman树的高效Huffman编码算法[J].中国图像图形学报,2005(3):18-21.

[5]刘金岭,刘国香.Huffman编码的优化.河北师范大学学报:自然科学版,2006,30(1):29-32.

[6]林建英,伍勇,李建华,等.一种易于硬件实现的快速自适应Huffman编码算法.大连理工大学学报,2008,48(3):436-440.

[7]包尔固德,李伟生.一种基于浓缩Huffman表的Huffman算法的研究与实现.微电子学与计算机,2007(11):31-33.