线性流形上矩阵方程(AX,XB)=(C,D)最小二乘自反解及其最佳逼近

张 敏，林卫国

(1.武汉军械士官学校 基础部，湖北 武汉 430075；2.武汉理工大学 机电工程学院，湖北 武汉 430070)

本文用Cm×n表示m×n复矩阵集，OCn×n为n阶酉矩阵集，0为零矩阵，AH与rank(A)分别表示复矩阵A的共轭转置与秩，‖·‖表示矩阵的Frobenius范数，A+表示矩阵的Moore-penrose广义逆，A*B表示A与B的Hadamard乘积，即当A=(aij),B=(bij)∈Cn×m时有A*B=(aijbij)∈Cn×m.

定义1[1]如果P∈Cn×n满足：(i)P=PH,(ii)P2=In，则称P为广义反射阵.

定义2[1]设P∈Cn×n为广义反射阵，称A∈Cn×n为关于P的自反阵(反自反阵)，若A=PAP(A=-PAP).

对于生产实践中的这样一类线性系统：AX=B,XD=E，其中A∈Cm×n,B∈Cm×p,D∈Cp×q,E∈Cn×q是给定的矩阵.1910年Cecioni[2]给出了该线性系统有公共解的充分必要条件，1984年Mitra[3]讨论了最小可能秩解，2006年盛兴平和陈果良[4]对此矩阵方程有公共解和无公共解时的情况做了详细的讨论.鉴于自反矩阵[5～7]具有很好的性质，且在工程和科学计算中有很广泛的应用，因此研究线性流形上该线性矩阵方程组的自反解对丰富矩阵理论、工程应用和科学计算都有重要意义.本文讨论如下两个问题：

(1)

问题1 求X∈S，使得‖AX-C‖2+‖XB-D‖2=min.

1 几个引理

引理1[1]设P∈Cn×n为广义反射阵，则存在U∈OCn×n，使得:

(2)

证明过程类似于文献[5]中定理1，显然S为线性流形.

2 主要结果

定理1 给定A,C∈Cm×n;B,D∈Cn×k,令:

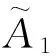
(3)

其中：

M1=(M11,M12)∈OCm×m,N1=(N11,N12)∈OCr×r,M2=(M21,M22)∈OCm×m,

N2=(N21,N22)∈OC(n-r)×(n-r),P1=(P11,P12)∈OC(r-t1)×(r-t1),R1=(R11,R12)∈OCk×k,

Γ1=diag(δ1,δ2,…,δr1),δi>0(i=1,2,…,r1),Γ2=diag(γ1,γ2,…,γr2),γi>0(i=1,2,…,r2),

∑1=diag(ξ1,ξ2,…,ξs1),ξi>0(i=1,2,…,s1),Σ2=diag(α1,α2,…,αs2),αi>0(i=1,2,…,s2),

M11∈Rm×r1,M21∈Rm×r2,N11∈Rr×r1,N21∈R(n-r)×r2,P11∈R(r-t1)×s1,P21∈R(n-r-t2)×s2,R11∈Rk×s1,R21∈Rk×s2,

则问题1的解的表达式为：

(4)

其中：

并且G1∈C(r-r1)×(r-t1-s1),G2∈C(n-r-r2)×(n-r-t2-s2)为任意矩阵.

证明由引理4以及U,Q1,Q2的酉不变性知:

‖AX-C‖2+‖XB-D‖2=

故‖AX-C‖2+‖XB-D‖2=min等价于:

(5)

(6)

(7)

由式(3)，(7)知:

故式(5)等价于:

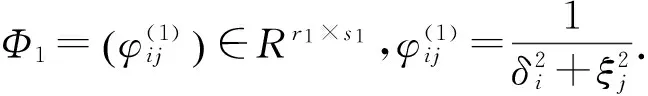
故问题1的解的表达式为(4)式.

(8)

其中:

证明由于:

故‖X-X*‖=min等价于:

(9)

(10)

由式(4)中Z1表达式知:

[1]陈景良,陈向晖.特殊矩阵[M].北京：清华大学出版社，2001.

[2]Cecioni F.Sopra operazioni algebriche[J].Ann Scuola Norm Sup Piss Sci Fis MAT,1910,11:17-20.

[3]Mitra S K.The matrix equationsAX=B,XD=E[J].Linear Algebra and Its Applications,1984,59:171-181.

[4]盛兴平,陈果良.矩阵方程AX=B,XD=E解的研究[J].兰州大学学报,2006，42(3):101-104.

[5]Peng Z Y,Hu X Y.The reflexive and anti-reflexive solutions of the matrix equation AX=B [J].Linear Algebra and its Applications,2003,375:148-155.

[6]张磊，谢冬秀.一类逆特征值问题[J].数学物理学报，1993，13(1):94-99.

[7]Chen H C.Generalized reflexive matrices special prosperities and applications [J].SIAM J Matrix Anal Appl,1998,19:140-153.