两个三角函数积的和的封闭形和式

及万会,李忠宁

(银川大学数学教研室,银川永宁750105)

文献 [1]讨论了,正,余弦函数奇偶次方的积和式.文献 [2,3]给出一些特殊角三角函数数方幂和.文献 [4,5]研究由Lucas序列构造组合恒等式,以及最大公约数和最小公倍数的和问题.本文利用发生函数方法得到首先得到一类三角函数序列封闭形和式计算公式和正负相间封闭形计算公式.其次利用复数隶莫弗乘法公式得到两个三角函数序列的乘积封闭形和式表达式.若无特别说明,文中字母表示正整数.

熟知有理分式化成部分分式有下列结论.

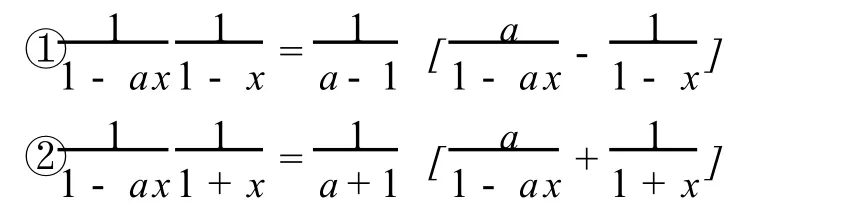
定理1 sin(kα+φ),cos(kα+φ)为三角函数,复数 d≠0,d≠a-1,b-1则含有等比数列的三角函数封闭形和式为:

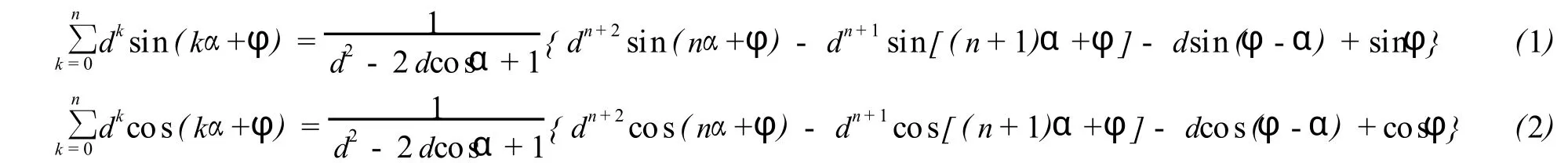
若d≠-a-1,-b-1.则含有等比数列的三角函数封闭形和式为:

注意到,若 d≠-a-1,-b-1,则 (ad-1)(bd-1) ≠0

比较D(x)两端xn系数,得到式 (3).类似式 (3)式方法得 (4)式.定理1证毕.

定理2 两个三角函数积的封闭形和式

两个复数相乘: (1)实部与实部相乘+虚部与虚部相乘,利用三角函数公式cos(α-β)=cosαcosβ+sinαsinβ,整理化简与 (1)式左端实部相等得 (5)式 (2)前一复数实部乘以后一复数虚部+前一复数虚部乘以后一复数实部利用三角函数公式sin(α-β)=sincosβ-cosαsinβ整理化简与 (1)式左端虚部相等得式 (6).同法利用式 (2)得式 (7)、(8).利用式 (3)、(4)分别得式 (9)、(10)与 (11)、(12).

[1] 杨存典,刘端森.正,余弦函数奇偶次方的积和 [J].商洛学院学报,2007,(02)：8-10

[4] 及万会,黑宝骊.由Lucas序列推导组合恒等式 [J].河北北方学院学报：自然科学版,2008,(04)：3-5

[5] 及万会,张来萍,黑宝骊.最大公约数和最小公倍数的和 [J].河北北方学院学报：自然科学版,2007,(03)：4-6