模糊图像的最大熵恢复

陈春涛，黄步根

（江苏警官学院 公安科技系，江苏 南京210012）

引言

在刑事技术领域，各种图像信息（其内容包括指纹，足迹，各种工具痕迹，枪弹痕迹以及现场照片，监视录像等）具有很重要的证据作用，有时甚至是侦查破案的关键。但是，这类图像信息经常会受图像获取过程中的一些因素的影响而产生“降质”，即变得模糊甚至难以辨读。因此，在司法鉴定中，运用图像恢复技术对模糊图像进行恢复处理，提高其证据价值，具有重大的现实意义。

导致图像模糊的因素一般包括对焦不准，相机在曝光时与被摄物体的相对运动，光学系统本身的缺陷，以及感光介质（胶片或光电器件）的噪声等。离散形式的图像降质过程通常可用如下的模型描述：

这里，矩阵Y，X和N分别表示含噪声的模糊观测图像，原始清晰图像和加性噪声。矩阵H代表成像系统的点扩展函数（Point Spread Function，PSF）。符号“*”表示二维卷积运算。图像恢复的任务就在于根据已经得到的受噪声N和其他降质因素影响的观测图像Y，来求得对于原始清晰图像X的最佳估计。

在众多的图像恢复方法中，最大熵方法因其优于一般线性恢复方法（如维纳滤波法等）的恢复质量而占据着重要的地位。最大熵方法的一般数学模型如下：

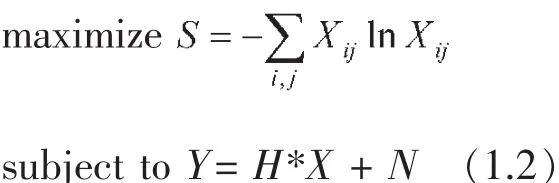
其中，Xij表示X的元素，S表示图像X的熵，这一图像熵的表达式最早由Frieden[1]提出，与Shannon在信息论中提出的信息熵具有相同的形式。当然，还有一些学者提出了其他形式的一些图像熵表达式[2]。

这一最大熵问题可以通过许多不同的方法求解，从而形成一系列的最大熵算法[3，4，5]。我们在经过比较研究后选择了由Hollis等提出的算法，因为该算法具有处理效果良好，简明且稳定收敛的特点。

1 Hollis等的最大熵算法

此算法仅考虑无噪声的情况（或者说将噪声与信号同样看待）。运用拉格朗日乘数法解式（1.2）可以推出：

其中矩阵λ由拉格朗日乘子构成。从一个初始的λ0=0（对应于一个“平坦”的，即具有最大熵的初始图像）开始，可以构造出如下的迭代算法：

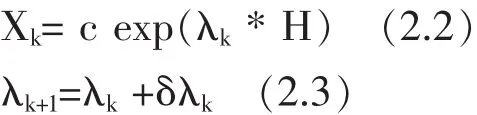
其中，c是比例常数，δλk为λk的改变量。一开始，Hollis等定义δλk为：

但是那样收敛很慢。后来发现用下式可以加速收敛：

本文在研究中采用了由David S.C.Biggs等提出的对于图像迭代恢复算法的加速方法[7]，实践表明其加速效率和恢复效果优于（2.5）式。

2 图像恢复实例

本文用MATLAB与VC混合编程实现了上述算法，并针对大量的模糊图像（包括人工模拟的和实际拍摄的模糊图像）进行了恢复处理，取得了良好的效果。

2.1 运动模糊车牌图像的恢复

图1是一张快速行驶中的卡车照片，车牌号码严重模糊，无法辨认。剪取车牌部分（如图2（a）所示）进行恢复，其中运动方向和长度可以通过画面上运动客体的边缘部分的影像估计出来，并由此根据二维直线运动模糊的PSF的数学模型得到相应的点扩展函数。恢复结果（如图2（b）所示），可以看出，车牌号码已经变得很清楚。

图1 原始运动模糊图像

图2 运动模糊车牌的恢复

2.2 运动模糊人脸图像的恢复

图4（a）是一张骑车男子的照片。由于拍摄时快门速度较慢，导致其面部影像严重模糊，无法辨认。根据衣领的运动轨迹估计出影像在曝光过程中的运动方向和长度。由此确定出点扩展函数。用加速的最大熵方法迭代15次恢复的结果（如图4（b）所示）。可以看出，尽管存在一些因边界效应引起的震荡，该男子的五官已可以辨认。

图4 运动模糊人像的恢复

2.3 离焦模糊照片的恢复

图5是一个表现弹壳底部痕迹的照片，这类照片在公安工作的实践中经常会遇到。由于在拍摄时没有仔细地对焦，因而画面有点模糊，弹底的细节不是很清晰。图6是运用本文的最大熵方法进行恢复的结果。可以看出，画面模糊的程度显著减轻，照片表现出了更多的弹壳的细节。处理前，通过对图像频谱的过零点的考察确定出离焦半径，进而得到PSF的估计。

图5 原始模糊图像

图6 最大熵恢复结果

2.4 离焦模糊人脸图像的恢复

图7（a）是一个用CANON G5数码相机拍摄的人脸照片（手动对焦）。图7（b）是其恢复结果。处理前，通过对图像功率谱的过零点的考察确定出离焦半径，进而得到PSF的估计。经过18次迭代，图像表现出更多的细节特征。

图7 离焦模糊人像的恢复

3 结论

实践表明，本文的最大熵算法是有效的、稳定的，完全可以应用于司法领域的图像处理。需要指出的是，运用这一算法恢复含噪声的图像时，随着迭代次数的增加，噪声放大的情况也变得严重。这可能是由于算法没有对噪声单独考虑，而是把它与信号同样看待的原因。因此，实际处理时需要在适当的时候停止迭代以取得最佳恢复效果。在软件设计时，我们通过在每次迭代结束时实时显示图像并进行交互控制的的方法（即对恢复结果进行连贯显示）解决了这一问题。

[1]B.R.Frieden.Restoring with maximum likelihood and maximum entropy[J].Opt.Soc.Am，1972，62:511-518.

[2]E.Pantin，J.L.Starck.Deconvolution of astronomical images using the multiscale maximum entropy method[J].Astron.Astrophys.Suppl.Ser.1996，（9）:515-585.

[3]J.M.Hollis，J.E.Dorband and F.Yusef-Zadeh.Compare restored HST and VLA imagery of R ARUARⅡ[J].The Astrophysical Journal，1992，386:293-298.

[4]S.F.Gull and J.Skilling.MEMSYS5 User's Manual[M].Version 1.2.Suffolk，U.K，1999.

[5]X.Zhuang，E.Ostevold，and R.M.Haralick.A differential equations approach to maximum entropy image reconstruction [J].IEEE Trans.1987，35:208-218.

[6]陈春涛，黄步根，陶纯堪，等.最大熵图像复原及其新进展[J].光学技术，2004，（1）:12.

[7]David S.C.Biggs and Mark Andrews:Acceleration of iterative image restoration algorithms[J].Applied Optics.1997，36，（8）：1766-1775.