一个以自更新为主的林龄发展系统

徐龙封，李 俊

（安徽工业大学 数理学院，安徽 马鞍山 243002）

一个以自更新为主的林龄发展系统

徐龙封，李 俊

（安徽工业大学 数理学院，安徽 马鞍山 243002）

讨论了一个以自更新为主的林龄发展系统，并利用特征线法和积分方程理论，证明了这个系统初边值问题古典解的存在唯一性。

自更新；林龄系统；发笋率；积分方程

森林具有十分重要的经济、防护、生态和社会效益，与人类的生存、繁衍、发展关系及其密切。近几年来，对森林发展系统的研究，吸引了很多科技工作者的兴趣。人们提出了很多森林发展系统模型[1-13]。一般森林系统的基本特点是通过造林更新来维持其发展，但对例如竹林这样以自更新为主的林龄发展系统目前还未见到有人研究。下列模型：

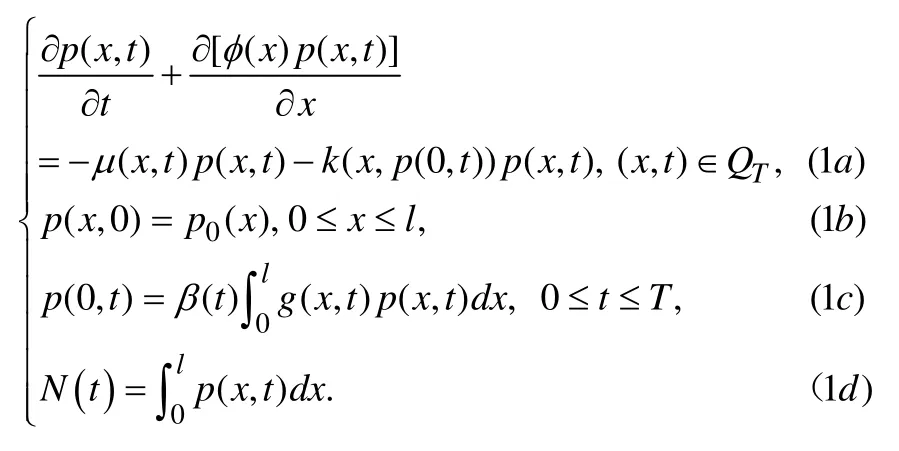
表示在时刻t林龄为x的竹子在单位时间内平均采消面积与剩余的面积之比。显然在任何时刻 t，只有林龄达到l的竹子才全部采伐，而保持竹林中具有林龄在0到l之间的各种竹子。即对任意

1 定理1的存在性证明

2 定理1的唯一性证明

[1] 陆征一，周义仓. 数学生物学进展[M]. 北京：科学出版社， 2006，4: 251-264.

[2] 于景元, 等，林龄面积转移方程解的性质[J]. 应用数学学报，1994，17(4)：606-612.

[3] 王定江.非线性种群发展方程解的性质[J].高校应用数学学报，1998,13(1)：23-30.

[4] 高德智，许香敏. 森林发展系统中的更新成林率的辨识问题[J]. 系统工程理论与实践，1999,19: 90-93.

[5] 李留瑜, 等. 论森林的数量结构[J].系统工程理论与实践，1996,16：82-89.

[6] 徐龙封. 一类线性纯林发展系统对总量控制的问题[J].巢湖学院学报，2008, 10(6): 1-5.

[7] 张启敏，聂赞坎. 森林发展系统强解的存在唯一性及稳定性分析[J].生物数学学报，2004,19(4)：51-56.

[8] 郑治刚，同龄纯林的林龄分布结构变化方程[J]. 系统工程理论与实践，1996, (16)4：90-98.

[9] XU Long-feng, WU Han-bing. A free-boundary problem to dynamic system for pure forest[J]. Ann. Of Diff. Eqs. 2010,20(2): 227-233.

[10] Allen L J S. Discrete and continuous models of populations and epidemics[J]. J.Math. Sys. Estim. Control,1991,1:335-369.

[11] Angel C, Joan S. Global dynamics and optimal life history of a structured population model[J]. SIAM J. Appl. Math., 1999, 59(5):1667-1685.

[12] Ballinger G & Liu X, Permanence of population growth models with impulsive effects[J],Math. Comp. Modeling,1997, 26:59-72.

[13] Wang D J. & Zhang Y F. T he property of solution of a nonstationary forest evolution system[J],Systems Science and Systems Engineeing,1993,2: 281-288.

[14] O. A. Ladyzenskaya,Linear and quasilinear equations of parabolic type[M].Translations of Mathematical Monographs, A. M. S. Providence, Provience.Rhode Island Translated from the Russian by S. Smith, 1968 (23): 3-9.

[15] 沈以淡. 积分方程[M].北京: 北京理工大学出版, 2002, 6(2):18-22.

[16] 王元明，徐君祥. 索伯列夫空间[M]. 南京：东南大学出版社，2003,8.

A Stand Age Dynamics System Chiefly Relying on Self-renewal

XU Long-feng，LI Jun
(School of Math.& Phys., Anhui University of Technology, Ma’anshan Anhun 243002, China)

A stand age dynamics system chiefly relying on self-renewal is discussed in this paper. The existence and uniqueness of the classical solution to boundary value problem of this system are demonstrated by applying method of characteristic curves and theory of integral equation.

self-renewal；stand age system；natality rate of bamboo shoot；integral equation

O175.12；O175.1

A

1009－5160(2010)03－0029－04

徐龙封（1952-），男，教授，研究方向：偏微分方程.

国家自然科学基金（90410011）；安徽省教育厅重点自然科学基金（KJ2010A043）；安徽工业大学研究生创新研究基金项目.