利用岩屑测量泥页岩物理化学参数

王京印 苏新亮 方国印 张晓春 李 蕾

(1.中国石油大学(华东)石油工程学院,山东东营 257061;2.中国石油天然气股份有限公司,北京 100007;3.中海油田服务股份有限公司,天津 300452)

泥页岩渗透率和膜效率是泥页岩井壁稳定力学化学耦合分析中极其重要的参数[1-3]。泥页岩的渗透率和膜效率是通过力学化学耦合作用下的压力传递试验获得的。这种耦合过程的压力传递试验研究从20世纪90年代起直到2005年这段时间内一直没有间断[3-6],但是,多数研究都是在努力改进、提高仪器的精度,而对泥页岩膜效率的测量方法一直没有深入研究。

笔者对利用岩屑测量泥页岩渗透率和膜效率的方法进行了试验研究,研制了岩屑测量泥页岩渗透率和膜效率的仪器,给出了计算泥页岩渗透率和膜效率的新方法,利用研制的仪器和给出的计算方法进行了岩屑渗透率和膜效率的测量,并与岩心测量结果进行了对比。

1 试验仪器及测量方法

1.1 试验仪器及工作原理

通常情况下,现场可以得到厚度约1 mm的岩屑。为能够在钻井施工现场快速方便地测量渗透率和膜效率,笔者研制了便携式钻屑物理化学参数测试系统,如图1所示。该系统主要由压力容器、轴向加压系统、液体循环系统、数据采集系统等部分组成。测量时,将岩屑置于压力容器内,上下两端施加轴向压力固定,同时利用液体循环系统施加孔隙压力。试验分为水力压力传递和耦合作用压力传递两个阶段。利用水力压力传递阶段的试验数据可以计算出岩屑的渗透率,利用耦合作用下的压力传递阶段的试验数据可以计算出岩屑的膜效率。

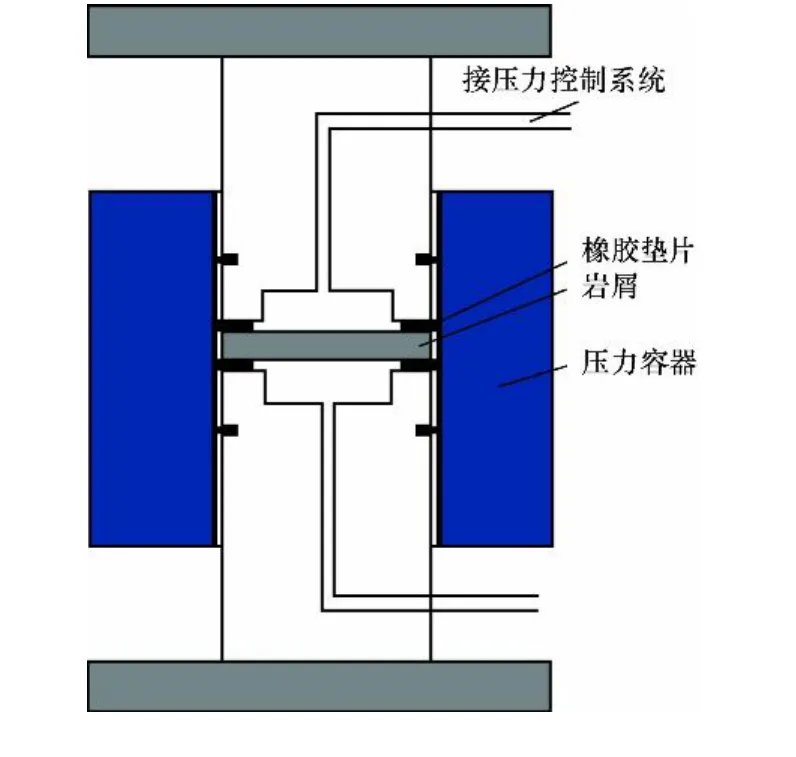
图1 便携式钻屑物理化学参数测试系统基本结构

1.2 测试方法和步骤

1)岩屑的安装与固定。选取厚度为1～2 mm、直径5～10 mm的岩屑(这样的岩屑在现场是极易获取的),然后安装和固定在测试仪器中。

2)逐级交替施加轴向压力和液体循环压力,以免岩屑应力过分集中而破碎。

4)水力压差作用下的压力传递。增加上端压力到钻井液液柱压力,并维持压力值恒定;下端压力保持为地层孔隙压力 pp,这一阶段连续进行直至下端压力接近上端压力,并记录下端的压力变化情况,用于计算岩样的渗透率。

5)耦合作用下的压力传递。水力压差作用下压力传递试验结束后,更换顶端溶液,换溶液过程中应使岩样两端压力相等。记录在耦合作用下,下端压力的变化情况,进一步研究水在耦合作用下的运移规律,并用其计算岩屑的膜效率。

2 渗透率及膜效率的计算方法

2.1 渗透率的计算方法

由于泥页岩的渗透率非常低,因此不能用常规的渗透率测量仪器分析。通常文献介绍的利用岩心测量泥页岩渗透率的原理为:将水在泥页岩中的渗透过程比拟为压力扩散过程,根据达西定律和压力扩散方程对泥页岩渗透率进行推导[2,7],推导出的公式为:

式中,K为泥页岩渗透率,μm2;β为流体静态压缩率;μ为流体黏度,mPa·s;V为测试仪器岩样下游容器体积,cm3;l为岩样长度,cm;A为岩样横截面积cm2;pm为岩样上端压力,MPa;po为岩样孔隙压力,MPa;p(l,t)为下端 t时刻的压力,MPa;Δt为时间差,μs。

利用瞬态压力传递技术,对泥页岩渗透率进行了测定。在求取泥页岩渗透率参数时,首先需要获得测试仪器岩样下游容器体积V的具体数值。通常这个测量值容易产生误差,导致渗透率计算结果不准。而岩屑测量装置更无法测量下游容器体积,因此必须建立新的渗透率计算方法。

笔者采用渗流方程参数反演方法求取泥页岩的渗透率。水力作用下孔隙流体的流动方程为:

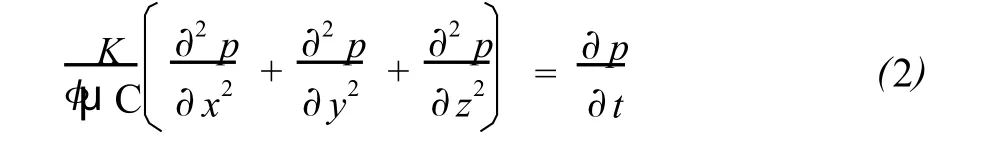
一维情况下方程为:

式中,Φ为孔隙度,%;C为流体压缩系数,MPa-1。

式(2)为水力作用下的压力传递方程,利用试验得到的指定位置的压力变化曲线,可以采用反演法求出渗透率。图2为典型的水力作用下岩样下端的压力变化曲线。

图2 水力作用下压力变化曲线

2.2 膜效率的计算方法

近几年,国内外出现了一些关于膜效率测量方法的文献[5,8],但常规的膜效率计算方法存在一定缺陷。原因在于:试验证明,用以测量膜效率的试验过程本身就是一个力学-化学的耦合流动过程,而文献中均认为是单纯化学作用的压力传递过程。要想正确计算膜效率,必须在耦合流动方程的基础上,采用反演法求出膜效率。为此,笔者进行了建立膜效率计算新方法的研究。

力学化学耦合作用下孔隙流体的流动方程为[8]:

化学势分布方程为:

式中,D为化学势扩散系数,s-1;θ为化学势。

在实验室测定中,可以作为一维处理,因此流动方程和化学势分布方程可写为:

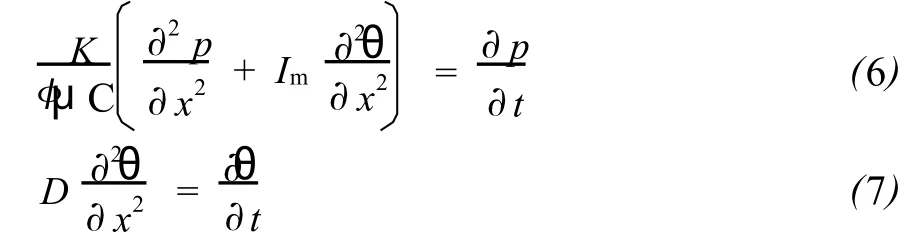
初始条件:

边界条件:

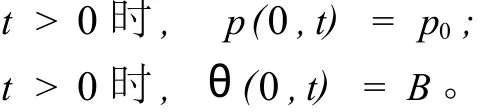
式(6)为流-化耦合作用下的压力传递方程。在除膜效率外其他参数已知的情况下,利用试验得到的指定位置的压力变化曲线(图3为典型的耦合作用下岩样下端压力变化曲线),利用式(6)反演求膜效率是一个典型的微分方程反问题,求解方法在很多微分方程专著上都有介绍。若岩石非均质,系数Im为变量,即 Im是 x或者t的函数,则该类问题可用PST脉冲谱法求解。若系数 Im为定值,求解方法相对简单得多。在笔者所研究的问题中系数 Im为一定值。求解方法类似PST脉冲谱法,具体步骤如下:

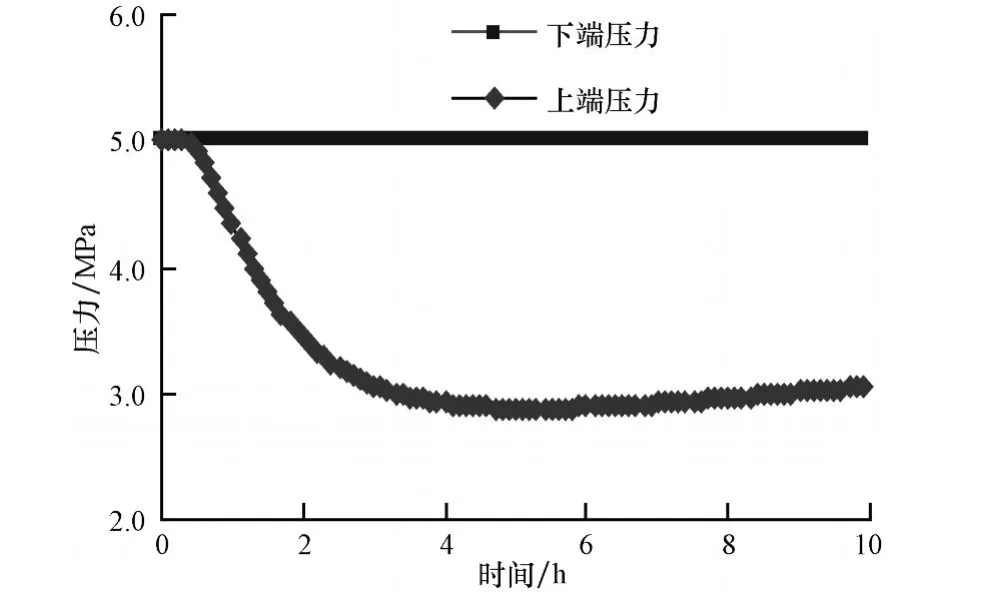
图3 耦合作用下的压力变化曲线

1)首先给定待定系数的初始猜测值 Im0,并令n=0;

2)采用有限差分法或者有限元法求解微分方程式(6);

3)求解 x=L,即试验岩石下端处压力 p随时间的分布;

4)将计算得到的 p值与测量得到的 p值进行比较;

5)如果比较结果不满足精度要求,则令 Im1= Im0+nΔIm(n=n+1),返回2)重新计算;否则迭代停止。

3 测量结果及验证

为验证岩屑测量结果的可靠性,笔者分别利用不同钻井液对6块岩屑以及对应的岩心进行了相关试验,结果见图4、图5。从图4、图5可以看出,利用岩屑测量的渗透率和膜效率与利用岩心测量的渗透率和膜效率具有良好的一致性,数据在直线y=x附近波动,相关系数R接近1,最大相对误差不超过10%。这说明利用岩屑测量的渗透率和膜效率是可靠的,能够代表所研究岩石的渗透率和膜效率。

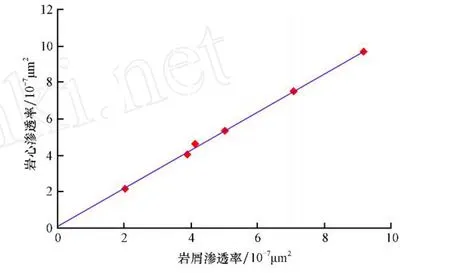
图4 岩屑、岩心渗透率对比

4 结 论

1)利用岩屑测量泥页岩的渗透率和膜效率是可行的。

2)利用岩屑测量得到的泥页岩的渗透率和膜效率是可靠的。

3)利用岩屑测量泥页岩渗透率和膜效率方便、快捷、准确,更适合于现场应用。

[1] 邓虎,孟英峰.泥页岩稳定性的化学与力学耦合研究[J].石油钻探技术,2003,31(1):33-35

[2] 徐加放,邱正松,王瑞和,等.泥页岩水化应力经验公式的推导与计算[J].石油钻探技术,2003,31(2):33-35

[3] 徐加放,邱正松,秦涛,等.泥页岩压力传递性的实验研究[J].石油钻探技术,2004,32(1):23-25

[4] 屈沅治,孙金声,苏义脑.新型纳米复合材料的膜效率研究[J].石油钻控技术,2008,36(2):32-35.

[5] Tan C P,Rahman S S,Richards B G,et al.Integrated rock mechanics and drilling fluid design approach to manage shale instability[R].SPE 47259,1998.

[6] Muniz E S,da Fontoura S A B,Lomba R F T.Rock-drilling fluid interaction studies on the diffusion cell[R].SPE 94768,2005.

[7] Tan C P,Waverley G V,Rahman S S.The mechanism of mud support reduction due to mud pressure penetration[R].SPE 28063,1994.

[8] Tan C P,Richards B G,Rahman S S.Managing physico-chemical wellbore instability in shales with the chemical potential mechanism[R].SPE 36971,1996.