月球车全局路径规划中的A*算法改进

彭 松 贾 阳

(北京空间飞行器总体设计部,北京 100094)

1 引言

月球车是进行月表探测的一种有效工具,在其巡视探测期间,一个重要的工作就是进行路径规划[1]。路径规划分为基于地图的全局路径规划和基于传感器的局部路径规划。所谓全局路径规划,是在环境完全已知的情况下,依据某个或几个优化准则(如路径最短、时间最少等)来寻找全局最优路径。全局路径规划的算法有很多,如遗传算法、蚁群算法、神经网络算法、波形算法、A*算法等。A*算法是一种状态空间启发式算法,由于其搜索效率相对较高且容易实现, 在智能车辆上得到广泛的应用[2-5]。美国火星探测漫游车(M ER)采用的Field D*算法就是一种动态的A*算法,它利用了A*算法的高效性,又采用动态搜索来解决环境信息不完整的问题[6]。但是A*算法只是一种“较优”的算法,即它一般只能找到较优路径,而非最优路径[7],特别是在存在凹形障碍的情况下,它的搜索路径更为曲折。

本文是在环境信息完全已知的情况下对月球车进行全局路径规划,针对传统A*算法搜索速度慢和返回路径不够优化的不足,先对算法流程进行改进,提高其搜索效率,优化其返回路径,解决凹形障碍中规划失败的问题,然后使用二次搜索策略对存在凹形障碍情况下的规划路径进行优化,达到输出最短路径的目的。

2 A*算法改进

2.1 A*算法思想和算法流程

A*算法是在广度优先搜索的基础上引入了一个估价函数,每次都利用这个估价函数对所有可展点进行评价, 从而找出最优的可展点,再从该点进行搜索直至找到目标点[8]。估价函数表达式为:

f(n)=g(n)+h(n), 要求启发函数h(n)≤h*(n)

f(n)——从起点经过节点n 到达目标点的全程路径代价预测值;

g(n)——从起点到达节点n 的路径代价实际值;

h(n)——从节点n到达目标点的路径代价估计值;

h*(n)——从节点n 到达目标点的路径代价实际值。

f 值最小的可展点视为最优。

传统的A*算法流程[9]如下:

步骤1:初始化, 生成一个OPEN 列表、一个C LOSED 列表。

步骤2:把起点加入OPEN 列表。

步骤3:如果OPEN 列表为空,则失败退出,否则进行步骤4。

步骤4:遍历OPEN 列表,查找f 值最小的点,将其移入CLOSED 列表,并把它作为当前点。

步骤5:判断当前点是否为目标点,若是,则规划结束,输出路径;否则将当前点的相邻点投入OPEN 列表,进行步骤3。

步骤6:保存并输出C LOSED 列表中的路径节点。

2.2 改进的A*算法

改进后的A*的算法流程如下:

步骤1:初始化, 生成一个OPEN 列表、一个C LOSED 列表和一个FA THER 列表,初始值都为空;标记所有点的open 值为0。

步骤2:把起始点加入OPEN 列表,标记该点的open 值为1(表示该点进入过OPEN 列表)。

步骤3:如果OPEN 列表为空,记下当前点为坏点,若坏点为起始点,则失败退出,否则将坏点的父节点(若B 点最初由A 点展开一次得到,则称A 是B 的父节点)置为当前点,跳过步骤4 直接执行步骤5。

步骤4:遍历OPEN 列表,查找f 值最小的节点,将其移入C LOSED 列表,并把它作为当前点;同时清空OPEN 列表。

步骤5:判断当前点是否为目标点,若是,则规划结束,输出路径;否则对于当前点展开的每一个相邻点进行如下操作:

情况1:它是障碍点或者在CLOSED 列表中,剔除它,查找下一相邻点;

情况2:它的open 值为1(说明它加入过OPEN列表,其父节点已经设置),计算该节点的f ,g 和h值;

情况3:它的open 值为0,把它加入OPEN 列表,同时将其open 值记为1,并且把当前点设置为它的父节点,计算该节点的f ,g 和h 值。

然后进行步骤3。

步骤6:保存并输出路径,从目标点开始,每个节点沿着父节点移动直至起点,即FA THER 列表中的路径节点。

2.3 改进说明

比较改进前和改进后的算法流程,这里主要做了5 点改进:

1)为了减少排序节点的个数,提高算法的执行效率,在对所选节点的相邻点进行展开时,可首先排除已经在CLOSED 列表中出现的节点[10]。这在路径规划上的结果就是不允许返回走过的路径,有效地避免了迂回。有一点值得指出的是,在没有排除可展节点中已经在C LOSED 列表中出现的节点时,经常会出现在某两个节点之间来回振荡的情况,从而使程序陷入死循环,改进后则从根本上避免了该种情况。

2)对所选节点的相邻点进行展开后, 先将OPEN 列表中元素清空, 再把这些展开点投入OPEN 列表。这样做有两个好处:

一是OPEN 列表中的元素不会因为累加而越来越多,而是有一个上限,这个上限为节点的所有相邻节点数。这样在挑选OPEN 表中f(n)最小的节点时,会显著减少循环次数,提高执行速度。

二是从OPEN 表中投入CLOSED 表的相邻节点必是物理上的相邻,不会出现跳跃,从而保证规划路径的连续性。

3)关于改进后流程中的步骤5 中情况2 情况,文献[10]指出:若展开点进入过OPEN 表,检查这条路径(即经由当前点到达该展开点)是否更好,用g 值作参考,更小的g 值表示这是更好的路径。如果g 值更小,把当前点设置为它的父节点,并重新计算它的g 和f 值;否则g 和f 保持不变。但是实际上不会出现g 值更小的情况,因为后搜索到节点的g 值总是大于先搜索到节点的g 值,所以g 和f 值总是保持原来的较小值。由此在选择OPEN表中最小f 值的节点时,总是倾向于选择先搜索到的离起始点近的节点,造成CLOSED 表中返回的搜索路径向起始点迂回

本文采用的方法是无论展开点是否进入过OPEN 列表,都重新计算g 值和f 值,然后选择f值最小的节点。在路径规划上的体现是,每走一步都是最优的,并且此步最优是建立在上步最优的基础上,通过步步最优来返回CLOSED 列表。

4)返回路径时,不是将CLOSED 表中的元素逐一列出,而是从目标点开始逐个返回父节点投入FA THER 列表,直至到达起始点,这样可显著减少返回节点, 缩短了路径。在编程时, 可以对每个OPEN 表中的节点建立指针指向它的父节点,最后通过指针找到它的父节点。

5)对于步骤3 的改进,主要是针对地图中存在凹形障碍的情况。当地图中存在凹形障碍时,搜索路径往往会掉入凹形陷阱,由于程序中规定后续搜索节点不能是先前进入CLOSED 列表中的点,有时造成搜索路径卡死在陷阱中,导致规划失败。在这一特殊情况下,采取的策略是路径从卡住的坏点后退一步到达其父节点,尝试其他的可展节点,如果失败再后退一步接着尝试,直至到达目标点。

2.4 仿真算例

2.4.1 路径规划模型的建立

仿真是在假设环境信息完全已知的情况下做的。仿真输入是一个二维栅格地图,用栅格的中心点代表整个栅格,称为节点[11]。每个节点有两个状态:可通行点和障碍点。如图1 所示,“点”表示可通行点,上三角形表示障碍点(下同)。每个节点可以向四周八个方向的相邻节点移动。需要指出的是,从点5 到点7 的连线与障碍点4 所代表的栅格相切,这里认为是可通过的。实际应用中,把真实障碍外扩一定距离,变为扩展障碍,以保证点5、7 连线的可通过性。

图1 地图中的栅格和节点Fig.1 Grids and nodes in map

评价函数的选择:

f(n)=g(n)+h(n),其中

这里取α=1.4,β=1.0,因为相邻点的对角线方向距离和水平垂直方向的距离比值是2;

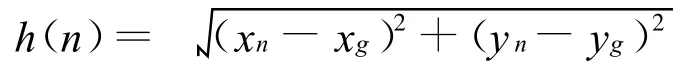
这里取的是当前节点(xn,yn)和目标点(xg,yg)的直线距离。

2.4.2 针对改进的仿真结果

对于改进1)和2),它减少了每次参加排序的节点数,使得运算加快,显然提高了搜索效率。

对于改进3)和4),图2 给出了不失一般性的例子,从图2(a)和图2 (b)可以看出,文献[10]方法返回的路径向起始点迂回,本文方法表现较好;从图2(b)和图2(c)可以看出, FA THER 列表返回的路径要优于CLOSED 列表的返回路径。

对于改进(5),不失一般性,图3 给出了一个存在凹形障碍的仿真实例。如图3 (a)中的A 点所示,由于程序规定后续扩展节点不能是先前进入CLOSED 列表中的点,即不能返回B 点,而与A 点相邻的其他点又都是障碍点,从而造成路径卡在A点,无法继续扩展,导致规划失败。在这一特殊情况下,采取的策略是从卡住的坏点后退一步到达其父节点,尝试其他的可展节点,如果失败,再后退一步接着尝试,直至跳出凹形障碍。如图3(b)所示,路径从A 点后退到其父节点B,B 点依然没有可扩展点,仍是坏点;路径再退一步到达B 点的父节点C,C 点有两个可展节点D 和E;下一步选择D 点,从而跳出了凹洞,继续搜索趋向目标点。

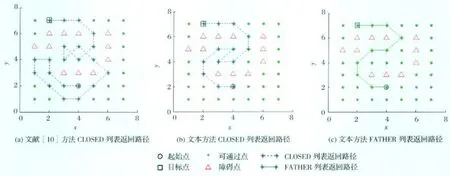
图2 仿真算例比较Fig.2 Com parison of simulation results

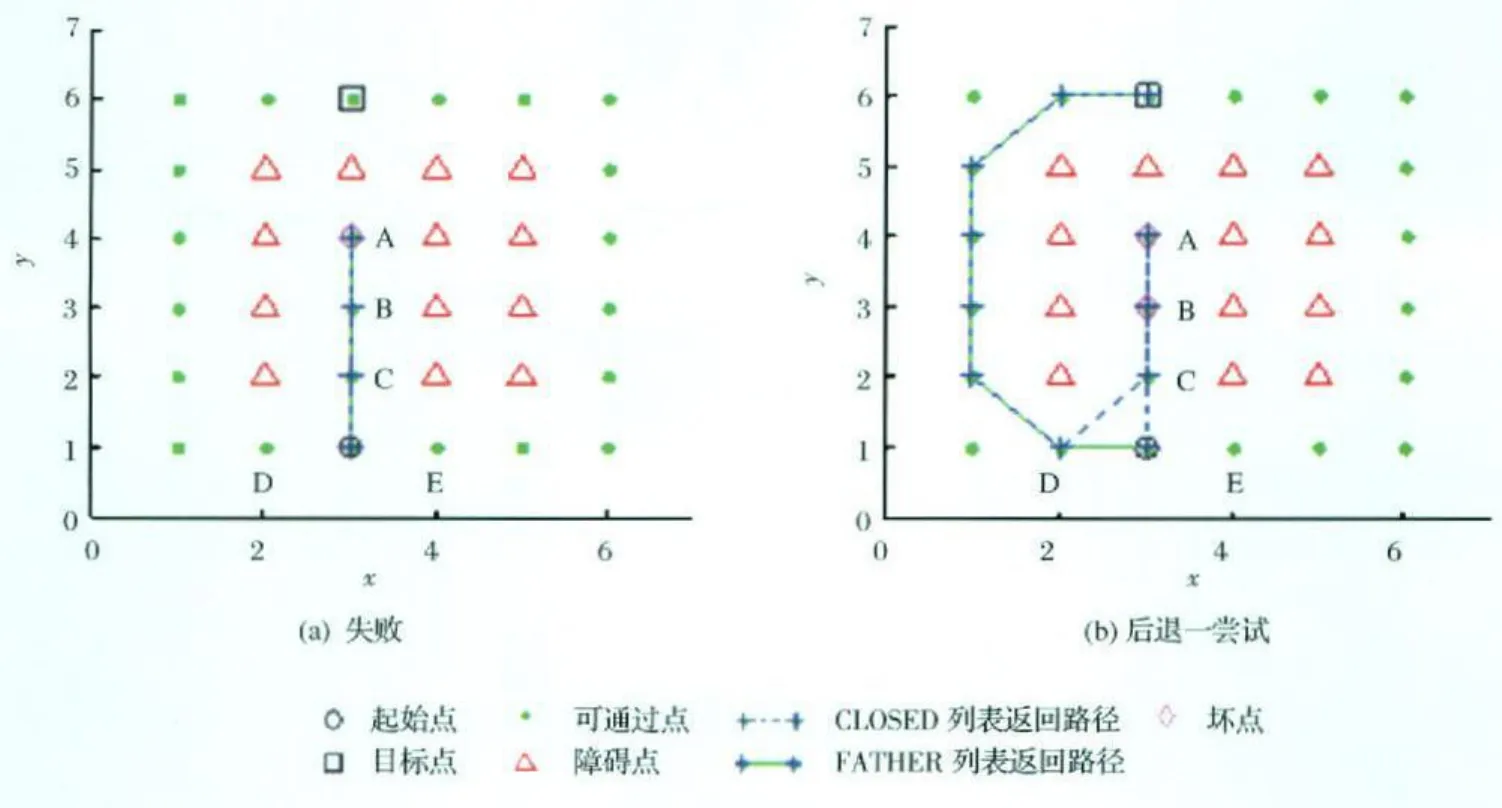
图3 存在凹形障碍物的路径规划Fig.3 Path planning with concavity obstacles

3 双向二次搜索策略

对于只存在凸形障碍的地图,改进的A*算法能快速地得到一条最优路径,但是对于存在凹形障碍的地图,返回的路径不够优化。

不失一般性,图4 给出了一个含有凹形障碍的地图。如图4(a)所示,CLOSED 列表返回的路径首先到达凹洞最底部,发现前方无法通过后,扩展点只能向两侧或后方延伸。由于启发信息h(n)是当前点和目标点的直线距离,CLOSED 列表中的扩展节点连线近似为:以目标点为圆心一层一层地向外画圆弧直至走出凹形障碍,然后趋向目标点。这种沿圆弧层层外扩的结果使得CLOSED 列表遍历凹形障碍的内部节点。

FATHE R 列表返回的路径比C LOSED 列表的路径有很大改观,近似为沿直线进入凹洞底部然后又沿直线跳出,但是依然没有避免陷入凹洞,路径不够优化。

采用二次搜索策略优化路径。在第一次搜索的基础上,将首次搜索CLOSED 列表中返回的节点看作可通过点,地图中的其他点都视为障碍点,重新构建地图,从目标点G 向起始点S 进行搜索,结果如图4(b)所示(FA THER 列表返回的路径记为pathnormal,有24 个节点),从图中可以看出,返回路径很好地绕过了凹形障碍。

图4 正向搜索Fig.4 Normal search

从图4 还可看出,返回路径是从右边绕过障碍的,这是因为目标点G 在起始点S 的右侧,导致了搜索点首先向右侧进行。若从左侧绕过障碍返回路径,可能会更短,那么如何实现向另一侧进行搜索呢?

这里采取的策略是从目标点G 向起始点S 进行逆向搜索。具体操作如下:先从目标点G 向起始点S 搜索一次,返回CLOSED 列表,返回路径如图5(a)所示;将CLOSED 列表中返回的节点看作可通过点,地图中的其他点都视为障碍点, 重新构建地图,再从起始点S 向目标点G 进行二次搜索,返回路径如图5(b)所示(FA THER 列表返回的路径记为path-converse,有14 个节点)。

图5 逆向搜索Fig.5 Converse search

比较path-normal(25 个节点)和path-converse(14 个节点),path-converse 的节点少,即为最后的优化路径。

总结上述的搜索策略,这里把它称为双向二次搜索,步骤如下:

1)正向搜索。从起始点向目标点(S →G)应用A*算法搜索一次,返回C LOSED 列表;将C LOSED表中返回的节点看作可通过点,地图中的其他点都视为障碍点,重新构建地图,从目标点向起始点(G→S)进行二次搜索,返回FA THER 列表,路径记为path-normal;

2)逆向搜索。从目标点向起始点(G →S)应用A*算法搜索一次,返回CLOSED 列表;将CLOSED表中返回的节点看作可通过点,地图中的其他点都视为障碍点,重新构建地图。从起始点向目标点(S→G)进行二次搜索,返回FA THER 列表,路径记为path-converse;

3)比较path-normal 和path-converse,择优取之(路径节点少的为优)。

值得说明的是,双向二次搜索策略是针对存在凹形障碍的地图提出的,对只有凸形障碍的地图同样适应(该种情况下一次搜索结果已经接近最短路径,二次搜索优化效果不明显)。实际应用中不必判断障碍物的形状,直接进行双向二次搜索即可得到最短路径。

4 结论

本文针对月球车全局路径规划的应用要求,对传统的A*算法流程进行了改进,减少了其时间和空间复杂度,使之在路径规划中的应用更加高效。同时对于存在凹形障碍的地图,给出了成功进行路径规划的处理方法;然后采用双向二次搜索策略对规划路径进行优化,避免路径掉入凹洞陷阱,达到输出最短路径的目的。该方法可以应用于月球车的全局路径规划。

目前的研究都是基于环境信息完全已知的情况,进一步将基于环境信息不完整的条件下进行路径规划,使算法应具有接收新的感知信息进行路径修正的能力。

)

[1]贾阳, 陈建新, 张熇.月球车关键技术分析[J].航天器工程, 2006, 3(9):16-22

[2]陈圣群, 滕忠坚, 洪亲, 等.A*算法在车辆导航系统中的应用研究[J].微计算机信息, 2008, 24(11-3):269-270, 303

[3]张海涛, 程荫杭.基于A*算法的全局路径搜索[J].微计算机信息, 2007, 23(6-2):238-239

[4]岳靓亮.基于Dijkstra、A*算法的汽车导航算路实现[D].长春:吉林大学, 2006, 5

[5]常晓飞, 段丽娟, 符文星,等.基于A*算法的无人机爬升轨迹设计[J].飞行力学, 2008, 26(6):22-25

[6]Ferguson D, Stentz A.The field D*algorithm for improved path planning and replanning in uniform and non-uniform cost environments[R].CM U Technical Report, CM U-TR-RI-05-19, 2005

[7]郝向荣.在智能搜索中A*算法的应用与研究[D].西安:西安建筑科技大学, 2007, 4

[8](美)Nils J.Nilsson 著.人工智能[M].郑扣根, 庄越挺, 译.北京:机械工业出版社, 2007:84-88

[9]姚雪梅.人工智能中A*算法的程序实现——八数码问题的演示程序[J].电脑与信息技术, 2002(2):1-3

[10]Lester P.A*pathfinding for beginners[EB/OL].[2009-08-31].http://w ww .gamedev.net.(2005-07-20)

[11]Al Hasan S, Vachtsevans G.Intelligent route planning for fast autonomous vehicles operating in a large natural terrain [J].Robotics and Autonomous System s,2002, 40(2):1-24