基于有限元法的桥梁结构稳定性分析
王玉山,闫 琴,金 瑾
(石河子大学水利建筑工程学院,石河子 832003)
基于有限元法的桥梁结构稳定性分析
王玉山,闫 琴,金 瑾
(石河子大学水利建筑工程学院,石河子 832003)
为探讨桥梁结构稳定性分析的方法,以二节点平面杆单元为例,采用有限元法推导了桥梁结构稳定问题的单元刚度矩阵,利用所得单元刚度矩阵和FORTRAN语言编制了有限元分析程序,然后对一门式桥墩中墩的结构稳定性进行了分析,并将临界荷载与欧拉公式及ANSYS所得结果进行了比较,从而验证了该单元刚度矩阵和该有限元法的正确性。
桥梁;结构稳定性;有限元法
桥梁结构特别是桥墩结构的稳定问题是关系到桥梁安全与经济的主要问题之一,它与桥梁结构的强度问题不同,主要是求出外荷载与结构内部抵抗力间的不稳定平衡状态,即变形开始急剧增长的状态,从而设法避免结构进入该状态。现今,大力新建的桥梁结构广泛采用高强度材料和薄壁结构及桥墩的高耸化,使得桥梁结构的稳定问题比以往更加突出,而国内外研究结构稳定问题常用的方法,如欧拉方法、能量法及振动法等都不能很好地解释桥梁结构的失稳现象。随着计算机技术和有限元法的不断发展,国内外学者[1~4]采用有限元法分析桥梁结构的稳定问题已很广泛,因此,采用有限元法近似分析桥梁结构的稳定性已成为一种趋势。
1 桥梁结构稳定问题的有限元分析
1.1 单元的位移模式及应变
以二节点平面杆单元为例,其中,每个节点考虑3个自由度(u,υ,θ),节点位移如图1所示。
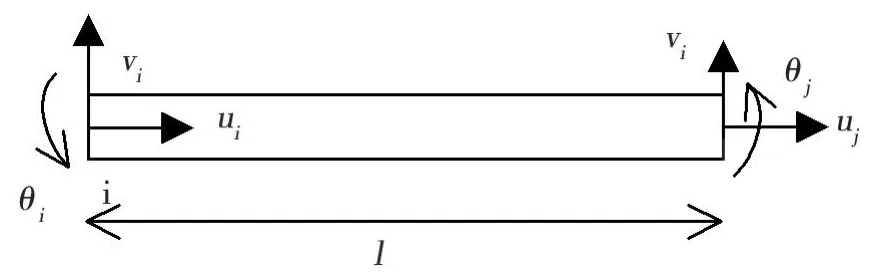
图1 二节点平面杆单元Fig.1 Two node 2-D bar element
利用竖向位移与转角的微分关系并考虑位移模式的完备性及协调性,单元内任一点位移 u,υ,θ,可通过型函数插值表示为[5~7]:

当不考虑剪切作用时,单元内任一点的正应变可表示为:

式(2)中,第1项表示轴向力引起的应变,第2项表示弯矩引起的应变,第3项表示杆的弯曲变形引起的应变。在通常的结构分析中,均略去第3项,但在稳定分析中,它反映了结构不稳定的因素,所以必须考虑。
1.2 单元的应变能及外力势能
单元的应变能可以表示为[8]:

设轴力以拉为正,整理可得

若单元有节点力 Pe作用,则节点力产生的外力势能可表示为

1.3 平衡方程的建立

式(7)中,Ke=为单元的弹性刚度矩阵,为单元的几何刚度矩阵,具体形式如下:

以上即为二节点平面杆单元在局部坐标系下的刚度矩阵和等效节点荷载向量。对于整体系下的刚度矩阵和等效节点荷载向量,可先利用坐标转换矩阵  ̄Ke=TTKeT和 ¯Pe=TTPe求得单元在整体系下的刚度矩阵和节点荷载向量,其中  ̄Ke为单元在整体系下的刚度矩阵,Ke为单元在局部系下的刚度矩阵,T为坐标转换矩阵。再通过对号入座的方法组装集成,则总体刚度矩阵及节点荷载向量,就可分别由所有的单元在整体系下的单元刚度矩阵和节点荷载向量组装集成为:
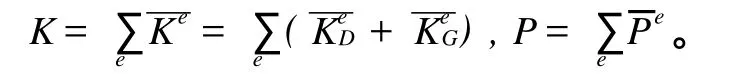
由式(7)知,如果结构所受外荷载不断增加,结构的节点位移也将不断增大,但由于结构的几何刚度矩阵与外荷载有关,因此这时结构的节点力和节点位移不再是线性的。设 Pe增大λ倍,则结构的轴力和几何刚度矩阵也都增大λ倍,故存在

若λ逐渐增大,使结构达到平衡的临界状态,则当δ变为δ+Δδ时,需满足式(8),即

由式(8)、(9)整理可以得到结构达到平衡临界状态的充分必要条件为

式(10)即为第一类结构稳定问题有限元计算的特征方程。若方程有 n阶,理论上方程存在 n个特征根,但在实际中只有最小的特征根才与结构失稳的临界荷载存在关系。假设最小的特征根为λcr,则结构失稳的临界荷载为λcrP,因此对结构稳定问题分析的关键可归结为对式(10)的求解。
2 算例及程序验证
采用FORTRAN语言,通过上述平面杆单元的弹性刚度矩阵和几何刚度矩阵编制了相应的稳定问题分析程序。为了验证本文所得单元刚度矩阵及分析程序所得结果的正确性,并与欧拉公式所得结果进行方便的比较,对图2所示门式桥墩一号墩的结构稳定性进行了算例分析。
一等截面门式桥墩有外力作用在1号墩顶部时(图1),确定该门式桥墩的临界荷载 Pcr。已知:弹性模量 E=20GPa,墩横截面尺寸 a=500mm。
计算分析中考虑该门式桥墩的墩底位移均被约束,墩顶所受约束在考虑盖梁的影响后,简化为铰接处理。程序中采用乘大数法对1号墩的刚度矩阵进行修正,然后按照本文的约束方法分别用本文、欧拉公式和ANSYS三种方法计算1号墩的临界荷载Pcr,其结果依次为2.273×103k N、2.328×103k N、2.351×103k N。与欧拉公式及ANSYS分析所得结果相比,由本文给出的单元刚度矩阵编制的分析程序所得结果符合较好,相对误差均小于5%。此外,本文的分析结果虽然略微偏小,但对于工程中的实际问题,由于施工误差以及材料不均匀性的影响,实际中临界荷载值也均小于理论值。

图2 门式桥墩Fig.2 Double-column bridge piers
4 结语
本文采用有限元法推导了二节点平面杆单元稳定性分析的单元刚度矩阵,并编制了相应的稳定性分析程序,然后用该程序对一门式桥墩中墩的稳定性进行了计算分析。通过与欧拉公式及ANSYS所得结果的比较,验证了该单元刚度矩阵及分析程序的正确性,虽然所得结果与欧拉公式ANSYS分析所得的结果存在一定的差异,但从实际考虑,它仍可以作为桥梁结构稳定性分析的一个重要参考值。
[1]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001.
[2]朱向前.高墩稳定问题的求解方法及应用[J].公路交通技术,2008,(3):59-63.
[3]唐承平.大跨连续钢构桥高墩稳定问题研究现状[J].四川建筑科学研究,2008,34(6):68-70.
[4]吕东莉.系杆拱桥一类稳定问题的探讨[J].现代交通技术,2006,(1):47-50.
[5]王勖成,邵 敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997.
[6]王元汉,李丽娟,李银平.有限元法基础与程序设计[M].广州:华南理工大学出版社,2001.
[7]贺栓海.桥梁结构理论与计算方法[M].北京:人民交通出版社,2003.
[8]蔺鹏臻,刘世忠.桥梁结构有限元分析[M].北京:科学出版社,2008.
[9]谢祚水.计算结构力学[M].武汉:华中科技大学出版社,2004.
[10]江见鲸,贺小岗,傅德炫.建筑结构分析程序[M].北京:中国建筑工业出版,1993.
Analysis of Bridge Structure Stability Based on the Finite Element Method
WANG Yushan,YAN Qin,JIN Jin
(College of Water Conservancy and Architectural Engineering,Shihezi University,Shihezi 832003,China)
The element stiffness matrix of bridge structure stability was deduced by using the finite element method,which was based on two node 2-D bar element.An analysis procedure of the finite element was developed by using the element stiffness matrix and language of FORTRAN for the stability of piers.At last,the element stiffness matrix and the analysis procedure were verified by comparing the piers analysis result with result of ANSYS and Euler equation.
bridge;structure stability;the finite element method
TU311.2;U441
A
1007-7383(2010)01-0106-03
2009-09-16
王玉山(1979-),讲师,从事桥梁工程应用研究;e-mail:wysbgxn@shzu.edu.cn。

