考虑流量误差的B样条压力反褶积模型及其应用

胡小虎,郑世毅,2

(1.中国石油大学石油工程学院,北京 102249;2.Heriot-WattUniversity,Edinburgh EH144AS,UK)

考虑流量误差的B样条压力反褶积模型及其应用

胡小虎1,郑世毅1,2

(1.中国石油大学石油工程学院,北京 102249;2.Heriot-WattUniversity,Edinburgh EH144AS,UK)

在二阶B样条的基础上,推导出考虑流量测量误差的压力反褶积模型,提出各流动期真实流量的确定方法,并利用模型预测真实流量获得对应的真实压力响应。结果表明,流量误差为 10%时,利用本模型获得的压力响应与在没有流量误差下的压力响应结果一致,远优于 ILK模型的结果。这说明所提出的压力反褶积模型可以有效消除流量误差对压力响应结果带来的影响。

油田开发;油田动态;B样条;压力反褶积;流量误差;流量校正

试井技术中压力导数法以及随后提出的各种油藏模型,极大地丰富和完善了现代试井方法[1-3]。当前,随着永久式井下压力计 (PDG)技术在新开发油田的使用,持续的井底压力监测已经成为一种趋势[4]。利用 PDG数据,不仅可以降低直接试井带来的成本增加,而且可以扩大油藏探测范围,实现对油藏的实时监测管理。然而,传统的压力导数法只能对单个流动期进行分析,不能充分利用 PDG数据获取不同流动期内包含的油藏探测范围信息,而使用迭加原理或时间函数对多流动期数据分析也会存在问题[5]。利用反褶积方法可以避免上述问题,获得油藏在全部时间范围内、单位流量下的油藏压力响应,是解释 PDG数据的一种重要方法[6-12],但后来von Schroeter[9],Levitan[11-12]等的研究才解决了该方法的稳定性问题,并使其得到实质性的进展及工业应用。 ILK等[13-14]提出的基于二阶 B样条的压力反褶积方法也是一种重要的反褶积方法,但由于采用Laplace变换形式来计算超定方程的系数矩阵,因此没有考虑流量测量误差,而流量误差对压力反褶积结果具有重要影响,Baygün等[15]的模型正是由于没有考虑流量测量误差,导致流量误差大于 1%时模型无法使用[9]。为此,笔者在 ILK的二阶 B样条方法的基础上,建立考虑流量误差的压力反褶积模型,并提出各流动期真实流量的确定方法。

1 数学模型及求解

1.1 数学模型

对于线性系统,变流量对应的井底流压可以使用 Duhamel积分[16]表示为

根据 I LK等[13-14]的研究,压力响应可以通过在对数分布的节点上采用二阶 B样条的线性组合表示,即

由于需要考虑流量测量误差,因此必须将各流动期的流量表示成向量形式来求解。当时间划分的足够细的情况下,任何流量变化形式都可以使用阶梯形变化的流量来表示,而阶梯形变化的流量可以使用 Heaviside函数来表示,即

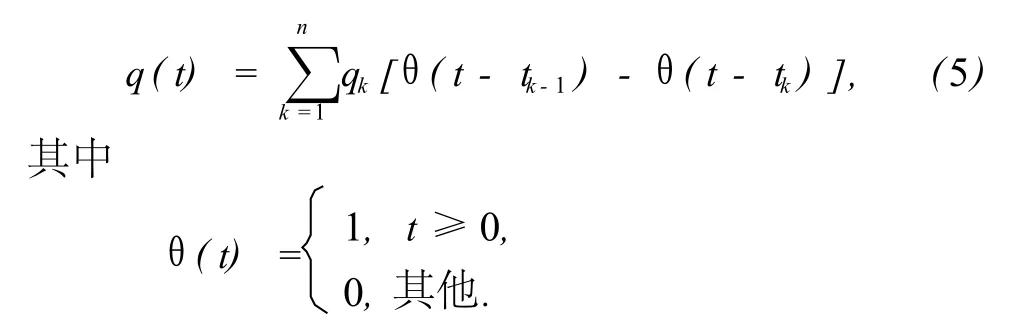
由于地面流量数据中含有测量误差,为了能消除由式 (1)得到的压力响应中流量误差的影响,需要将各流动期的测试流量用真实流量来代替。为此,将各流动期的真实流量 qk,mdtrue表示为测试流量 qk与相应校正系数αk的乘积,则测量流量可以表示为

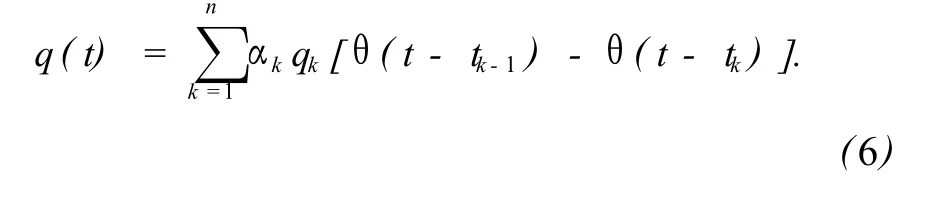
对应的真实流量可以表示为

式 (9)中的系数矩阵Mijk是个三维系数矩阵,可以根据式 (9)定义在实空间通过离散方式求解,也可根据 Laplace变换的线性原则,将式 (9)变换到Laplace空间求得相应的系数矩阵后,数值反演到实空间得到相应的系数矩阵。本文采用前一种方法求解。

1.2 模型求解

式(10)需要建立相应的目标函数,通过最小化来求最优解。建立的目标函数如下式所示:

式中,ωi为约束对应的观测值;Ωi为约束对应的模型预测值;si为约束对应的误差阀值,约束类型包括压力约束、流量约束以及压力响应导数曲线光滑度约束;N1为压力约束个数;N2为流量约束个数;N3为光滑度约束个数。压力约束选择的 si为 0.06 kPa,光滑度约束选择的 si为 0.05。对于流量约束,在分析中发现,本文模型中的流量误差阀值 si只影响结果曲线在双对数诊断图上的上下平移,因此,本文中统一取流量单位为 1。光滑度约束是在所有的 B样条节点及相邻两节点的中点之间来检查。

在求解出 c和α向量后,压力响应可以通过下式求得:

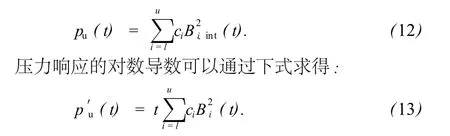
2 结果分析

2.1 流量误差对 I LK模型的影响

为了说明 I LK模型不考虑流量测量误差对压力反褶积得到的压力响应结果的影响,本文中首先以圆形封闭均质油藏来展开分析。测试使用的流量 -压力史数据见图 1。模拟使用的主要参数如下:井眼内半径为 0.09144 m,井储系数为 0.034 m3/MPa,储层厚度为 9.144 m,孔隙度为 0.1,表皮系数为 2,黏度为 1 mPa·s,渗透率为 10×10-3μm2,综合压缩系数为 4.35×10-4MPa-1,油藏外半径 600 m,原始地层压力为 34.474 MPa。流量误差为 3%和 5%时对压力响应结果的影响见图 2。从图 2可以明显看出,流量误差对早期的压力响应几乎看不出影响,但对于从径向流向拟稳态流过渡,流量误差对压力响应结果影响非常明显。当模拟稳态流动对应的测试数据时间不足时,会影响到边界类型的判断及参数解释。

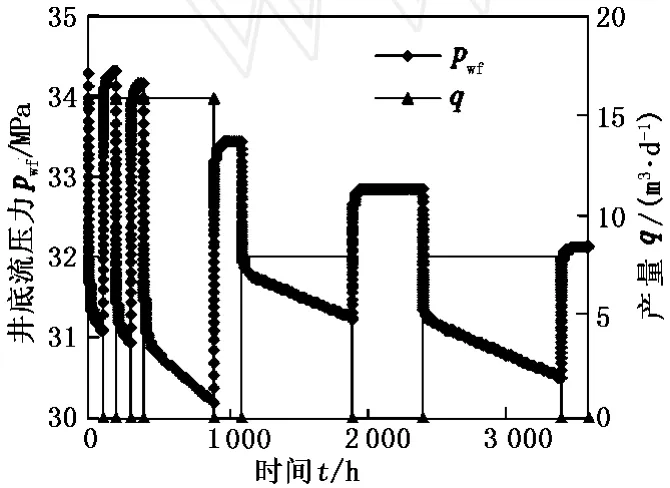
图 1 模拟使用的流量史及压力史数据Fig.1 S imulated rate and wellbore flowing pressure history

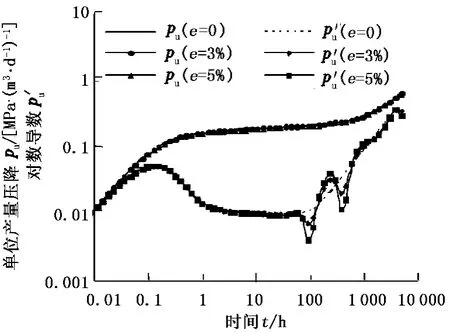
图 2 流量测量误差为 3%和 5%时对 ILK模型压力响应结果的影响Fig.2 I mpact of 3%,5%rate errors on deconvolved pressure response by I LK model

从对 I LK模型的分析可以看出,由于没有考虑流量测量误差,导致得到的压力响应导数曲线中由径向流向拟稳态流的过渡段及拟稳态流对应直线段的结果异常,并且无法通过光滑度约束来消除。因此,在压力反褶积模型中必须考虑流量测量误差。

2.2 流量误差对本文模型的影响

为了说明本文模型在处理流量误差方面相对于I

LK模型的优越性,分析了流量测量误差对由本文模型得到的压力响应结果的影响。对于本文模型,当给定压力和流量测试数据,并由式 (11)求出最优的c和α解后,就可以根据式 (12)和式 (13)来求解压力响应和压力响应导数。

对于圆形均质封闭油藏,图3中给出了在5%和10%流量测量误差下,由本模型得到的压力响应与没有流量误差下的压力响应结果。在双对数图上可以看出,含流量误差的压力数据经本文模型反褶积算法处理后,得到的压力响应结果与没有流量误差下的压力响应结果之间具有相同的油藏模型特征,只是曲线位置发生了上下平移。

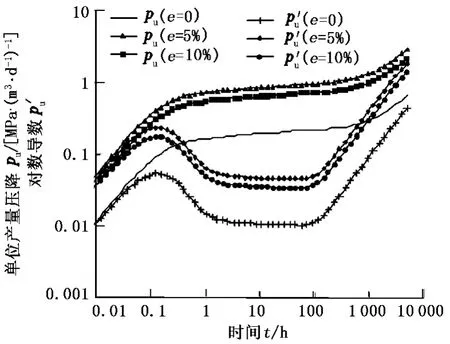
图 3 流量测量误差为 5%和 10%时本文模型得到的压力响应曲线Fig.3 Comparison analysis of impact of 5%,10%rate errors on deconvolved pressure response by proposed algorithm

2.3 真实流量的确定方法

在根据式 (11)求解得到α向量后,由式 (7)就可以计算得到各流动期的模型预测流量 qi,mdtrue。分析了预测流量与各流动期的真实流量之间的关系,结果见图 4。从图中可以看出,流量误差为 5%和10%时,除了压力恢复期外,所有模型预测的流量与相应真实流量之间的比值分别是完全相同的。将模型预测流量 qi,mdtrue与真实流量 qi,real之间的比例系数记为

此规律可以用来解释由本模型得到的压力响应曲线与真实压力响应曲线之间的关系:由于在最优化过程中,得到的各流动期的模型预测流量与相应真实流量之间都只相差一个共同的比例系数β,相当于将真实流量放大或缩小相同比例后得到的压力响应。因此,与真实压力响应相比,本模型得到的压力响应形状相同但发生了上下平移。

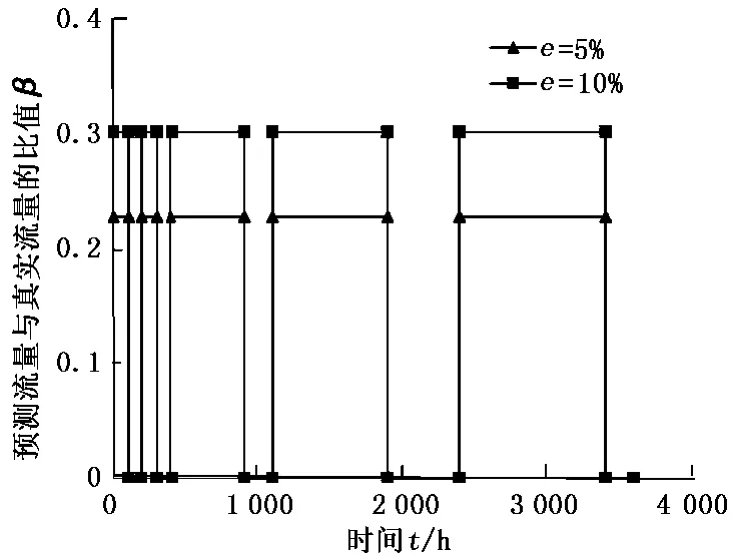
图 4 流量误差为 5%和 10%时由本模型确定的各流动期模型预测流量与真实流量的比值Fig.4 Ratios of predicted rates to true values for 5%,10%rate errors

由于得到的各流动期模型预测流量与真实流量之间只相差一个相同的比例系数,因此在知道累积产量或某个流动期的准确流量后,就可以通过式(6)确定出系数β,从而其他流动期的真实流量就可以由式 (14)来确定。由于累积产量数据一般现场都可以获取,并且相对较为准确,因此可以根据累积产量数据求解得到系数β,代入式 (14)后就可求出各流动期的真实产量。

在没有累积产量等可利用数据的情况下,可以根据最小化原则由下式来确定各流动期的真实流量:

其中,qmeas,i为 i流动期的测量流量,qi,mdtrue为通过式(8)确定的 i流动期模型预测流量。式 (15)中,为了避免高流量数据在目标函数中的权重远高于低流量数据的权重,采用预测流量与真实流量之间的相对比值来建立目标函数。

针对图 3算例中流量测量误差 10%的情况,分析了由式(15)确定的各流动期的模型预测流量与相应真实流量之间的关系,结果见表 1。从表中可以看出,在流量测量误差为 10%时,模型预测的各流动期流量的相对误差约为 0.1%。由此可以看出,经此处理后,可以大大减小流量数据中的不确定性。

上述流程可以反复,一般两次左右后,得到的β系数接近于 1,此时的模型预测流量与真实流量几乎一致。

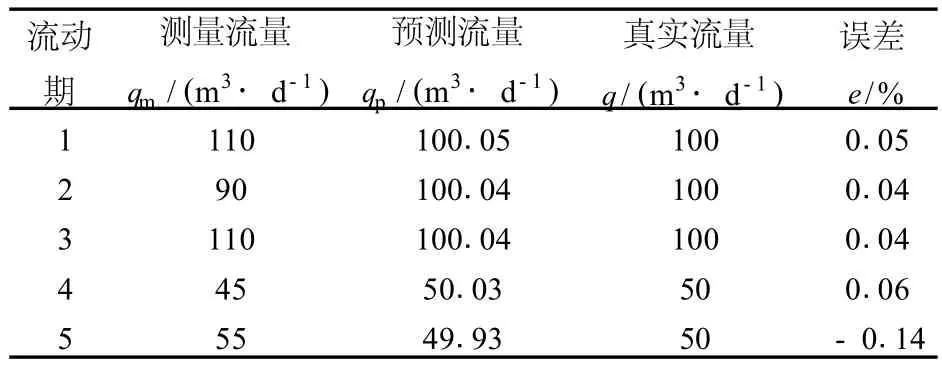
表 1 由本文模型预测的各流动期流量误差Table 1 Error for predicted rates for each following period by proposed algorithm

2.4 真实压力响应的确定

确定出各流动期的真实流量后,可以使用此真实流量代替原始的流量测试数据,输入本模型或 ILK模型,得到压力、流量数据对应的真实压力响应。

针对圆形封闭均质油藏,分别比较了流量误差为 5%及 10%时,经本模型处理后得到的油藏压力响应与没有流量误差下获得的真实压力响应,结果见图 5。从此对比图中可以看出,使用本模型获得的压力响应与真实压力响应完全一致。

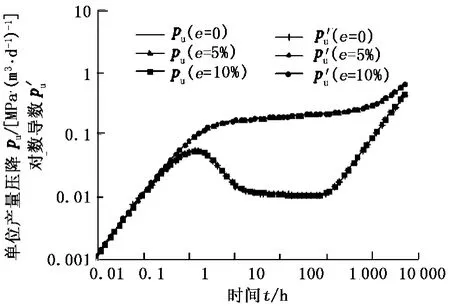
图 5 流量误差为 5%和 10%时由本文模型获得的真实压力响应对比Fig.5 Comparisons of pressure response deconvolved with true results for 5%,10%rate errors by proposed algorithm

3 结 论

(1)流量误差会影响 ILK模型压力反褶积得到的压力响应结果。

(2)利用本文提出的模型,可以综合利用其他生产数据来准确确定各流动期的真实流量,在流量误差为 10%时计算得到的真实流量相对误差约为0.1%。

(3)利用本文模型对含流量误差 5%和 10%的测试数据反褶积处理后,确定出的压力响应与真实压力响应一致,说明建立在二阶 B样条基础上的压力反褶积模型可以有效消除流量误差对压力响应结果带来的影响。

[1] STAN ISLAVE J F,卡比尔 C S.压力不稳定试井分析[M].谢兴礼,陈钦雷,译.北京:石油工业出版社,1996.

[2] 林加恩.实用试井分析方法[M].北京:石油工业出版社,1996.

[3] 卢唐德.试井分析理论及方法[M].北京:石油工业出版社,1998.

[4] GR INGARTEN A C,ROLFSVAAG T,BRUNER J.Use of downhole per menent pressure gauge data to diagnose production problems in a north sea horitontal well[R].SPE 84470,2003.

[5] ZHENG Shiyi,STE WART G,CORBETT P.Analyzing pressure transient test in semi-Infinite and finite reservoirs using de-superposition method[R].SPE 64753-MS,2000.

[6] CHENG Y M,LEE W J,MCVAY D A.Fast-fouriertransform-based deconvolution for interpretation of pressure-transient-test data dominated by wellbore storage[R].SPE 84471,2005.

[7] LLKD,ANDERSON D M,VALKO P P,et al.Analysis of gas-well reservoir performance data using B-spline deconvolution[R].SPE 100573,2006.

[8] ZHENG S Y,WANG F.Application of deconvolution and decline-curve analysismethods for transientpressure analysis[R].SPE 113323,2008.

[9] SCHROETER T V,GR INGARTEN A C.Deconvolution ofwell test data as a nonlinear total least squares problem[R].SPE 71574,2001.

[10] SCHROETER T V,HOLLAENDER F,GR INGARTEN A C.Analysisofwell test data from permanent downhole guages by deconvolution[R].SPE 77688,2002.

[11] LEV ITAN M.Practical applications of pressure/rate deconvolution to analysis of real well tests[R]. SPE 84290,2003.

[12] LEV ITAN M,CRAWFORD G E,HARDW ICKA.Practical considerations for pressure-rate deconvolution of well-test data[R].SPE 90680,2004.

[13] LLKD,BLAS INGAME TA.Deconvolution of variablerate reservior-performance data using B-splines[R].SPE 95571,2005.

[14] ONURM,C INARM,LLKD,et al.An investigation of recent deconvolution methods for well-test data analysis[R].SPE 102575,2008.

[15] BAYGÜN B,KUCHUK F J,AR IKAN O.Deconvolution under normalized autocorrelation constraints[R].SPE 28405,1997.

[16] van EVERD INGEN A F,HURSTW.The application of the Laplace transfor mation to flow problems in reserviors[J].Trans,A IME,1949,16:305-324.

A new B-splines pressure deconvolution algorithm considering rate measurement errors and its application

HU Xiao-hu1,ZHENG Shi-yi1,2
(1.College of Petroleum Engineering in China Petroleum University,Beijing102249,China;2.Heriot-W att University,Edinburgh EH144AS,UK)

A new algorithm based onB-splineswasproposed to consider the ratemeasurement error during pressure deconvolution.Severalmethodswere provided to determine the actual rates for each flow period,which can be utilized to determine the actual pressure response in turn.The results show that unit-rate pressure response with 10%rate error agrees wellwith the true results,which ismuch better than that from ILKmodel.The new algorithm can overcome the effect of rate measurement error on the pressure response.

oilfield development;oilfield perfor mance;B-splines;pressure deconvolution;rate measurement error;rate correction

TE 331

A >

10.3969/j.issn.1673-5005.2010.06.015

1673-5005(2010)06-0080-05

2010-02-05

国家重大专项课题 (20085024-002)2009JY001

胡小虎 (1974-),男 (汉族),安徽池州人,博士研究生,主要从事油气田开发方面的研究。

(编辑 修荣荣)