浅谈数学探究学习

黄娟娟

探究学习即从学科领域或实现社会生活中选择和确定研究主题,在教学中创设一种类似于科学研究的情境,通过学生自主、独立地发现问题、实验、操作、调查、信息搜集与处理、表达与交流等探索活动,获得知识、技能、情感与态度的发展.

一、探究学习的实施.

笔者在教学中发现教材中很多内容可以实施探究学习,探究学习可以运用于课堂的某一部分,也可以贯穿于课堂始终在具体的教学实践中,要根据实际情况选择合适的方法进行有效的探究学习.

1抛出问题,创设探究学习的氛围.

数学源于问题,问题是思维的起点,任何有效的数学教学必须以问题为起点,以问题为驱动,激发学生的欲望在教“勾股定理”时,我选择了下列问题情境.

情境1 一次强台风中,一根旗杆在离地面9m处折断倒下,旗杆顶部落在离旗杆底部12m处,旗杆折断之前有多高?.

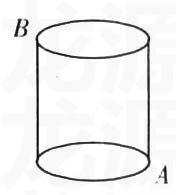
情境2 如图,圆柱高30cm,底面直径10cm,一只蚂蚁沿着圆柱侧面从下底面的A处爬到上底面的B处,它怎么爬最近,最近距离是多少?.

情境1简单,学生易于理解,可以较快的切入教学主题情境2具有一定的趣味性,可以激发学生的学习兴趣,但更具挑战性.

2学生大胆尝试,猜想解决问题.

为了探索出直角三角形三边的关系,可设计如下活动:在纸上任意画出若干个直角三角形,测量它们各边的长度,猜想并检验三边长度之间的关系条件允许的话可以利用几何画板让学生自主地进行探究和猜想,进而排除错误猜想,验证正确猜想在探索中,学生往往会先思考三边长度之间的一次关系,而较难想到三边长度之间的二次关系可以在学生发现未必存在一次关系的基础上,提醒它们之间是否存在二次关系.

3合作交流,完成探究.

在教学中,通过创设问题情境,合作小组内自主探索、交流、对话,获得成效小组之间互相交流、评价,达到教学互动、互促,形成比、学、赶、帮的学习氛围,从而使学生在合作交流的过程中学会与他人合作,并能与他人交流思维的过程和结果,体会在解决问题过程中与他人合作的重要性,感受获得成功的喜悦.

例如,在圆与圆的位置关系的教学中,我先让学生通过自主探究得到在五种不同位置下圆心距和两圆半径之间的大小关系,发现部分学生在两圆相交、内切、内含下得出圆心距都是小于两圆半径之和的结论,此时让学生互相交流讨论,这样学生就发现了自己的错误之处,再结合几何画板的测量演示功能,共同得出正确的结论.

4应用巩固.

通过探究获得有关命题后,要将其在一定的应用情境中加以巩固为此,可以让学生回过头来解决原来情境中的问题,与前面形成呼应,使整个课堂成为一个有机的整体;当然,如果因为时间关系或者初始问题比较难,也可以另外设计一些习题.

二、适宜探究学习的内容.

1对定理法则的探究.

在定理、法则的发现中进行探究性学习前人的知识对学生来说是全新的,学习应是一个再发现、再创造的过程教师要引导学生置身于问题情境中,揭示知识背景,从数学家的废纸篓里寻找探究痕迹,让学生体验数学家们对一个新问题是如何去研究、去创造的,暴露思维过程,体验探索的真谛.

例如,在三角形中位线知识的教学中,笔者发现,对于三角形中位线性质的证明,由于新旧知识间的距离较大,大多数学生都无法独立完成证明过程因此,尝试通过“把一个三角形剪一刀拼成一个平行四边形”的操作活动,铺设恰当的认知阶梯,让学生在活动中体验并概括三角形中位线的概念.

问题1 如图,是一个任意的三角形,请在三角形上剪一刀,使得分成的两块正好拼成一个平行四边形.

问题2 若图中我们剪下的位置称为三角形的中位线,你能给出三角形中位线的定义吗?一个三角形有几条中位线?.

问题3 通过活动和观察,你能发现中位线和三角形的第三边有什么位置和数量关系?用量角器和刻度尺进一步验证你的猜想.

问题4 能否对你的猜想进行证明?.

2数量关系、变化规律的探究.

代数中的很多内容充满了用来表达各种数学规律的模型,如代数式、方程、函数、不等式等,教师要引导学生进行观察、实验、猜测、验证、推理与交流等数学活动,探索事物的数量关系、变化规律.

3对实际问题的探究.

数学问题在实际应用的探究中,教师应尽可能多地提供一些现代生活中学生感兴趣的事例进行探究例如,市场销售问题、办厂赢亏测算、股票风险投资、贷款利息计算、道路交通状况、环境资源调查、有奖销售讨论、体育比赛研究等等这些素材可从报刊杂志、计算机网络中查找学习了函数和不等式的知识后,可以让学生计算有关的经济问题.