用《几何画板》进行数学新课程教学

郭平均

随着信息技术在教育教学领域中的广泛应用,教学理念、教学内容、教学方式、教学环境等各个方面也随之发生了重大的变革。在新课程标准中,提出了“把现代信息技术作为学生学习数学和解决问题的强有力的工具”,要利用现代教育技术对数学课程领域采取了“大力开发”的策略,致力于改变学生的学习方式,使学生乐意并有更多的精力投入到探索性的数学活动中。

《几何画板》作为“动态黑板”为我们创设了一个数学实验室,提供了一个理想的做数学的环境,学生可以从“听”数学转变到“做”数学。

一、利用几何画板让学生动手操作,培养其自学能力、解决问题的能力

利用几何画板其动态性和形象性,可以给学生创造一个实际“操作”几何图形的环境。学生可以任意拖动图形、观察图形、猜测并验证,在观察、探索、发现的过程中增加对各种图形的感性认识,形成丰厚的几何经验背景,从而更有助于学生理解和证明。

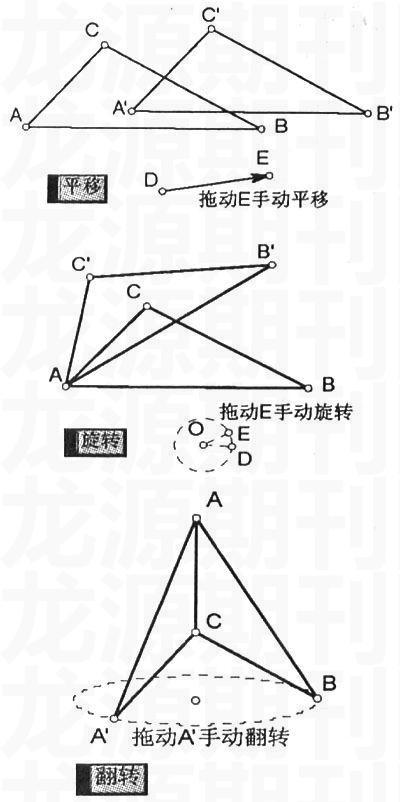
例1:图形的全等变换:

通过动画控制按钮或拖动点进行图形的平移、旋转、翻转的变化,使学生从难以绘制的图形中感受全等图形“变换”的动感,学生从中去寻求到问题解决的方法和依据,并从中去认清全等证明变换的本质。

二、数形结合化抽象为直观,在培养观察力中训练创造性思维

华罗庚说:“数缺形少直观,形缺数难入微”。函数的两种表达方式:解析式和函数图象之间常常需要对照。

例2:二次函数的系数特性和平移规律。

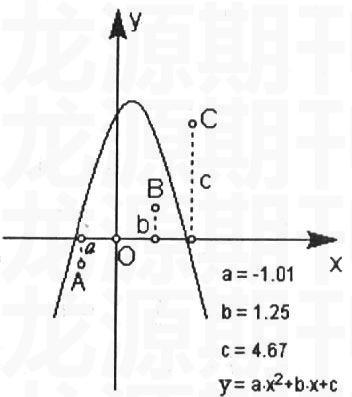
利用《几何画板》演示,引导学生思考。对于二次函数y=ax2+bx+c拖动屏幕上A、B、C三点,a、b、c的值随之改变,探求y=ax2+bx+c的开口大小、开口方向、对称轴、顶点坐标、与x轴的交点个数与系数a、b、c的关系及函数的增减性与对称轴的关系。

三、结合实际生活情景,进行动画模拟、猜想、验证结论,解决动态最值问题

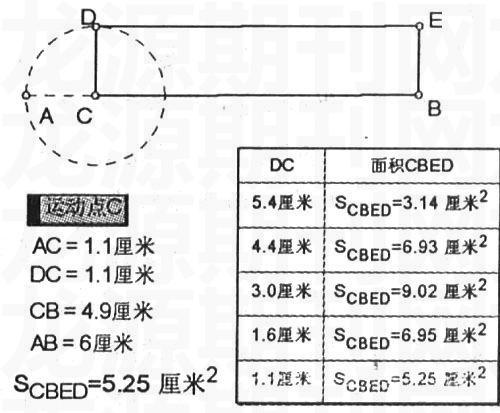
例2:一条长为12cm的绳子围成一个长方形,当宽为多少时其面积最大?

教师作线段AB=6cm,AB上去一点C,通过控制按钮改变点C的位置,利用几何画板的制表功能,求出一系列面积,然后让学生观察动画、猜想结论,再利用数学知识进行严密的证明,从而使有些在传统教学中显得枯燥和乏味的教学内容,引入“几何画板”后,许多内容变静为动,学生在“动”中求知,激发了学生的学习兴趣与学习积极性。

四、构建实验平台,模拟数学实验,营造“猜想-实验-发现-验证”的研究环境

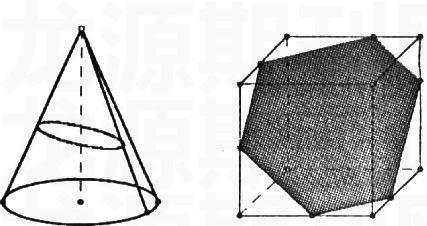
学习任何知识最好的途径是自己去发现,不仅营造“猜想-实验-发现-验证”的研究环境,而且更有利于教师关注学生的体验、情感和实验过程,体现“以学生发展为本”的教学理念,通过数学实验,可以增进学生之间的合作

交流,加深对数学问题的理解。比如正方体、圆锥的截面,

几何体的三视图等等,通过用几何画板制作的动画能起到很好的效果。

五、提高兴趣、培养图案设计能力、审美能力

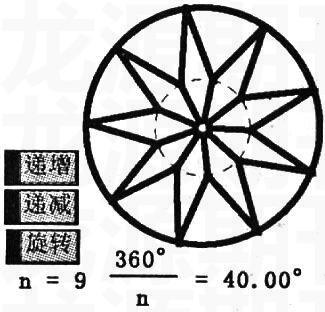
丰富多彩的“动画”模型,给学生一种耳目一新的视觉享受,从而让学生充分想象,提高想象力。利用《几何画板》制作旋转的多角星,并用变换中的迭代工具能控制角星的个数,色彩鲜艳、动态直观的画面演示设计“轴对称”、“中心对称”角星图案,学生易总结当奇数角星仅为轴对称图形,而偶数角星时,既为轴对称图形又为中心对称图形,真切地感受图形变换的乐趣和价值。课后提出利用“轴对称”、“中心对称”等知识进行设计图案的实践活动,能更好地认识自己的生活空间,充分调动学生积极性和参与热情的前提下可以充分发挥学生的主动性和创造性,更有助于培养学生的创新精神。

总之利用《几何画板》软件来探索有关数学的知识,把多媒体辅助数学教学从目前的演示型为主向互动型转化,真正实现学生自己对知识的建构,使学生体会到“做数学”的思想。通过自己的亲身实践,找到问题的解决方法,并在问题解决过程中理解和掌握抽象的概念和原理,获得真正的数学体验,从而让学生真正体会到“做数学”的乐趣。