含多个参数的Josephus问题递归关系研究

赵天玉，王安平 (长江大学信息与数学学院，湖北 荆州 434023)

严 政 长江大学信息与数学学院，湖北 荆州 434023 应用数学湖北省重点实验室(湖北大学)，湖北 武汉 430062

含多个参数的Josephus问题递归关系研究

赵天玉，王安平 (长江大学信息与数学学院，湖北 荆州 434023)

严 政 长江大学信息与数学学院，湖北 荆州 434023 应用数学湖北省重点实验室(湖北大学)，湖北 武汉 430062

Josephus问题是一个古老的问题，对Josephus问题进行变形，可以得到一类递归关系。对这类递归关系进行了推广，得到一类含多个参数的递归关系模型，讨论了这类递归关系模型的求解方法，并采用d-进制记数法给出了这类递归关系模型的解。

Josephus问题；递归关系；模型；d-进制记数法

1 Josephus问题

Josephus问题[1]是一个古老的问题，在组合数学、题库组卷及数列生成[2,3]中都涉及此问题。它是以1世纪著名历史学家Flavius Josephus命名的。据传说，在犹太人和古罗马人战争期间，Josephus是陷入罗马人陷阱的41个犹太反抗者之一。反抗者宁死不做俘虏，他们决定围成一个圆圈，且环绕圆圈来进行，杀死所有第3个剩下的人，直到最后一个人自杀为止。但是Josephus和一个不告发的同谋者感到自杀是愚蠢的行为，所以他以自己的数学才能，快速计算出在此恶性循环中他和他的朋友该站的地方，活着逃出了陷阱。若Josephus是最后一位幸存者，他应该站的地方编号J(41)是多少？

文献[2]给出了一般的Josephus问题及其算法，文献[3]对几种求解此问题的算法进行了比较，文献[1]对Josephus问题进行了变形，从围着一个圆的编号为1到n的n个人开始，排除所有第2个剩下的人，直到最后仅仅剩下1个幸存者为止，得到下列递归关系模型：

J(1)=1J(2n)=2J(n)-1(n≥1)J(2n+1)=2J(n)+1(n≥1)

(1)

并给出了模型(1)的解。若自然数n用二进制表示为n=(bm,bm-1,…,b1,b0)2，这里bm=1，则：

J(n)=J((bm,bm-1,…,b1,b0)2)=(bm-1,bm-2,b1,b0,bm)2

下面，笔者对递归关系模型(1)进行了推广，得到一类含多个参数的递归关系，并讨论了这类递归关系的求解方法*应用数学湖北省重点实验室开放基金资助项目。。

2 Josephus问题递归关系的推广

对Josephus问题进行变形所得模型(1)进行推广，得到一般递归关系模型：

J(j)=αj(1≤jlt;d)

(2)

J(dn+j)=cJ(n)+γjn+βj(0≤jlt;d,n≥1)

(3)

式中，c,d,αj(j=1,2,…,d-1),βj,γj(j=0,1,…,d-1)都是常数，其中c,d是正整数，且c≥1,d≥2。

3 含多个参数的递推关系的求解

传统的求解递归关系的方法是特征根法[4]、母函数法与差分法[5]、迭代法与归纳法[6]。但针对递归关系模型的特殊性，笔者采用数的广义d进制表示方法求解模型。

设：

n=(bm,bm-1,…,b1,b0)d=bmdm+bm-1dm-1+…+b1d+b0bm≠0

称为n的广义d进制表示。特别地，当0≤bilt;d(i=0,1,2,…,m)时，实际上就是n的d进制表示。

利用n的d进制表示递归模型式(2)、式(3)可得：

=cmαbm+cm-1βbm-1+cm-2βbm-2+…+cβb1+βb0+cm-1γbm-1(bmd0)+cm-2γbm-2(bmd+bm-1d0)

+…+cγb1(bmdm-2+bm-1dm-3+…+b2d0)+γb0(bmdm-1+bm-1dm-2+…+b1d0)

即:

(5)

下面对参数取值的情况进行讨论。

(Ⅰ)当βj=γj=0(j=0,1,…,d-1)时，从式(4)可知递归模型的解为：

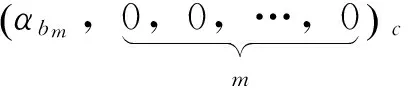
(Ⅱ)当γj=0(j=0,1,…,d-1)时，从式(4)可知递归模型的解为：

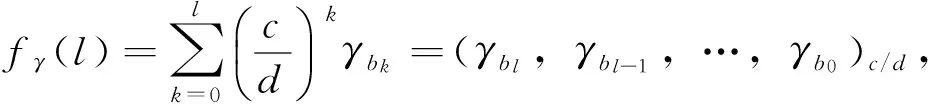
(Ⅳ)当c=d,γj=γ≠0(j=0,1,…,d-1)时，从式(5)可知递归模型的解为：

(Ⅴ)当c≠d,γj=γ≠0(j=0,1,…,d-1)时，从式(5)可知递归模型的解为：

(Ⅵ) 一般情况。采用(Ⅲ)的记号，从式(5)可知递归模型的解为：

J(n) =J((bm,bm-1,…,b1,b0)d)

4 解的另一种表示方法

设:

其中，n=(bm,bm-1,…,b1,b0)d(其中bm≠0)是n的d进制表示。那么系数Ai(n)(i=1,2,…,d-1)和Bi(n),Ci(n)(i=0,1,…,d-1)的表达式如何？

很显然，从式(5)可知，当i≠bm时，Ai(n)=0；Abm(n)=cm。

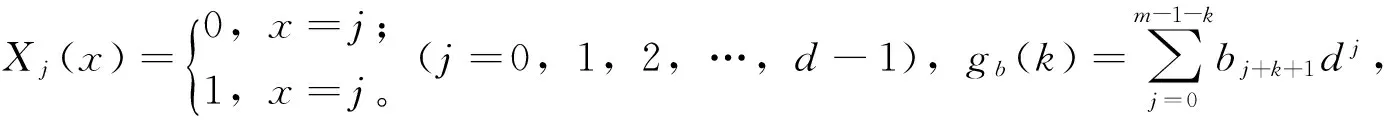
即：

故：

J(n) =J((bm,bm-1,…,b1,b0)d)

[1]格雷厄姆 R L，克努特 D E，帕塔希尼克 O.具体数学[M].庄心谷 译.西安：西安电子科技大学出版社，1992.7～14.

[2]陈海山，钱锋，田英，等.Josephus问题的算法设计与应用研究[J].计算机工程与应用，2007，43(1)：61～64.

[3]王永红.约瑟夫环经典问题的几种算法比较[J].现代计算机，2008，(1)：36～37.

[4]卢开澄，卢华明.组合数学[M].第3版.北京：清华大学出版社，2002.126～150.

[5]杨振生.组合数学及其算法[M].合肥：中国科学技术大学出版社，1997.106～135.

[6]孙世新，张先迪.组合原理及其应用[M].北京：国防工业出版社，2006.157～161.

[编辑] 洪云飞

O157

A

1673-1409(2009)02-N001-03

2009-02-12

赵天玉(1958-)，男，1981年大学毕业，硕士，教授，现主要从事组合数学方面的教学与研究工作。