偏最小二乘回归在运动训练研究中的应用

摘要:OLS逐步回归等变量删除法在处理运动训练领域的共线性数据时,会将一些重要的解释变量或样本点排除在模型之外,从而削弱了理论的优先地位和导向功能。PCR模型对系统信息的综合与筛选能力不佳,拟合与预测精度不甚理想。PLS对系统信息的综合与筛选能力强、拟合与预测精度较高,是目前处理运动训练领域小样本多指标共线性数据的一个非常有效的统计方法,并为运动训练学理论模型的实证检验提供了可能。其不足之处在于较难明确辨识所提取成分的物理含义。

关键词:运动训练学;运动训练数理统计;偏最小二乘回归;回归建模

中图分类号:G80-32 文献标识码:A文章编号:1006-7116(2009)10-0074-06

Application of deviated least squares regression in sports training

MA Yong-zhan

(Department of Physical Education,Taizhou University,Linhai 317000,China)

Abstract: When such variable deletion methods as OLS stepwise regression are used to process collinear data in the sports training area, they will reject some important explanatory variables or sample points out of the models, thus weakening the theoretical priority position and guidance function. The PCR model is not well capable of integrating and screening system information, and its fitting and predicting precisions are not so ideal. The PLS is well capable of integrating and screening system information, and its fitting and predicting precisions are relatively high; it is currently a very effective statistical method for processing collinear data with a small sample and multiple indexes in the sports training area, and it provides a possibility for the empirical test of theoretical models of sports training science, but it has some difficulty to specifically identify the physical meaning of components abstracted.

Key words: sports training science;sports trainingof mathematical statistics;partial least-square regression;regression modeling

运动训练领域高维数据处理的目标主要在于揭示和定量分析影响专项成绩的诸因素、评价和控制这些因素的发展水平、预测运动员专项成绩的发展趋势等3个方面。一个常用的统计处理方法就是多元线性回归。但只有当解释变量:1)数目较少;2)无多重共线性;3)各解释变量与反应变量之间的关系易于解释时,多元回归的普通最小二乘(Ordinary Least Square,OLS)估计才具有优良的理论特性[1]。然而,在运动训练领域的研究中,由于影响运动员专项成绩的诸因素之间及诸因素与专项成绩之间关系的复杂性以及优秀运动员样本量的限制,研究人员获得的往往是样本量较小、自变量指标众多且共线性(Collinearity)非常普遍的高维数据。在此条件下采用OLS回归建模,将会危害参数估计,扩大模型误差,使模型出现许多“病态”,给模型的解释带来困难[2]。近年来体育统计学科研究的重点一直致力于有关统计思想和具体方法的有效应用方面[3]。如有作者从自变量共线性的诊断和补救方法[4-5]、自变量系统的选择以及所需样本量[6-7]等方面进行了探讨,对多元回归分析应用水平的提高起到一定的促进作用。但这些研究并未从理论和方法上给出一套相对完备的方案,以解决小样本多指标共线性数据的建模问题,这无疑对运动训练理论本身的发展十分不利。近年来随着专业统计分析软件的普及,此问题已开始引起研究者的关注。本文结合实例着重从应用的角度,讨论处理这类数据的主要方法以及偏最小二乘回归法的应用效果。

1小样本多指标共线性数据的常用处理方法存在的主要问题

1.1运动训练领域共线性数据产生的原因

所谓共线性是指自变量之间存在着线性相关的现象。从统计学角度看,其成因主要有:一是自变量信息的相互重叠;二是样本量较小。从运动训练学角度看,运动训练学的很多概念之间本身就存在较高的关联性,从而直接导致对这些概念的测度指标之间的信息重叠,例如对力量与速度的测度;另一方面不同项目的优秀运动员群体本身就是小样本。基于这两方面的原因,运动训练领域数据的共线性问题几乎无法避免。当共线性问题存在时,自变量之间的信息重叠会导致一系列的数学后果,最终会使回归系数的意义变得无法解释或不可靠。因此,如何消除或减轻它对模型的不良影响,是许多学者多年来一直在探讨的问题。

1.2处理运动训练领域共线性数据的常用方法

有经验的研究者对共线性产生的不良影响非常熟悉,当他们察觉到自变量系统可能存在较严重的共线性时,便会根据分析目标采用相应的方法进行处理。这些方法大体可分成两类:一类是变量删除法,另一类为变量组合法。

1)变量删除法。

变量删除法在实际操作中有2种具体的做法:一是采用多元回归分析中的向前选择法(forward selection)、向后删除法(backward elimination)和逐步法(stepwise)对自变量进行筛选;二是先对自变量系统进行聚类,根据取大的原则筛选典型指标,然后进行回归分析[8]。有些研究者认为,既然共线性产生的主要原因是变量之间的信息重叠,筛选并删除部分相关性较高的变量,有可能会减轻或消除共线性的影响。然而,这仅仅是从统计理论和技术的角度看待这一问题,若专项训练理论和实践都要求该模型中必须包括一些重要的解释变量,而这些变量又存在着共线性,此时,研究者如何取舍将变得非常困难。例如无论采用逐步回归还是先聚类来筛选,表1(见第76页)中的自变量指标,在获得最终可解释的模型之前,研究者事先并不知道要筛选多少个指标。这样所获得的模型是由数据驱动的,理论所扮演的角色是事后的,而不是事前的。人们有理由质疑完全依赖统计技术筛选出的变量在理论上能否站得住脚,即使研究者事后给出模型修正的充分理由,也不能掩盖另一个质疑:为何这种有如此充分理由的修正没发生在研究设计阶段。从科学研究的逻辑角度讲,变量删除法已使原来的模型丧失了理论假设的地位,修正后的模型仍需新的样本来检验。也就是说,变量删除法不具备假设检验的功能,仅适用于探测性的研究[9]。研究者应该清醒地认识到变量删除法意味着对原有理论模型的修改,而完全基于数据资料的模型修改,会将本应保留的系统信息舍弃,给模型的解释带来困难,增加了错误决策的风险。换言之,这种“后见之明”的作法,会严重削弱理论的优先地位和导向功能,进而威胁到理论本身的发展。

2)变量组合法。

变量组合法的实质是将多个相关性很高的自变量视为潜变量(也称因子或成分)的显性测度,然后寻找潜变量与各显性测度指标之间的线性组合关系,再用潜变量进行回归分析。变量组合法可保留系统中的所有自变量,而无需改动事先建构好的理论模型,这样从研究的逻辑角度看,为假设检验提供了可能。主成分回归(principle component regression,PCR)和偏最小二乘(partial least square,PLS)回归可以说是最典型的变量组合法,不过两者提取成分的工作原理并不相同。在主成分回归时,首先抽取自变量集合中的主成分,这些主成分均可表达为自变量的线性组合。由于主成分之间不存在相关现象[10],用主成分对因变量进行回归建模,这就有可能避免直接使用最小二乘法在参数估计时的困难。但这种方法在主成分提取的过程中,并没有考虑与因变量的关系,提取的几个主成分虽然对自变量系统有很强的解释力,但对因变量的解释能力很差,况且提取多少个主成分也颇受争议。因此,利用主成分回归的效果未必理想。例如,对表1中的数据提取2个主成分,其方差累积贡献率为79%左右。但当把这2个主成分与原来的11个自变量平等放在一起,无论采用何种方法筛选变量,这2个主成分都无法进入方程。该结果直观地说明,这2个主成分并不比原有的11个自变量对因变量的解释能力强。所以,在实际应用中对利用主成分回归消除高维数据中自变量之间的共线性问题要非常慎重,不要轻易舍弃对自变量系统解释力较小的成分,也许那些对自变量系统解释力较小的主成分,反而对因变量具有更强的解释作用。

为了弥补主成分回归在提取成分上的缺陷,偏最小二乘回归法分别在自变量集合X和因变量集合Y中提取成分t1和u1。但提取这两个成分时,要同时满足两个条件:1)t1和u1应尽可能大携带他们各自数据表中的变异信息;2) t1和u1的相关程度能够达到最大。这两个条件表明,t1和u1应尽可能好的代表数据表X和Y,同时自变量的成分t1对因变量的成分u1又有最强的解释能力。在第一个成分t1和u1被提取后,偏最小二乘回归分别实施X对t1的回归以及Y对t1的回归,如果回归方程已经达到满意的精度,则算法终止;否则,将利用被解释后的残余信息进行第二轮的成分提取,直到能达到满意的精度为止。具体算法详见参考文献[11-12]。

从以上偏最小二乘回归的工作原理看,它所提取的主成分不仅对自变量系统具有最强的解释作用,同时也对因变量系统的解释能力达到最大。经过这样的信息综合与筛选后,对因变量没有解释意义的信息就被排除了。与主成分回归相比,偏最小二乘回归方法更具先进性,计算结果也更可靠。它所有的计算过程均可由专门软件SIMCA-P、SPSS 16 或SAS 8.0以上版本实现。因此,近几年引起了广泛的重视。

2实例分析

2.1资料来源和特征

采用曲淑华等[13]对我国20名优秀铁饼运动员专项力量指标与专项成绩的测试数据,其中以y表示专项成绩(m),x1~x11分别代表原地掷饼(m)、掷重饼(m)、掷轻饼(m)、后抛铅球(m)、立定跳远(m)、定立三级跳远(m)、抓举(kg)、卧推(kg)、高翻(kg)、深蹲(kg)、半蹲(kg)11项专项力量素质指标(见表1)。

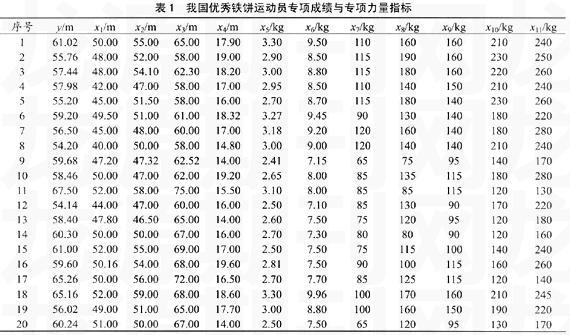
该资料有11个自变量,而样本量只有20个,若使用SPSS统计分析软件进行共线性诊断,将会发现有6个自变量的方差膨胀因子(VIF)均大于15,表示这些变量之间可能存在较严重的共线性问题。进而可根据条件指数(condition index)和方差比例(variance proportions)确定自变量x2、x3和x10之间具有很强的线性组合关系。若此时采用强行法(enter)进行普通最小二乘回归,决定系数高达0.876,方程的F检验值远大于检验临界值,也就是说,y与x1,…,x11之间应该存在很好的线性关系。但所有回归系数的t检验在0.05水平上皆通不过,说明该数据的多重共线性问题已严重危害到参数估计。这种小样本多指标共线性的数据正是运动训练领域的研究中使研究人员感到非常困扰的问题。

2.2自变量共线性条件下变量删除法与变量组合法建模比较

由于表1数据中自变量之间的共线性已危害到最小二乘参数估计,若研究者使用普通最小二乘逐步回归法筛选变量,试图消除或减轻共线性的不良影响,最终只能选取了一个自变量x3(掷轻饼),而其他重要的变量都被排除于模型之外。若先对自变量系统聚类筛选典型指标,然后进行回归也会得到相类似的结果。这些结果无论从专项训练理论和实践的角度都很难让人们接受。所以,用变量删除法消除共线性并非总是可取的,即使在探测性的研究中,也不一定能取得满意的效果。

为了进一步比较PLS与PCR回归在处理自变量共线性问题方面的优劣,将表1中的数据分成两个部分:前15个作为拟合数据,后5个作为预测数据。在进行主成分回归时,根据特征值大于1的原则选取了3个主成分,然后用因变量Y与这3个主成分回归,第3个主成分无法通过t检验。故只能选取前了2个主成分。根据交叉有性Q2≥0.097 5(临界值)的决策准则[10-11],偏最小二乘回归也选取了2个主成分。它们对各自变量系统概括的信息大体相同,方差累积贡献率均为79%左右。以上3种方法的回归系数估计值列于表2。

从表2可见,PCR和PLS回归方程中自变量抓举(x7)、卧推(x8)、深蹲(x10)、半蹲(x11)的回归系数均为负值,这与它们和专项成绩(Y)的简单相关系数的方向是一致的。该现象也可从专项训练理论和实践的角度得到很好的解释。抓举(x7)、卧推(x8)、深蹲(x10)、半蹲(x11)反映运动员的最大力量水平。虽然最大力量水平是铁饼运动员的主要特征之一,也是提高专项投掷能力的基础,但这并不意味着最大力量与专项成绩之间具有良好的线性关系,尤其对高水平的运动员更是如此[12-13]。因此,这两个模型中,抓举(x7)、卧推(x8)、深蹲(x10)、半蹲(x11)的回归系数取了非常小的负值。值得注意的是,PCR模型中另一个重要的自变量x9(高翻)没有包括进去。总体而言,与变量删除法相比,PCR和PLS回归模型更符合人们的认识水平。

2.3PCR与PLS回归模型的精度比较

PCR和PLS模型的精度可从所提取的综合变量(或成分)对自变量系统信息的利用率及对因变量系统的解释率;方程的拟合和预测精度两个方面分析。

在PCR和PLS回归建模中,如果提取的综合变量对自变量系统信息的利用率越高且对因变量系统的解释率越大,说明它携带更多的自变量系统X中的变异信息参与了建模,同时尽可能多地解释了因变量Y中的变异信息。这样,用于分析过程的信息越多,并对因变量的解释作用越大,方程的精度就越高,预测效果也就越好。PCR和PLS方程精度计算结果见表3。

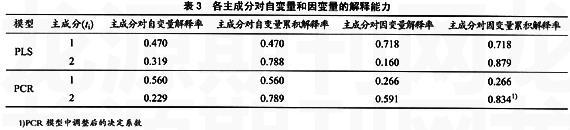
从表3可看出,PCR和PLS提取的2个主成分对自变量的信息利用率均为79%左右,但它们对因变量的解释量却不同,PLS对因变量的解释量明显高于PCR,这表明PLS模型的精度要明显高于PCR。在PLS回归模型中第1主成分t1解释了原自变量系统47.0%的变异信息,同时解释了因变量系统71.8%的变异信息,第2主成分t2解释了原自变量系统31.9%的变异信息,同时解释了因变量系统16.0%的变异信息。在PLS模型中第一主成分t1既是对自变量系统信息概括能力最大的成分,也是对因变量系统最具解释作用的成分。而PCR模型中最能概括自变量系统信息的第1主成分t1对因变量的解释作用仅为26.6%,远不及第2主成分t2对因变量的解释作用。这与PCR提取主成分的方式有关。PCR在提取主成分的过程中,只是针对自变量系统寻找有代表性的主成分,所提取的主成分虽可反映自变量系统的重要信息,但与因变量的关系极小。而那些与因变量相关性较大,但在自变量中所占比例小的成分却有可能被删除。因此,在应用PCR处理高维数据自变量之间的共线性问题时,切不可盲目认为对自变量系统解释作用大的成分,一定会对因变量的解释作用也大,故不可轻易舍弃对自变量系统解释力较小的成分,否则会影响模型的精度。从本实例中亦可看出,PLS较PCR对系统信息的综合与筛选能力更强。

PLS和PCR模型的拟合和预测精度,可通过4项综合指标进行比较。这4项指标分别是:Coef为真值和预测值的相关系数、SSE为残差平方和、AveErr为绝对误差的平均值、AveErrPer为相对误差的平均值。从表4可见,在变量间存在高度共线性,自变量个数比较多而观察例数较少的情况下,主成分回归无论是拟合效果还是预测效果,均不如偏最小二乘回归理想。

2.4自变量xj在解释因变量y时的作用

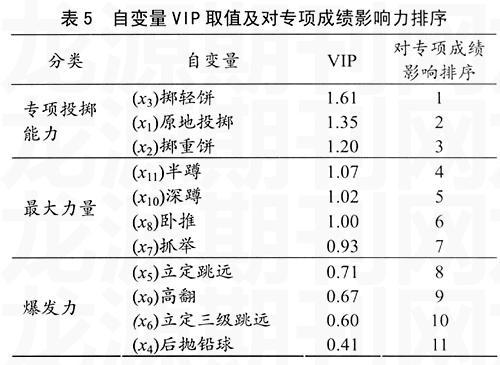
考察每一个自变量xj在解释因变量y时的作用,是运动训练领域数据处理的主要任务之一,也是教练员最为关心的问题。其目的在于以量化的形式说明各因素对专项成绩的影响大小,提高运动训练的科学化水平。由于自变量之间存在着共线性问题,模型中的某一自变量对因变量的解释效应要分摊于其它几个变量,回归系数已不再是各自变量的边际效应。因此,OLS和PCR模型中的回归系数大小无法准确测度自变量对因变量的影响程度。PLS回归模型在测度自变量对因变量影响的重要性程度时,并非直接比较各自变量的标准化回归系数,而是使用变量投影重要性指标VIP(variable importance in projection)。在PLS回归中自变量对因变量的解释是通过各成分传递的。如果某成分对因变量的解释作用很强,而自变量在构造该成分时的权重系数很大,则该自变量对因变量的解释能力就越大。VIP就是根据自变量xi在构造成分时的边际贡献大小,来反映自变量对因变量的解释作用。其取值见表5。

从VIP取值可以看出,对优秀铁饼运动员专项成绩具有最大影响力的前3项指标,其动作特征均与掷铁饼技术本身紧密关联,集中反映了以整体性和综合性为特征的专项投掷能力。半蹲、深蹲、卧推和抓举4项指标的VIP值较接近,反映运动员的最大力量水平。立定跳远、高翻、立定三级跳远和后抛铅球主要反映运动员爆发力,它们的VIP值相对小些。该结果亦提示优秀铁饼运动员专项素质是由专项投掷能力、最大力量和爆发力3个递进的层次构成。这一结果与专项训练理论和实践十分吻合[13-14],不过,在PLS回归分析中,研究者很难通过自变量在构造成分t1和t2时的权重系数,明晰地辨识出这两个成分的确切含义,也就无法清楚地知道究竟什么因素在整个建模过程中起着主导性的作用。这也是PLS方法在应用中有待解决的问题。故有关小样本多指标共线性数据处理方法的应用

3结论

1)OLS逐步回归变量删除法在处理运动训练领域的共线性数据时,会将一些重要的解释变量或样本点排除在模型之外,削弱了理论的优先地位和导向作用,不利于理论本身的发展。PCR模型对系统信息的综合与筛选能力不佳,拟合与预测精度不甚理想。

2)与其他几种方法相比,PLS回归方法具有完善的理论体系,对系统信息的综合与筛选能力强、拟合与预测精度较高,是目前处理运动训练领域小样本多指标共线性数据的一个非常稳健的统计方法,可同时实现高维数据处理的主要目标,并为运动训练学理论模型的实证检验提供了可能。其不足之处在于较难明确辨识所提取成分的物理含义。

参考文献:

[1] Rao C R,Toutenburg H. Linear Models[M]. New York:Springer-Verlag Press,1995:67-71.

[2] 何晓群. 回归分析与经济数据建模[M]. 北京:中国人民大学出版社,1997:5.

[3] 陈及治,蔡睿,程致屏,等. 体育统计学科进展[C]//体育科学研究现状与展望. 北京:中国体育科学学会,2000.

[4] 魏登云. 多元共线性分析及其在体育科研中的应用[J]. 安徽师大学报:自然科学版,1996,24(1):75-79.

[5] 马勇占. 试论多重共线性对体育科研中线性回归模型的危害及其诊断和补救方法[J]. 体育科学,2002,22(6):112-115.

[6] 刘炜. 线性模型在体育科研中应用的常见误区分析[J]. 上海体育学院学报,2001,25(4):23-26.

[7] 刘厚生. 回归分析方法在体育科研中的应用初探[J]. 体育科学,1993,17(3):75-78.

[8] 孙有平. 优秀男子铁饼运动员竞技能力某些决定因素综合评价的研究[J]. 成都体育学院学报,2002,28(6):64-67.

[9] 张力为. 体育科学研究方法[M]. 北京:高等教育出版社,2002:348-357.

[10] Stone M,Brooks R J. Continuum regression: Cross-validated sequentially constructed prediction embracing ordinary least squares,partial least squares and principal components regression[J]. Journal of the Royal Statistical Society (series c),1990:237-269.

[11] 王惠文. 偏最小二乘回归方法及其应用[M]. 北京:国防工业出版社,2000:178-200.

[12] 蒋红卫,夏结来. 偏最小二乘回归及其应用[J].第四军医大学学报,2003(4):280-283.

[13] 曲淑华,孙有平,张英波. 对我国优秀铁饼运动员专项力量训练现状的研究[J]. 北京体育大学学报,2001,24(1):108-123.

[14] 袁作生,南仲喜. 现代田径运动科学训练法[M].北京:人民体育出版社,1997:440-448.

[15] 张景龙. 铁饼运动员的力量训练[J]. 田径,2003(9):16-17.

[编辑:周威]