《勾股定理》教学设计比较研究

李庆辉

● 教学片段对比展示

片段一:多媒体环境

深圳市深南中学王菁

创设情境:教师介绍勾股定理的历史和逸闻趣事,设置勾股定理相关问题串。学生欣赏探索勾股定理(见图1)和消防员架梯子救火动画(见图2)。从有趣的情境出发,以境激情,以情激思。

师生互动,探索新知:学生以小组合作、交流的形式,采用直接数方格的办法,或者是分割成几个等腰三角形完成实验,计算正方形A、B、C的面积(见图3)。利用几何画板课件演示,形象地展现了定理的一般性,更好地帮助学生理解定理。

回归生活,应用新知:一根旗杆在离地9米处断裂,旗杆顶部落在距底部12米处,旗杆折断之前有多高?学生体会此题的实际背景,并探讨“旗杆折断之前的高度”指的是什么。使学生全面了解和灵活掌握直角三角形三边关系,防止思维定势。

片段二:网络技术环境

河北省唐山市第十七中学王立民

创设情境:以贴近学生生活的实际问题引入(一个门框的高为2米,宽为1米。一块长3米,宽2.2米的薄木板能否从门框通过,为什么),从而调起学生渴求知识的胃口,激发和点燃学生的学习兴趣,增大主体参与程度。

大胆猜想:我们以“勾3、股4、弦5”的情况为例进行猜想。看看动画(见图4)能不能带给你一些灵感,请你大胆地猜想一下吧!

动画比较直观,学生容易猜想,并且这个动画也展示了用面积来证明勾股定理的一个方法,为解决这节课的难点——勾股拼图做了铺垫。

计算机验证:找更多的直角三角形进行测量、计算,再实验。如果在练习本上画、测、算,必定费时费力;利用几何画板,可以减少大量的测量和计算,并且测量和计算也相对准确一些。该过程中几何画板软件的应用,为探索数学提供了数值的方法,它可以拖动三角形的一个顶点,任意改变直角三角形的大小,在变化中可以看到,不变的是a2+b2的数值据永远等于c2。

理性认识:利用几何画板,动手拼接图形,探究证明思路。

以上是参赛的两个教学片段,纵观2006～2008年三届优质课大赛,初中数学组的参赛教师有10%选择了《勾股定理》作为参赛课,他们根据自己的实际、自己的理解,应用不同的教学环境、采用不同的教学方法和策略教学同样的主题。但其中有些教师采用的多媒体环境和网络环境下的教学模式,忽视了传统教学方法的应用,未能达到理想的教学效果。其主要原因是对信息技术与课程整合的整合点理论理解不透彻。

● 整合点深度分析

(一)优质课大赛《勾股定理》教学设计分析

《勾股定理》是初中数学教学的重要内容之一。一方面,勾股定理可以看作直角三角形的性质,它揭示了直角三角形的三边的数量关系,把形的特征(直角三角形的一个角是直角)转化为数量关系(三边符合a2+b2=c2),解决了许多直角三角形的计算问题;另一方面,由于勾股定理在整个数学学科以及重大科技发现中的作用,对学生的发展,尤其是科技观的形成,其影响是重大的。笔者认真研究了2006～2008年三届优质课大赛的教学设计,发现信息技术主要是用做创设情境工具、演示工具和探索工具。经统计,在全部的18节课中,信息技术被用来创设情境的有17节课,占94%;用做演示工具的有18节课,占100%;用做探索工具的有17节课,占94%;用做交流工具的仅有3节课,占17%;学生利用网络收集信息的有5节课,占28%;学生在网络环境下动手操作的有9节课,占50%;学生在非网络环境下动手操作的有7节课,占39%。

从统计的结果不难看出,多数教师忽略了传统教学方法的优势,信息技术似乎成了万能工具,而多媒体环境下的教学却不能找到恰当的整合点。笔者从整体上分析了勾股定理的教学设计存在的共性优缺点。

优点:①利用多媒体手段从中、西方不同的文化背景入手,挖掘勾股定理的发现过程,中西对比,培养学生的爱国情操。②充分利用多媒体技术创设教学情境,把教学内容与日常生活有机地联系起来,突出了勾股定理的应用。③能充分利用多媒体等教学资源,较好地使用教具,让学生在演示中形象地理解题意。④利用几何画板软件,直观体验了任意性的含义,能使学生深入理解任意性在数学中所起的作用。

缺点:①弦图证法和毕达哥拉斯证法是一亮点,应该让学生通过合作拼图,进行勾股定理的证明,这也是这堂课的难点。而很多教师将这一系列的数学活动利用多媒体完成,学生未能更好地主动尝试、探索,主动了解和发现知识的产生与发展过程。②在网络教学中教师没能设置任务,引导学生利用丰富的网络资源自主探究有关勾股定理的发现、发展、文化价值等资料。搜集资料这一过程多由教师一人包办。③对整合点和整合点诊断过程缺乏了解,找不到恰当的整合点。对信息技术与课程整合还存在盲目性,有些教师还是为了用信息技术而用。

(二)《勾股定理》教学设计普遍存在的问题及原因

1.对《勾股定理》教材安排特点把握不准。

《勾股定理》教材安排有如下特点:①勾股定理有着悠久的历史,是人类最伟大的数学发现之一。但是由于教材在编写过程中遵循了简约性的原则,没能更深入地介绍它产生、发展的历史背景以及它在人类文化发展史上的贡献。②缺少多样的验证方法。勾股定理的证明方法很多,不同版本的教科书上都是选择了一到两种的面积证法。而学生学习这些证明法又存在以下两方面的困难:一是这种方法以前没见过,感到陌生,尤其是觉得不像证明。这主要是因为教科书中没有专门讲面积的理论,推理的根据不明确造成的。教学时可以向学生说明,图形经过割补拼接后,只要没有重叠,没有空隙,面积不会改变,这是一种常用的证明方法,这也是我国古代证明几何问题常用的方法。二是教材中的证明方法是利用面积关系列等式,而如何找到这个等式对学生来说又是一个难点。

2.对整合点理论理解不透彻。

参赛选手的信息技术素养较高,但对整合点理论的理解不深入、不透彻是普遍存在的问题。导致某些教师的教学效率没有显著提高,没有激发学生的学习兴趣,自主与协作学习、动手操作能力没有得到更好的培养。

整合点的诊断过程是,首先要分析每一个理想教学步骤是否能够在常规教学手段支撑下完成,完成的效率和质量如何;然后分析信息技术手段对每一步的支撑情况如何,是否比常规教学手段质量或效率高,如果确实高的话,该步骤就可以诊断为整合点。

一节课的整合点应从这节课的教学重点、难点所对应的教学步骤中诊断,其他目标所对应的教学步骤中即便有整合点,利用信息技术解决了整合点的问题,对一节课的教学质量和效率提高所起的作用也是很有限的。一节课的教与学的质量和效率主要取决于重点、难点的解决程度。对于其他的教学目标所对应的教学步骤,是否分析整合点,要根据这节课的具体情况而定。同一节课,不同学校、不同班级、不同教师所设计的教学过程可能有区别,因此,整合点可能有区别。即便教学过程相同,整合点也可能不同。整合点是教学步骤,而不是教学内容,在整合点诊断时不要搞混淆了。

综合教材安排特点、学生认知特征、教学环境、教学资源等各方面的因素。结合整合点理论,笔者认为对于《勾股定理》这节课采用混合式教学会达到理想的教学效果。

● 点石成金——理想状态下的勾股定理教学设计

所谓理想情况下一节课的教学过程设计,是指在不考虑教学条件的情况下,突破时空限制来构思课堂教学的步骤,尽可能提高学生的学习质量和效率。笔者根据整合点理论,及优质课大赛中各位教师的优点。笔者设计了理想状态下的勾股定理教学设计,下面是理想状态下教学设计的几个片段。

(一)穿越表象,透视规律

教与学的活动以及媒体的应用:

1.观察下图并填空。

(1)请学生观察图形A、B、C的面积有什么关系(见图5)?(SA+SB=SC)

(2)图6中每个小方格代表一个单位面积,正方形A中含有____个小方格,即A的面积是____个单位面积;正方形B的面积是____个单位面积;正方形C的面积是____个单位面积。

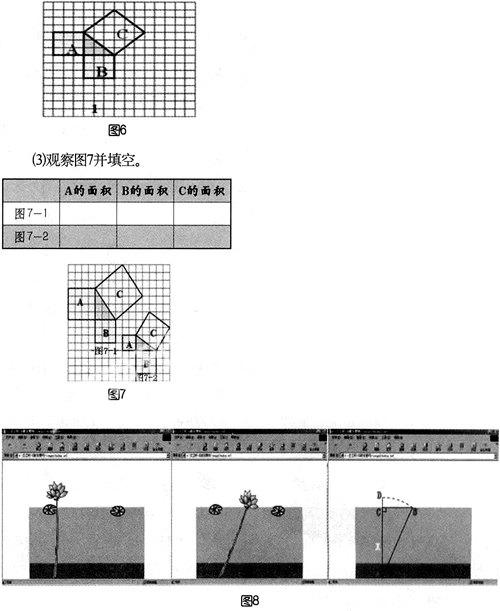
三个正方形A、B、C面积之间有什么关系?(SA+SB=SC,即两条直角边上的正方形面积之和等于斜边上的正方形的面积)

(4)做一做。

学生利用几何画板画出任意一个直角三角形,并推导出直角三角形三边平方和的关系。

整合点及解决办法:①设置“数格子”、“超级画板演示”、“几何画板实验”三个环节,让学生直观感受勾股定理的数形特征,亲历猜想勾股定理的过程。②充分运用信息技术的优势,直观、形象地揭示问题的本质,让学生在变化中把握住“不变”的本质,进一步强化猜想的正确性,从而激发学生进一步论证猜想的欲望,维持强劲探索动力,为下一步学习活动做好充分的思维准备。

(二)例题讲解,运用定理

教与学的活动以及媒体的应用:

1.在Rt△ABC中,∠C=90°。

(1)已知a=6,c=10,求b。

(2)已知a=40,b=9,求c。

(3)已知c=25,b=15,求a。

2.在Rt△ABC中,∠C=90°

(1)若2∠A=∠B,且a=2,则b=_____,c=____。

(2)a:b=3:4,且c=10,则a=____,b=____。

利用实物投影展示学生的求解过程。

整合点及解决办法:①习题设计遵循“循序渐进”,强化学生对定理的理解、运用,培养学生解决实际问题的能力。②通过实物投影展示学生的学习成果,让学生互相进行点评。

(三)巩固练习,强化记忆

动画演示莲花问题:平平湖水清可见,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何见深浅(见图8)。

整合点及解决办法:利用多媒体生动、形象地再现问题情境。

(四)思维拓展,深化定理

教与学的活动以及媒体的应用:已知任意△ABC,其三边分别为a、b、c,让学生动手操作,仔细观察几何画板动画演示,并分小组讨论,完成下面的内容。

①当△ABC是三角形时,a²+b²>c²。

②当△ABC是三角形时,a²+b²=c²。

③当△ABC是三角形时,a²+b²2