哈夫曼树在分类问题中的应用

宋　颖　赵大伟　刘思远　毕明超

[摘要]分类是一种常用运算，其作用是将输入数据按预定的标准划分成不同的种类。虽然解决分类问题的方法很多，但利用哈夫曼树可谓是求解给定问题的最佳分类方法。因此，首先阐述哈夫曼树的原理，然后以根据检测结果划分产品质量等级为例进一步论述哈夫曼树的主要技术及实现，最后总结哈夫曼树的优势。

[关键词]哈夫曼树 分类 判定树 哈夫曼算法

中图分类号：O24文献标识码：A文章编号：1671－7597（2009）0510054－02

一、引言

树有广泛的应用，其中一类重要的应用是描述分类过程。分类是一种常用运算，其作用是将输入数据按预定的标准划分成不同的种类。例如，将学生考试的百分制成绩转换为不及格、及格、中、良好、优秀，那么如何由分数段的值确定其分级就是一个分类问题，学生成绩分布情况见表（一）。

再如，某工厂对其产品质量进行自动检测，并根据检测结果划分产品质量等级，如何由产品的检测结果值m确定其质量等级也是一个分类问题，等级标准见表（二）。

用于描述分类过程的二叉树称为判定树。判定树的每个非终端结点包含一个条件，因而对应于一次比较或判断；每个终端结点包含一个种类标记，对应于一种分类结果。如图1(a)、(b)所示为上述求解产品的质量分类问题的两棵判定树，其中每颗树上的每个非终端结点都对应五个条件判断，即对检测m的五次比较。

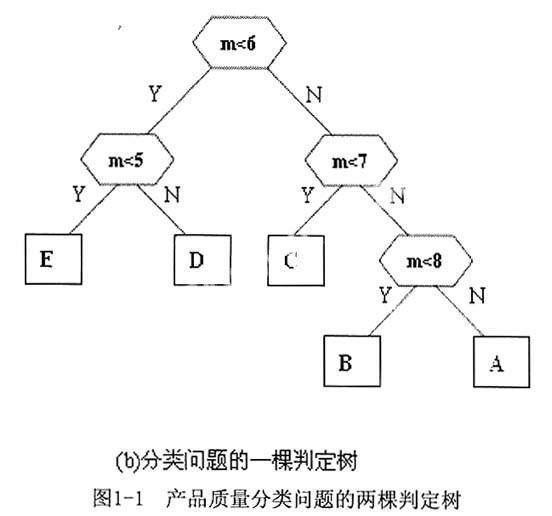
那么究竟将这个分类过程表示成哪一棵判定树，才能使其执行时间最短呢？让我们对上述判断框做一具体的分析。假设需要分级的产品有N=100000件，并且这批产品的等级分布如表（二）中表格的第三行所示。对应图1-1(a)、(b)中的比较次数分别如表（三）所示。

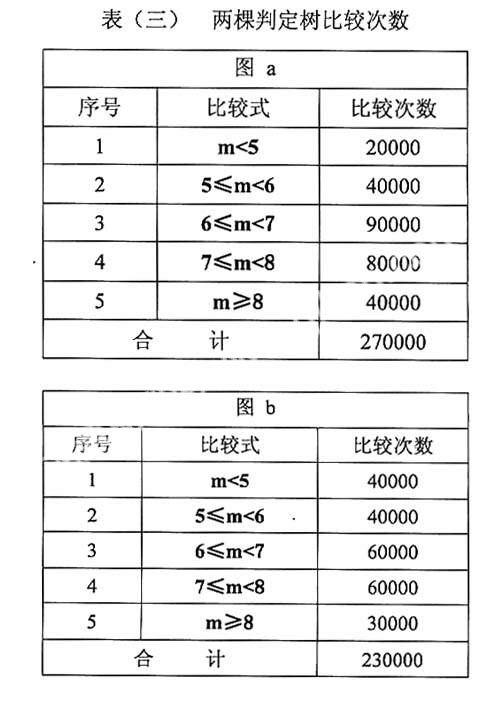
相对而言，图1(b)这棵判定树对所有产品定级，总比较次数比图1(a)将少做40000次比较，平均比较次数也下降为2.3。这说明，按不同判定树进行分类的时间复杂性是不同的，有时可能相差很大，因此，怎样能构造出时间性能最高判定树是一个值得研究的问题。

二、哈夫曼树的原理与技术

为解决上述分类问题，首先必须找出一种一般化的方法以确定任一判定树的平均比较次数。设T是一判定树，其终端结点为N1，...，NK。每个终端结点Ni对应的百分比为Wi，这里W1+W2+...+Wk=1。通常将Wi称为Ni的权。再假定Ni的祖先数为Li。为区分出Ni对应的分类结果需做Li次比较。在图(b)所示的判定树上,叶子B的祖先有三个，它们正好是为区分出等级B进行的三次比较。这样，按T进行分类的平均比较次数为WPL(T)=(∑(Wi*N*Li))/N＝∑Wi*Li(i＝1..k)上述问题可重新表述为：给定一组值W1，...，

Wk，如何构造一棵有K个叶子且分别以这些值为权的判定树，使用权得其平均比较次数最小。满足上述条件的判定树称为哈夫曼树。

一般情况下，最优二叉树中，权越大的叶子离根越近。那么，如何构造最优二叉树呢？哈夫曼（Haffman）依据这一特点于1952年提出了一种简单而有效的方法，这种方法的基本思想是：

1．由给定的n个权值{W1，W2，…，Wn}构造n棵只有一个叶结点的二叉树，从而得到一个二叉树的集合F＝{T1，T2，…，Tn}；

2．在F中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树，这棵新的二叉树根结点的权值为其左、右子树根结点权值之和；

3．在集合F中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到集合F中；

4．重复2、3两步，当F中只剩下一棵二叉树时，这棵二叉树便是所要建立的哈夫曼树。

三、哈夫曼树的实现

（一）哈夫曼树在分类中的实现

以表（二）中第三行的五个百分比为给定值，按上述哈夫曼算法建立哈夫曼树的过程如下。

1．先按给定的权值构造5棵二叉树如图3-1（a）所示；

2．再取0.1，0.2另外构造一棵新的二叉树如图3-1（b）所示；

3．再取0.2，0.2另外构造一棵新的二叉树如图3-1（c）所示；

4．再取0.3，0.3另外构造一棵新的二叉树如图3-1（d）所示；

5．再取0.4，0.6另外构造一棵新的二叉树如图3-1（e）所示，即哈夫曼树。

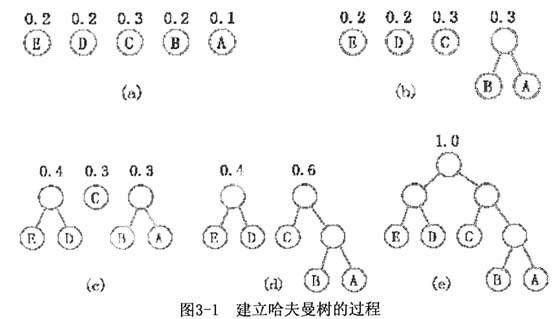
在得到的哈夫曼树图3-1(e)所示的各个非终端结点上设置适当的条件，就得到图1-1(b)所示的判定树。因此，这一判定树描述了求解给定问题的最佳分类方法。

（二）哈夫曼的算法

由上述哈夫曼树的原理可知，最终求得的哈夫曼树中共有2N-1个结点，其中N个叶结点是初始森林中的N个孤立结点，并且哈夫曼树中没有度数为1的分支结点。由于结点数已知且固定不变，可采用静态链表作存储结构。设置一个大小为2K-1的数组，令数组的每个元素由四个域组成，它们分别用于存储权值、双亲指针和左右孩子指针。在这种存储结构上的哈夫曼算法可描述如下：

1．将哈夫曼树向量(T类型为hftree)中的2n-1结点初始化：即将各结点中的三个指针和权值均置为0。

2．读入N个权值放入向量T的前N个分量中，它们是初始森林中的N个孤立的根结点上的权值。

3．对森林中的树进行N-1次合并，共产生N-1个新结点，依次放入向量T的第i个分量中(N+1<=i<=M〉。每次合并的步骤是：

（1）在当前森林的所有结点T[j](1<=j<=i-1)中，选取具有最小权值和次小权值的两个根结点，分别用x和y记住这两个根结点在向量T中的下标。

（2）将根为T[X]和T[y]的两棵树合并，使其成为新结点T[i]为根的二叉树。同时修改T[x]和T[y]的双亲域parent，使其指向新结点T[i]，这意味着它们在当前森林已不再是根。将T[x]和T[y]的权值相加后作为新结点T[i]的权值。

void huffman(int k,float W[k],hftree T)

/*求给定权值W的哈夫曼树T*/

{ int i,j,x,y;

float m,n;

for (i=0;i<2*k-1;i++) /*置初值*/

{ T[i].parent=-1; T[i].lchild=-1; T[i].rchild=-1;

if (i

else T[i].wt=0

}

for (i=0;i

{ x:=0; y:=0:m=maxint: n:=maxint;

for (j=0;j

if ((T[j].wt

{ n=m; y=x; m=T[j].wt; x=j; }

else if ((T[j].wt

{n=T[j].wt; y=j };

T[x].parent=k+i; T[y].parent=k+i; /*合并成一棵新的二叉树 */

T[k+i].wt=m+n;

T[k+i].lchild=x; T[k+i].rchild=y;

}

}

四、结束语

哈夫曼树和哈夫曼算法的应用十分广泛，根据不同的应用需求可以对哈夫曼树做不同的解释，即赋予不同的含义。本文详加讨论的问题只是其中的一种解释。虽然解决分类问题的方法很多，但利用哈夫曼树可谓是求解给定问题的最佳分类方法。

参考文献：

[1]严尉敏、吴伟民，《数据结构（C语言版）》[M].北京：清华大学出版社，2001.

[2]陈元春、张亮、王勇，《实用数据结构基础》[M].北京：中国铁道出版社，2008.

[3]徐孝凯，《数据结构实用教程》[M].北京：清华大学出版社，2000.

[4]包振宇、孙干，《数据结构》[M].北京：中国铁道出版社，2006.

作者简介：

宋颖，副教授，技师，白城职业技术学院信息工程系主任。