改进的三维点集凸包求取算法
张 飞 谢步瀛 闫星宇 刘 政
摘 要:为提高三维点集凸包的求取效率,提出充分利用凸包极值点和性质改进的三维点集凸包求取算法.首先,求出三维点集中的极值点,并由它们形成初步凸包;其次,根据初步凸包与点的位置关系,排除其内部点;最后,依次考察其外部点,求出符合要求的点集、棱边集和面集,并对凸包进行扩展,得到凸包的点集、棱边集和面集.与普通算法进行时间的复杂度分析比较及实验表明,该算法效率较高.
关键词:三维点集;凸包;极值点
中图分类号:TP212.12;O241.82
文献标志码:A
Improved algorithm on determining convex hull of 3D point set
ZHANG Fei,XIE Buying,YAN Xingyu,LIU Zheng
(College of Civil Eng.,Tongji Univ.,Shanghai 200092,China)
Abstract:To improve the computation efficiency of convex hull of 3D point set,an improved algorithm on determining convex hull of 3D point set is proposed by making full use of the extreme points and the character of the convex hull. Firstly,the extreme points in 3D point set are obtained to make up of the initial convex hull. Secondly,the internal points of the convex hull are eliminated according to the position relationship between the initial convex hull and the points. Finally,the external points are examined in turn,the point set,line set and face set that meet the requirements are acquired,and the convex hull is expanded to obtain the final point set,line set and face set of the convex hull. The comparison of time complexity analysis with normal algorithms and the experiments indicate that the algorithm has higher efficiency.
Key words:3D point set;convex hull;extreme point
0 引 言
点集凸包问题是计算几何学中基本、常见的问题,通常可以分为二维凸包和三维凸包.[1]二维凸包被广泛应用于模式识别、图像处理和设计自动化等领域[2];三维凸包被广泛应用于计算机仿真、建筑体建模、卫星通信和无线电广播等领域[3].二维凸包算法相对比较简单、成熟,已有很多研究成果.随着计算机软件和硬件技术的发展,处理三维的问题越来越多,有必要进一步研究三维凸包算法.本文在现有二维和三维凸包算法的基础上,提出1种改进的三维点集凸包求取算法.
自20世纪70年代以来,不少学者提出有关点集凸包的算法,较为经典的有卷包裹法、格雷厄姆法、分治法、增量法以及周培德在文献[1]中提出的Z3—1和Z3—2算法.在这些算法中,卷包裹法、分治法、增量法以及Z3—2算法能够推广到三维.同样,也有很多二维算法不能推广到三维,比如格雷厄姆法和文献[4]提出的算法.
在绝大多数情况下,二维凸包和三维凸包由点集中的部分点构成,其余点则在凸包内部.所以,点集中的点可分为凸包顶点和内部点,因而可以考虑利用一些特殊点(如极值点)先构成凸包大体形状,再排除内部点中的部分点,以减少点的数目来提高算法效率,这就是快速凸包技术[5].这种思想显然也适用于三维点集凸包算法.
在快速凸包技术的基础上,本文给出1种改进的凸包求取算法.与传统快速凸包算法相比,本文算法考虑采用更多的极值点,更充分地利用极值点性质,缩小点的搜索范围,提高算法效率.
1 定义及性质
定义1 凸包.即凸包多面体,把多面体的任何1个面无限延展,其他面都在这个延伸面的同一侧.[1,6]文中的点集凸包是指包含点集中所有点的最小凸多面体.凸包的面均由三角形组成,即使真实的面由多边形组成,这些多边形也均被分割成三角形.
定义2 一维极值点.在三维点集中,若只考虑点的3个坐标中的1个坐标并求取其最大值或最小值,所求得的这些点称为一维极值点.如果最大极值点和最小极值点都不止1个,则所有最大极值点在同一平面,所有最小极值点也在同一平面内.
定义3 二维极值点.在三维点集中,如果把所有点都投影到1个坐标平面上(如xOy平面,yOz平面,zOx平面),然后在平面上求取极值点,称这些点为二维极值点.现以投影到xOy平面为例定义二维极值点.在平面点集中,分别称具有最小和最大x坐标值的点构成的子集为Xmin子集和Xmax子集;分别称具有最小和最大y坐标值的点构成的子集为Ymin子集和Ymax子集.在Xmin子集中,称对应y坐标的最小的点为左下点,称对应y坐标最大的点为左上点;在Xmax子集中,称对应y坐标的最小的点为右下点,称对应x坐标最大的点为右上点;在Ymin子集中,称对应x坐标最小的点为下左点,称对应x坐标最大的点为下右点;在Ymax子集中,称对应x坐标的最小的点为上左点,称对应x坐标最大的点为上右点.
定义4 极值点.包括一维极值点和二维极值点.在现实情况下,某点可能既是一维极值点也是二维极值点.在算法应用的过程中并不严格区分.
性质1 空间中给定的若干个点的凸包是唯一的,且凸包的顶点必须是原给定点集中的点.[3]
性质2 极值点必为凸包的顶点中的点.
性质3 在三维点集中,必存在一维极值点,且至少有1个.如果只有1个一维极值点,则凸包为平面,这种情况将不形成凸包.所以,构成凸包的点集中,至少有2个一维极值点.
性质4 在三维点集中,必存在二维极值点,且至少有2个.当且仅当为2个极值点时,在投影平面内查找离由这2个点构成的直线最远的点作为极值点.如果不存在,则点集不构成凸包.这样,至少有3个极值点,最多8个极值点存在.即三维点集中,二维极值点可以构成1个平面或者空间凸环.文献[4]中给出的在二维情况下的证明,也适用于三维点集中二维极值点的情况.
推论 由性质3和性质4,在三维点集中,只要存在凸包,即所有点都不在同一平面上,由极值点可以构成1个初步凸包.
2 算法思路描述
求取三维点集的凸包,一般要求求出凸包的顶点集、棱边集以及面集.当然,在3个集合中,顶点集和面集是必需的,棱边集可以由面集直接推出.
算法的总体思路是:通过依次考察点集中的点,找出极值点,利用极值点快速形成初步凸包.初步凸包把原点集中的点分为初步凸包上点、外部点和内部点3个部分.外部点可能在凸包上,而内部点一定不在凸包上.算法的第2步则是删除内部点.第3步依次进行考察外部点,不断扩展初步凸包,最终形成所要得到的凸包.在扩展初步凸包的过程中,将待考察的点依次与上一步扩展凸包中的棱边构成面,并用极值点和上一步扩展凸包中的顶点集中的点判断该面是否应加入新的扩展凸包中,这样就可以找到所有应加入新扩展凸包中的面.再利用该待加入点和极值点验证原扩展凸包中的面,排除不满足新扩展凸包的所有的点、棱边和面.当考察完毕所有外部点时就可以得到最终所要求得凸包的点集、棱边集和面集.
2.1 算法主体流程
算法主体流程见图1.

图 1 算法主体流程
2.2 算法具体步骤
步骤1 求极值点并形成初步凸包,分为4个小步骤进行.
(1)依次考察点集中点的z坐标,分别求出1个最大和1个最小的一维极值点,并把点号保存在极值点集链表utdot中.
(2)依次考察点集中点的x坐标和y坐标,按照左下点、下左点、下右点、右下点、右上点、上右点、上左点和左上点的顺序依次求出所有存在的二维极值点,并将点号保存到极值点集链表utdot中.
(3)按照求取二维极值点的顺序,依次连接各点构成1个空间环;然后将z轴方向上的极值点分别与环中的点连接,构成基于三角形初步凸包.
(4)在步骤1的第(3)步中,把依次连接的边保存到棱边集链表llist中,把依次连接3点构成的面保存到面集链表alist中.同时,初始化顶点集链表endplist后,继续下一步.
步骤2 删除初步凸包内部点,又分为2个小步骤进行.
(1)依次考察点集中的点,从该点出发引1条平行于x轴的射线,如果该射线与初步凸包的面不相交或有2个交点,则该点在初步凸包的外部;如果只有1个交点,则该点在初步凸包的内部.如果与初步凸包的棱边、面或顶点相交,则改平行于y轴或z轴的射线,然后再按照前面的方法判定.如果3个方向的射线均与初步凸包的顶点或棱边相交,则该点在初步凸包的内部.[1]
(2)在步骤2的第(1)步中,把初步凸包外部点的点号保存到点集链表plist中.继续下一步.
步骤3 从点集链表plist中依次取出点pp,如果链表plist中点都取完,则执行步骤5,否则继续下一步.
步骤4 共有10个小步骤.依次从棱边集链表llist中取出棱边lp,如果链表llist中的棱边都取完,则执行步骤4中第(5)步,否则继续步骤4中第(1)步.
(1)由步骤3中的点pp和步骤4中的棱边lp构成1个面,依次用极值点集utdot中的点来判断该面的性质.如果所有极值点都在该面的同一侧,则继续下一步,否则退出本轮循环,执行步骤4.
(2)从顶点集链表endplist中依次取出点来判断该面的性质,如果所有点都在该面的同一侧,则继续下一步,否则退出本轮循环,执行步骤4.
(3)把步骤4的第(1)和(2)步中满足要求的面加入到面集链表alisttemp中,与该面相应的两条棱边加入到棱边集链表llisttemp中.
(4)继续步骤4.
(5)若alisttemp为空,执行步骤4中第(10)步,否则执行下一步.
(6)依次从扩展凸包面集alist中取出面a,用点pp和极值点集utdot中不为该面顶点的1点putdot进行判断,如果点pp和点putdot在面a的异侧,则把该面从alist中删除,并且加入到待删除面集链表alistdle中,否则不作任何处理,继续步骤4中第(6)步.当alist中的面都取完时,把alisttemp添加到alist中,执行下一步.
(7)依次考察面集alistdle中的面,如果有3个或者以上的面相交1点,则把该点加入到待处理点集链表plistdle中,否则继续步骤4中第(7)步.当面集alistdle中所有点面都考察完毕时,执行下一步.
(8)依次考察点集plistdle中的点,如果该点在面集alist的顶点中不存在,则从顶点集endplist中删除该点,否则不作任何处理.当plistdle中所有的点都考察完毕时,把点pp添加到endplist中,执行下一步.
(9)依次考察面集alistdle中的面,如果有2个面相交于1条棱边,则从棱边集llist中删除该棱边.当alistdle中的面全部考察完毕时,把llisttemp添加到llist中,执行下一步.
(10)继续步骤3.
步骤5 把极值点集链表utdot合并到链表plist中.最终凸包的点集为链表plist,棱边集为链表llist,面集为链表alist.算法完成.
2.3 算法改进方法
上述算法利用z轴方向的2个一维极值点和xy平面上最多8个二维极值点形成初步凸包.根据定义3,x,y和z轴方向的一维极值点均分别在2个平面上.根据极值点的性质,所有一维极值点均为凸包顶点.所以改进的方法是:求出所有一维极值点并由其构成1个新初步凸包,这个新初步凸包大于等于上述算法中的初步凸包.新凸包可以排除更多的内部点,从而减少步骤3和4中的判断次数,提高算法效率.
2.4 时间复杂度分析
文献[7]证明凸包算法的时间复杂度下限为o(n logn),该结论也适用于三维凸包算法[1].常见的三维凸包算法中,卷包裹法和文献[1]中Z3—8算法的时间复杂度为o(n2)[1,6];分治法和增量法为o(n log n)[1].经典的普通算法是利用定义1的性质,通过3点构成的面,然后用点集中的点是否都在该面同一侧的方法来判断该面是否为凸包的面.当考察完毕点集中任意3点所构成的面时,就可以得到凸包的所有面,进而求出凸包.其算法的复杂度为o(n3).
本文算法的时间复杂度分析如下:步骤1中,查找极值点耗时o(n);步骤2中,删除内部点的复杂度为o(n);步骤3和4构成1个用外部点扩展初步凸包的循环.外部点的数目与点集的数目相关,故循环外部的复杂度为o(n).循环内部中步骤4的第(1)~(4)步求顶点与棱边构成的面,并用扩展凸包顶点集中的点判断面的性质,其复杂度与扩展凸包中点的数目和棱边的数目相关.由于扩展凸包中点的数目相对于点集中点的数目和棱边的数目非常少,也可以认为是常数.所以,一般情况下其计算的复杂度为o(1).由性质和推理知,极值点可以构成初步凸包,进而可以排除内部点.所以,即使在最坏情况下,其时间复杂度也不会达到o(n),可以认为其时间复杂度接近o(log n).步骤4的第(5)~(10)步的时间复杂度为o(1),所以步骤3和4的最坏时间复杂度接近o(n log n).步骤5耗时可以忽略不计.所以,整个算法的最坏时间复杂度接近于o(n log n),即接近于时间复杂度的下限.
3 实验分析
实验所用计算机的CPU为AMD 2500+,内存为512 MB.在VC++6.0中的MFC编程环境中,分别实现普通算法和改进算法.图2给出点集中点的数目为500个时的三维凸包计算结果.分别对普通算法和改进算法求三维点集凸包进行程序实验.对不同容量(小于104)的点集分别进行100次实验,然后求出平均消耗的时间列于表1和图3.同时,表1对普通算法和改进算法平均消耗时间的比值进行计算.图3中横轴表示点集中的数目,纵轴表示计算点集凸包运行所需要的平均消耗时间.

图 2 500个点的凸包计算结果
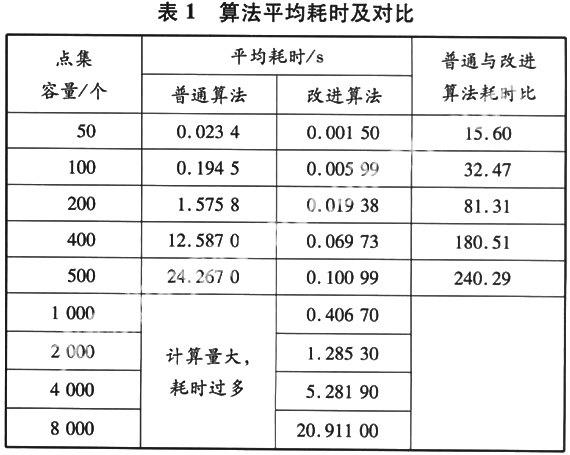

图 3 实验比较
从表1和图3可见,随着点集容量的增大,改进算法的优势越发明显.普通算法与改进算法的消耗时间比随着点集容量的增大而增大.在第2.4节中普通算法和改进算法的时间复杂度分别为o(n3)和o(n log n),它们之间的比值为o(n2/log n),与表1中的比值相符合,从而证明理论分析与实验分析一致.
4 结 论
从改进算法与普通算法的比较中可见,对于求102数量级的三维点集凸包,普通方法也能提供比较满意的求取时间,但当点集容量达到103时,普通算法就不能满足要求.改进算法可以快速求取大量三维点集的凸包,不仅在时间上取得较大突破,而且充分利用极值点在凸包上以及凸包的性质,为算法优化提供新的思路.
另外,改进算法效率高的原因还在于:(1)充分利用极值点,形成最大可能的初步凸包,排除初步凸包内部点,减少点的判断次数;(2)在判断面的性质中,优先用极值点进行判断,利用极值点的性质,可以很快得出该面的性质,减少判断的工作量;(3)在求取过程中,每次向扩展凸包中添加1个点,都构成1个新的扩展凸包,充分利用上一步中求取的成果,大大减少后面的计算工作量.
参考文献:
[1] 周培德. 计算几何——算法分析与设计[M]. 2版. 北京:清华大学出版社,2005:100-135.
[2] ROURKE O J. Computational geometry in C[M]. 2nd ed. Cambridge:Cambridge Univ Press,1998:73-78.
[3] 夏松,朱宜萱,杜志强. 一种新的空间凸多面体的生成算法[J]. 测绘通报,2006(1):21-23.
[4] 余翔宇,孙洪,余志雄. 改进的二维点集凸包快速求取方法[J]. 武汉理工大学学报,2005,27(10):81-83.
[5] 蒋红斐. 平面点集凸包快速构建算法的研究[J]. 计算机工程与应用,2002,38(20):48-49.
[6] 吴克勤,杨冠杰. 空间点集卷包裹算法的优化实现[J]. 青岛海洋大学学报:自然科学版,2003,33(4):627-633.
[7] YAO A C C. A lower bound to finding convex hulls[J]. J ACM,1981,28(4):780-787.
(编辑 廖粤新)

