多激励下舰船“声平衡”特性分析
姚熊亮 计 方
哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001
多激励下舰船“声平衡”特性分析
姚熊亮 计 方
哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001
以舰船流固声耦合理论为基础,基于势流理论,开发了工程化的舰船湿模态附连水质量三维计算程序,将计算值与理论值、经验值及有限元数值解进行对比分析,验证了程序的有效性和合理性。在此基础上,提出了一种计及流固耦合效应的舰船“声平衡”分析方法,研究了船—机—桨多点激励下船体—基座—设备间的耦合结构振动和水下声辐射。结果表明:舰船艏部自噪声随振源相对位置变化出现峰谷交替的趋势,通过优化主机位置可以降低艏部自噪声;舰船主辅机选型应充分考虑船体—基座—设备之间以及设备间的声匹配,兼顾多点激励力幅比和激励频率比。
舰船水声设计;总体声学性能;声平衡;水下辐射噪声;多点激励;耦合振动;附连水质量
1 引言
舰船减振降噪涉及众多学科,是一个十分复杂的课题,很难找到一类数学模型来表达一定物理状态下量(噪声)与量(舰船参数)之间关系的数学表示,一些经验公式也是在大量实测的基础上得到的。“单项好,总体差;陆地好,水中差”,总体声学性能不达标已经成为当前舰船声隐身技术发展的瓶颈。等舰船建造好以后再考虑其结构振动和水下辐射噪声问题,往往不能取得很好的效果。如果能够在舰船设计过程中对其予以考虑,从而修改舰船某些设计参数并提出切实可行的降噪方案,对降低舰船水下辐射噪声是十分有利的。
目前,国内外大多数有关这方面的研究工作都限于水下结构的振动和辐射噪声问题[1-4],仅仅注意了局部隔振、减振,忽视了总体声学性能匹配的问题。如对于动力设备的减振降噪,通常单独进行各个设备的减振处理,而忽略了各个设备之间的匹配问题。本文提出了一种舰船“声平衡”分析方法,研究船—机—桨多点激励下艇体—声学覆盖层—基座—设备间的耦合振动和由此形成的水下声辐射问题,这在研究方法和边界条件方面与以往的研究工作有较大的差别。本文讨论了不同激励下,通过改变不同激励力幅比以及激励频率比,考虑不同激励设备间匹配问题,优化选型,从而使舰船处于最优的“声平衡”状态。所谓“声平衡”状态,即综合考虑多个辐射亮点部位,使声辐射能量尽量沿船体均匀分布,使舰船艏部声呐舱自噪声最低,完善各设备减振降噪指标分解,使舰船的总体声学性能最优。
2 舰船流固声耦合理论分析
当舰体置于声学介质中时,流体与结构交接面上的流体与结构之间存在着相互作用,整个系统的研究成为一个舰体—流体—声场耦合振动问题。如果结构由有限元建模,对结构导出的运动微分方程为:

式中,{f}为结构载荷向量;[D]为正交变换矩阵;[E]是湿表面的对角面积矩阵,{p}为流体压力向量。假设所有压力、位移、速度都是和时间相关eiωt的函数,则式(1)可以写为:
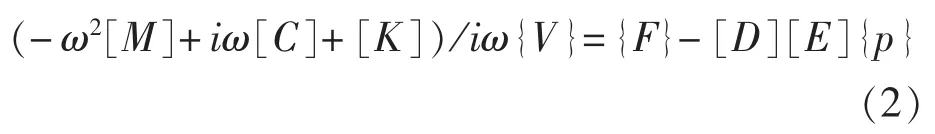
定义[Z]=(-ω2[M]+iω[C]+[K])/iω为结构的阻抗矩阵,则有:
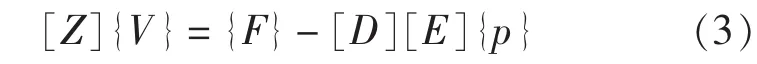
式中,{V}、{F}分别为结构速度向量、结构载荷向量的复数幅值向量;ω为圆频率,并且
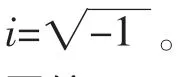
简谐激励作用下,结构振动在可压缩、无粘性、非流动的介质中产生的辐射声压波动方程。
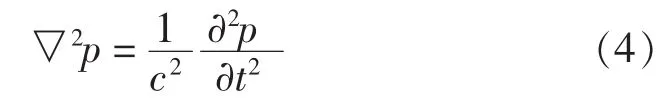
其中,p为瞬时声压;t为时间变量;▽2为拉氏算符,c为流体介质中的声速。在流固面S上,存在边界条件:

在无限远处满足Sommerfeld辐射条件。
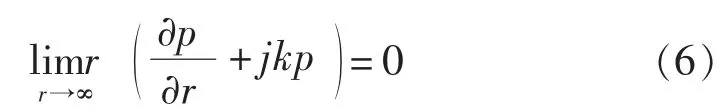
式(4)和式(5)、式(6)可以转化为单频声场的Helmholtz方程[5]。
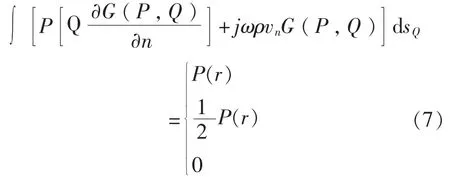
式中,E,S,I分别表示位置在结构外部,表面上和内部:Q为结构表面上的点,P为空间中的点;vn是边界表面的法向速度;n为结构表面外法向单位矢量;k=ω/c为波数;S为声源表面。
对式(7)利用边界元法进行离散,即可得到边界元求解方程。
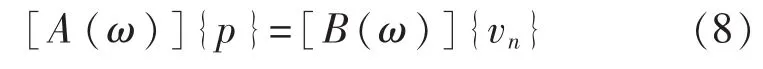
式中,[A(ω)]和[B(ω)]分别表示边界元法系数矩阵,{vn}为节点法向速度向量。得到表面压力后,结构表面上节点处的声强可由下式表示:
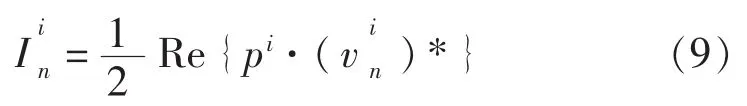
对式(9)作面积分即可得到结构声辐射功率。
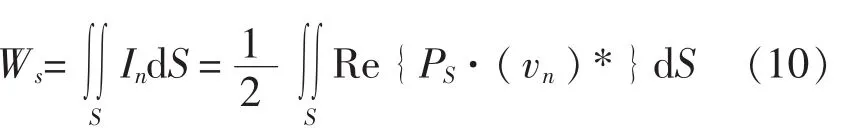
3 舰船附连水质量工程化计算
当舰船在运动时,环绕在船体周围的水也处于运动状态,因而舷外水对舰船的振动产生很大的影响,它的影响可以分为以下3个方面:重力的影响、阻尼的影响和惯性的影响。惯性的影响反映在参与船体振动的等效质量的改变。舰船是漂浮在水面上的,其剖面不是圆形或椭圆形的,同时船体也不是无限长的,因而其周围的流体运动是三维流动,这些都会对船体的附加质量产生影响。
舰船湿模态附连水质量计算精度直接影响舰船多激励下结构振动与声辐射数值预报的有效性,正确计算舰船附连水质量是关系到舰船水下辐射计算的关键技术之一。本文基于势流理论,采用BEM方法[6-9],开发了附连水质量三维计算程序,并将其工程化,计算舰船各阶湿模态的附加质量。
3.1 程序验证
一般的水下结构物均为刚体运动和弹性体振动的耦合系统,因此如何将刚体运动和弹性体振动进行耦合成为本文的核心问题。本文将刚体运动视为固有振型矩阵中每一个元素均为1的弹性体振动某一阶固有模态,定义其为0阶模态。在计算舰船附加质量之前,分别将本文程序计算的刚体运动及弹性体振动附加质量与理论值对比分析。
3.1.1 刚性体
取圆柱体水中绕流模型作为刚体附加质量的计算模型,如图1所示。

图1 圆柱体边界元模型
从表1可以看出,用数值方法计算附加质量存在一定的误差,并且长度直径比越大,计算所得的附加质量越接近于理论值。这是因为选取的圆柱体模型有限长,而圆柱体水中绕流模型附加质量理论解是基于无限长直圆柱假设而得到的结论。因此,本文数值解有较高的精度,验证了用数值方法计算刚体附加质量的正确性和有效性。
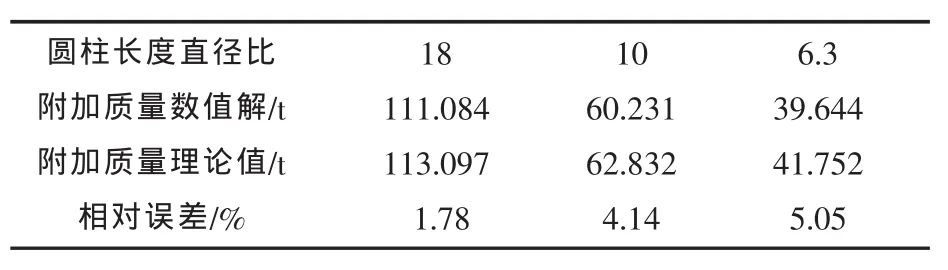
表1 刚体运动附加质量
3.1.2 弹性体
仍以圆柱体水中绕流模型为例计算弹性体振动附加质量的数值解,从而验证弹性体振动附加质量数值计算方法的正确性。但国军标是在直角坐标系下对附加质量进行估算,因此又需要将模态空间下的附加质量数值解转化到相应的物理空间下并和估算结果进行比较。
从表2可以看出,用边界元法计算弹性体振动附加质量数值解和估算公式结果有一定的差异,但在10%以内,说明本文的计算方法是可行的。另外,采用大型通用有限元计算软件Abaqus计算了直角坐标系下弹性体一阶振动附加质量,用数值计算方法计算弹性体一阶振动附加质量和有限元计算结果相当接近,再一次验证了该数值计算方法的有效性。
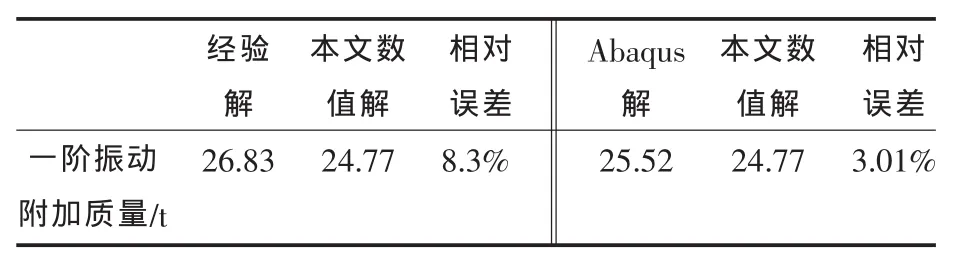
表2 弹性体振动附加质量
3.2 工程化舰船湿模态附加质量
在验证本文所开发程序有效性的基础上,分别计算了舰船刚体附加质量、弹性振动的附加质量及其二者的耦合附加质量,并分析了不同振型之间的耦合响应。表3给出了舰船直角坐标系下的附加质量。其中,分别表示舰体纵向、横向、垂向刚体运动,即0阶模态,1、2分别表示舰体一阶、二阶弹性自由振动,振动方向为舰体垂向。

图2 舰船水下部分边界元模型

表3 舰船湿模态附加质量(直角坐标)
从表3可以看出,舰体纵向平动附加质量很小,而垂向和横向平动附加质量很大,这是因为舰体横剖面面积要远远小于舰体纵剖面面积和水线面面积。另外,舰体垂向平动和纵向平动耦合附加质量相对纵向平动本身较大,而它们与舰体横向平动耦合附加质量均很小。舰体一阶振动和二阶振动附加质量很大,因为振动方向为舰体垂向。舰体一阶振动二阶振动耦合附加质量很大,因此该耦合项不能忽略。弹性振动方向与舰体横向平动耦合很小,与垂向平动耦合很大,与纵向平动耦合相对纵向平动本身较大,这与舰体水下部分几何形状有关。
表4分别给出了舰船一阶、二阶振动附加质量本文的数值解与经验解,其中,经验解为《中华人民共和国国家军用标准》给出的水面舰船附连水质量的经验公式(11)求得。

式中,mv为垂向振动时各计算剖面处单位长度上的附连水质量;αv为浅水修正系数;Ki为三维流动修正系数;Cv为附连水修正系数;ρ为海水密度;b为剖面水线处半宽。
从表4可以看出,本文数值解与经验解相对误差在5%以内,因其工作量小耗时短,具有较强的工程应用价值。
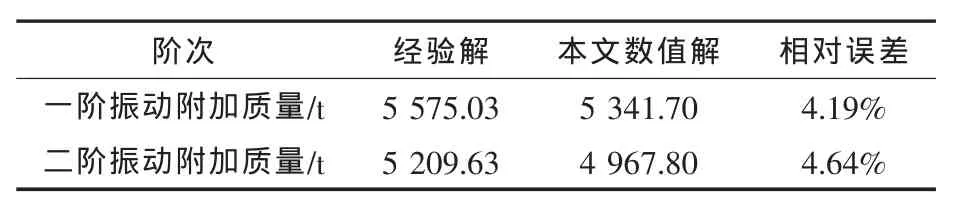
表4 舰船弹性振动附加质量比较
4 舰船多点激励
以往将机、轴、桨或者船体、基座、设备分别加以研究的方式不利于舰船减振降噪研究工作的深入,本文系统分析了船—机—桨多点激励下船体—基座—设备间的耦合振动和由此形成的水下声辐射问题。引起舰船振动和水下辐射噪声的主要激振力有:
1)由螺旋桨工作引起的螺旋桨叶频激振力(螺旋桨转速×叶片数,声场计算中等效为球面噪声源)。螺旋桨轴频激扰力主要是由建造质量引起的,舰船正常航行时轴频激扰力相对较小,叶频激扰力是螺旋桨激振力的主要成分。因此,本次计算中主要考虑了螺旋桨脉动压力与轴承力的影响。
2)主辅机产生的缸频激振力 (柴油机转速×气缸数)。柴油机激励力通常是简谐激励力,表5为柴油机生产厂家提供的舰船主辅柴油机不平衡力或力偶的幅值。
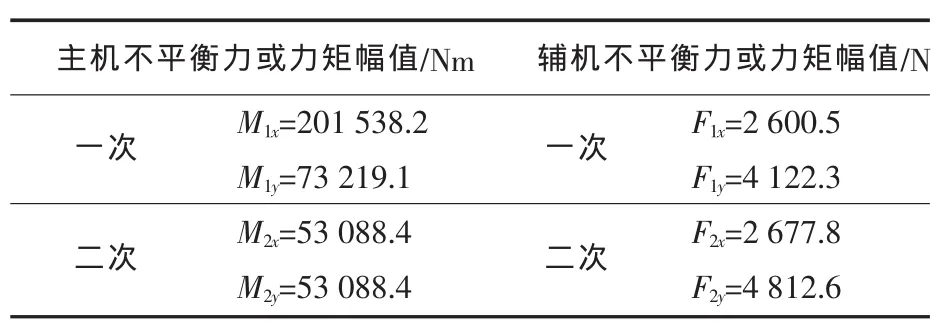
表5 舰船柴油机激励力
3)齿轮箱激励力[10](由不同频率下的加速度及齿轮箱的质量求出等效的惯性力作为其输入激励载荷)。
本文计算了3种激励情况下的水下辐射噪声,这3种激励情况为:
1)主机激励且设置不同的主机相对位置,即主机在额定转速下工作,而其它机械设备不工作且螺旋桨不运转;
2)主机、辅机共同激励并设置不同的激励比,即主机、辅机在额定转速下工作,而其它机械设备不工作且螺旋桨不运转;
3)全部激励,即主机、辅机、双机并车齿轮箱、螺旋桨同时激励,计算舰船在最大航速27 kn和巡航速度18 kn时的水下辐射噪声。
5 舰船“声平衡”分析
5.1 全激励下舰船声辐射特性分析
舰船辐射噪声和自噪声不仅和主辅机的类型密切相关,当讨论舰船的声源级和声压级数值时,必须指明航速与航行状态,才具有实际意义[11]。
图3给出了舰船巡航航速18 kn时的频谱图。从图中可以看出:舰船辐射噪声声源级的频谱是由连续谱和线谱叠加而成的混合谱。数值计算结果表明连续谱占有辐射噪声的绝大部分能量,舰船噪声的连续谱有一峰值,其谱峰频率为200 Hz左右,当超过这一频率时,频谱呈明显衰减趋势,每倍频程衰减约6 dB。
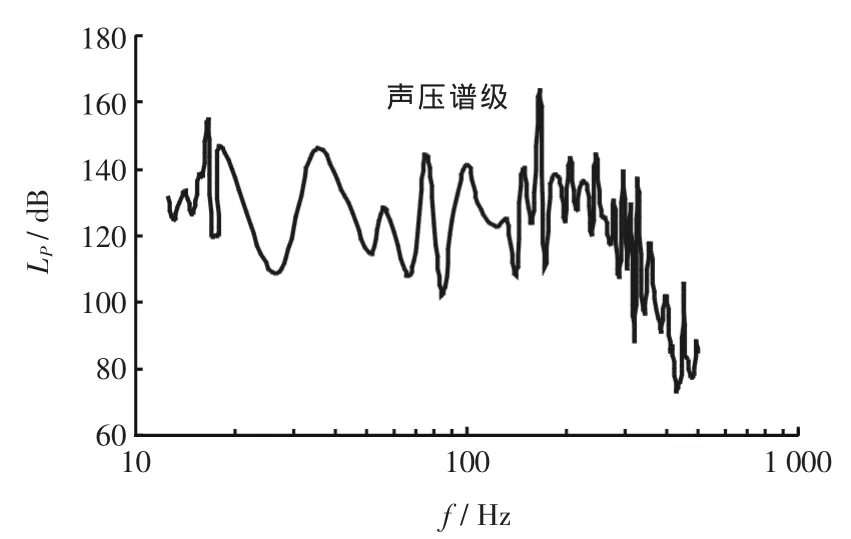
图3 舰船辐射噪声频谱图
不同激励情况下的水下辐射声压计算结果列于表6中,表中所列的声压级数值是换算到距离舰船等效声中心1 m处的声压级,即声源级。
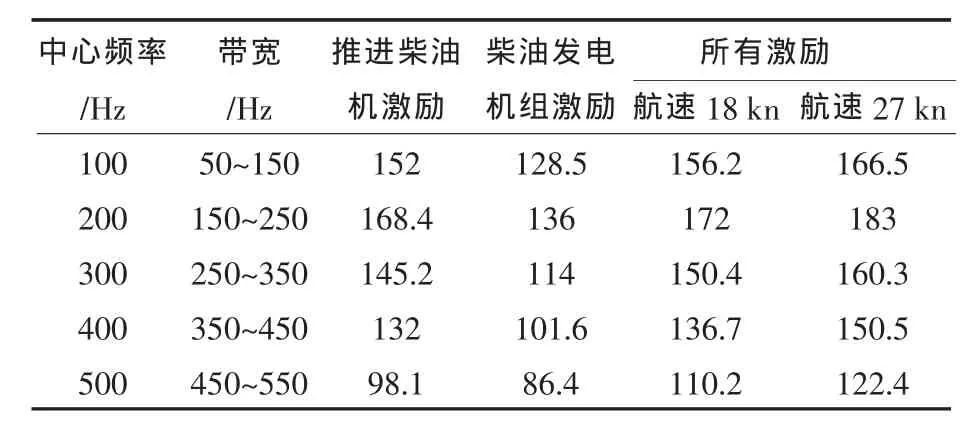
表6 不同激励下水下辐射噪声声压级LP(i)(dB)
表6中计算了仅考虑推进柴油机激励、柴油发电机组激励情况下的舰船水下辐射噪声,并对考虑所有激励力时的舰船水下辐射声压进行了数值计算。当然,实际舰船航行时不可能出现仅推进柴油机、柴油发电机组或双机并车齿轮箱工作,而其它设备不工作的情况。但前述的计算结果可为确定引起舰船水下辐射噪声的主要激励源提供依据。从表6中可以得出如下结果:
1)在50~550 Hz频率范围内,对于推进柴油机激励、柴油机发电机组激励情况下,从各个中心频率的总声压级比较可知,推进柴油机激励引起的舰船水下辐射噪声比柴油机发电机组激励引起的水下辐射噪声大得多。这表明,尽管推进柴油机安装有隔振器减振,但它仍然是产生舰船水下辐射噪声的主要声源。
2)在50~550 Hz频率范围内,舰船航速从18 kn增加到27 kn时,对应于各中心频率的水下辐射声压分别增加 10.3 dB、11 dB、9.9 dB、13.8 dB、12.2 dB。主要原因是由于舰船航速在巡航速度18 kn时,推进柴油机并不在最大工况下工作。
5.2 舰船艏部声呐区“声平衡”特性分析
舰船声呐阵大都布置在艏部,若能有效降低艏部自噪声,则本舰声呐探测敌方目标的距离将增加。所以,研究激振力位置对舰艏自噪声的影响具有重要意义。
图4给出了舰船航速18 kn全激励下自噪声沿船体分布曲线。可以看出:主辅机位置对应自噪声的峰值,舰艏、舯、艉对应自噪声的波谷。自噪声沿船体的分布除与激励密切相关,还与内部机械布置、噪声传播途径有很大关系。全激励下自噪声沿船体的分布可为查找噪声源、设计舷侧声呐阵等提供依据。
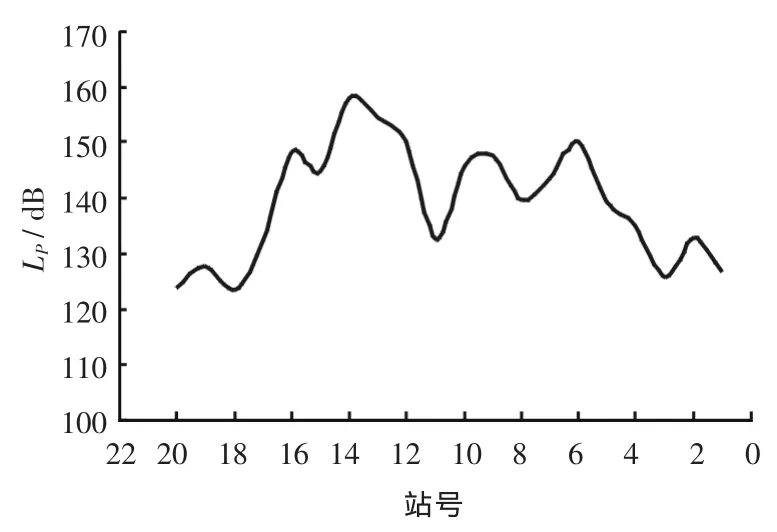
图4 舰船18 kn下自噪声沿船体分布曲线
图5、图6给出了某激励频率下,在不同主机相对位置激励时,所得到的舰船铅垂声压分布图(限于篇幅只给出部分图形)。其中,l为振源到船艏部距离;L为船长。从图中可以看出,不同部位激振时,辐射声压呈花瓣状分层向外辐射,70%部位激振时辐射声压级明显小于55%部位激振。
图7为艏部自噪声随主机相对位置变化曲线。可以看出,舰船艏部自噪声随振源相对位置变化出现峰谷交替的变化趋势,并非振源离舰艏部越远,艏部自噪声越小。不同频率下70%、80%部位激振时,艏部自噪声处于波谷,而75%部位激振时,艏部自噪声处于波峰。20 Hz、100 Hz、200 Hz激励时舰船艏部声压级峰谷最大差值为14 dB、12 dB、5 dB;不同频率下70%部位和75%部位激振时的艏部声压级差值分别为4 dB、10 dB、4 dB。由此可见,可以通过优化主机相对位置降低艏部声呐区自噪声。另外也可以看出,当振源出于90%位置时,舰船艏部自噪声也比较小,因此,也可以通过舰船尾部吊舱推进,使艏部自噪声最低。

图5 l/L=55%部位激振铅垂声压分布图

图6 l/L=70%部位激振铅垂声压分布图

图7 艏部自噪声随主机相对位置变化曲线
5.3 舰船主、辅机“声平衡”特性分析
从“声平衡”角度出发,讨论不同激励下,通过改变多点激励力幅比以及激励频率比,考虑主、辅机的匹配问题,优化选型。图8~图10给出了主、辅机激励力幅之比分别为1~5的自噪声声压等值图(限于篇幅只给出部分图形)。从图中可以看出:当激励比为1时,舰体自噪声主要在主辅机激励位置以及舰体中部较大,而其他部位声学响应较小;随着激励比增加至4时,舰体自噪声声压值也逐渐增大,且声辐射能量同样主要集中在激励位置以及舰船中部位置处;而当激励比增加至5时,舰船自噪声沿船长分布更加均匀,且声压级幅值下降较大,变化趋势复杂。由此可见,在进行主辅机选型时,应充分考虑到舰船结构本身的特性,避免能量集中辐射,尽量使噪声辐射能量沿船长均布分散,从而降低舰船水下辐射噪声。

图8 主辅机激励之比=1时自噪声声压等值图

图9 主辅机激励之比=3时自噪声声压等值图

图10 主辅机激励之比=5时自噪声声压等值图
图11给出了不同激励下,舰船自噪声沿船长的分布情况。从图中可以更直观地看出,通过声平衡分析,当激励比为5时,舰船自噪声沿船长分布更加均匀,减小了亮点辐射,使舰船噪声能量沿船长均匀分布,从而降低舰船水下辐射噪声。
为进一步分析舰船水下声辐射特性,图12、图13给出了主辅机在不同激励力幅比时,舰船辐射声源级和辐射声功率曲线。从图中可以看出二者呈现相似的变化规律,在100 Hz和200 Hz附近出现峰值。声源级和辐射声功率级的幅值在主辅机激励比为1时最小,随着激励比的增加而增加,在激励比为4时最大,200 Hz共振峰处二者幅值的最大差值约20 dB。而当激励力幅比继续增大,声源级和辐射声功率级的幅值显著降低,低频段甚至较激励比为1时效果更好。
舰船水下辐射噪声不仅取决于其表面的振动幅值,还与以振动能转移到周围水介质的能力密切相关。为了衡量结构的声辐射能力,图14给出了不同计算工况下舰船声辐射效率曲线。从图中可以看出:当激励力幅比为4是辐射效率最大,表明有较大部分的振动能转化为辐射声能。当激励比等于1和5时辐射声源级和声功率级的幅值较小,且激励比为5时辐射效率最小。因此,在主辅机选型时应充分考虑不同激励力幅下的舰船水下噪声辐射情况,以降低舰船的水下声辐射。
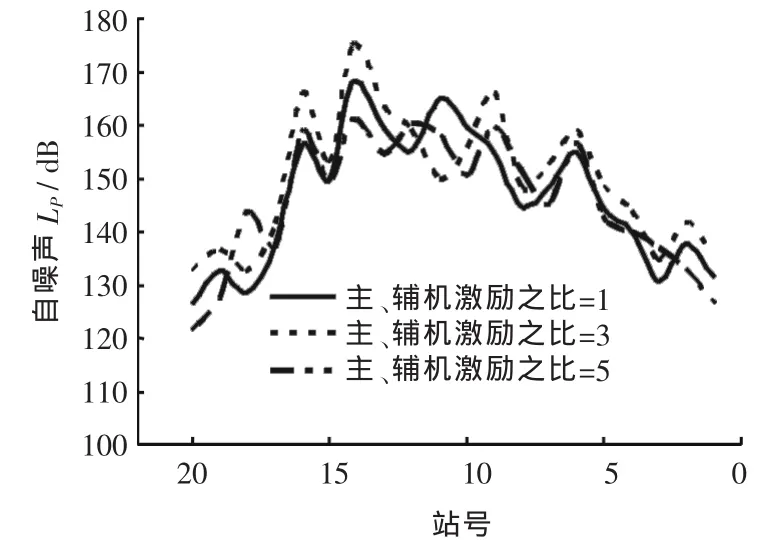
图11 不同主辅机激励下舰船自噪声沿船长分布
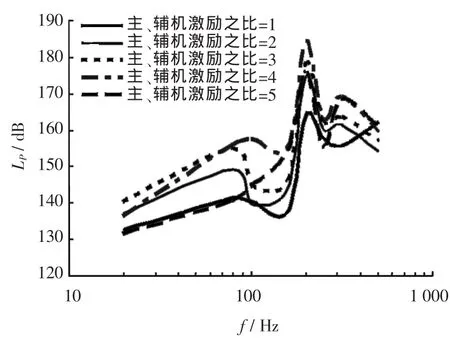
图12 不同主辅机激励下频带声源级曲线
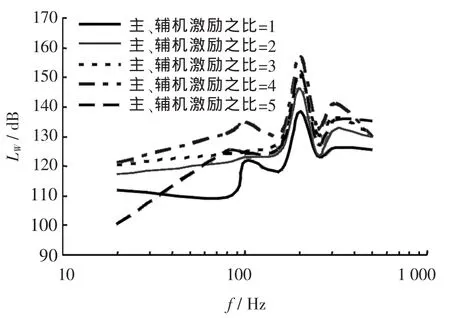
图13 不同主辅机激励下辐射声功率曲线
图15给出了不同频率下,舰船辐射声源级随主辅机激励力幅比的变化曲线。图中表明:不同频率1/3倍频程的频带声源级随主辅机激励力幅比增加呈现不同的变化规律。各频带声源级在不同激励比下最大差值15 dB,最小为5 dB,且最优激励力幅比不尽相同。因此,主辅机的选型既要考虑降低全频段的声源级,同时又要兼顾协调舰船机械设备运转的主要频带,合理进行舰船“声平衡”频带优化。
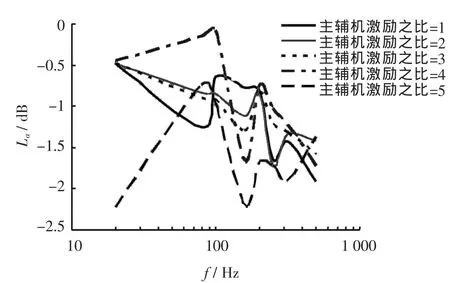
图14 不同主辅机激励下声辐射效率曲线
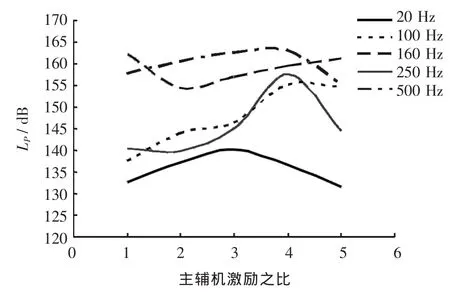
图15 声源级随主辅机激励比变化曲线
以上对舰船水下噪声的分析是假定主辅机的激励频率相同时得到的。然而舰船的主辅机的额定转数、气缸数都不相同,下面讨论主辅机激励频率比对总声源级的影响。图16给出了舰船噪声辐射声源级随主辅机激励频率比变化曲线。可以看出:不同激励力幅下,声源级随不同激励频率比呈现出峰谷交替变化趋势,当主辅机激励频率之比为3/5时,辐射噪声声源级处于波谷位置。
综上所述,主辅机选型的声匹配问题,应从舰船结构角度出发,既要考虑激励力幅比,又要兼顾激励频率比;既要考虑全频段的综合效果,又要兼顾主要工作频带,从而最大程度地降低舰船水下声辐射。

图16 声源级随主辅机激励频率比变化曲线
6 结论
1)舰船垂向平动附加质量大于舰体一阶振动附加质量,而一阶舰船振动附加质量又稍大于二阶舰船振动,三者相互耦合附加质量也很大,不能忽略;
2)舰船艏部自噪声随振源相对位置变化出现峰谷交替的变化趋势,并不是振源离舰艏部越远,艏部自噪声越小,而是有一个最佳的匹配位置,可以通过优化主机位置降低艏部声呐区自噪声;
3)舰船结构声学设计应充分考虑各动力设备之间的声匹配特性,通过主辅机优化选型,避免能量集中辐射,尽量使噪声辐射能量沿船长均匀分布。
[1] ZINOVIEV A,BIES D A.On acoustic radiation by a rigid object in a fluid flow[J].Journal of Sound and Vibration.2004,269(3-5):535-548.
[2] 邹春平,陈端石,华宏星.船舶结构振动特性研究[J].船舶力学,2004,7(2):102-115.
[3] TONG Z,ZHANG Y,ZHANG Z,et al.Dynamic behavior and sound transmission analysis of a fluid-structure coupled system using the direct-BEM/FEM [J].Journal of Sound and Vibration,2007,299(3):645-655.
[4] 陈美霞,骆东平,王祖华,等.激励力对双层圆柱壳声辐射性能的影响[J].船舶力学,2005,9(2):124-130.
[5] SEYBERT A F,WU T W.Modified Helmholtz intergral equation for bodies sitting on an infinite plane[J].J Acoust Soc Am,1989,85(1):19-23.
[6] ZHAO Z G,HUANG Q B,HE Z.Calculation of sound radiant efficiency and sound radiant modes of arbitrary shape structures by BEM and general eigenvalue decomposition[J].Applied Acoustics,2008,69(9):796-803.
[7] ZILMAN G,MILOH T.Kelvin and vlike ship waves affected by surfactants[J].J Ship Res,2001,45(2):35-44.
[8] CHEN X B,DUAN W Y.Capillary-gravity waves due to an impulse disturbance[C]//Pro.18th Intl Workshop on Water Waves and Floating Bodies, Carry-Le-Rouet France,2003.
[9] CISKOWSKI R D,BREBBIA C A.Boundary element in acoustics[M].WIT Press,2000.
[10] ZHOU Q,JOSEPH P F.A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J].Journal of Sound and Vibration,2005,283(3-5):853-873.
[11] 王之程,陈宗岐,于沨,等.舰船噪声测量与分析[M].北京:国防工业出版社,2004.
Characters of Sound Balance from Multi-support Excited Ship Hull
Yao Xiong-liang Ji Fang
College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China
Based on the theory of ship fluid-structure-sound coupling interaction,the engineering three dimensional program was explored to compute the entrained water mass of ship wet mode on the basis of Potential Flow Theory.The calculated results were compared with the theoretical value,empirical value and numerical value of FEM to verify the validity and rationality of the program.A method of“sound balance”was proposed to analyze the coupling vibration of hull-base-equipment which is excited by ship-equipment-paddle as well as underwater sound radiation.The results show that the sound pressure of stem with engine location takes on peak-to-valley tendency,which can be reduced through the optimum matching site.As for the selection of ships'main and auxiliary engines,the sound balance of hullbase-equipment as well as that of equipment needs to be considered,and this method must give attention to multi-support excitation force ratio and the frequency ratio.This article aims to provide reference for acoustic design of hull structure.
ship acoustic design;general acoustic performance;sound balance;underwater radiation noise;multi-support excitation;coupled vibration;entrained water mass
U661.44
A
1673-3185(2009)05-01-07
2009-03-05
国防重点预研项目;国际科技合作项目(2007DFR80340);高等学校博士学科点专项科研基金(20070217074)
姚熊亮(1963-),男,教授,博士生导师。研究方向:船舶与海洋工程结构动力学。E-mail:saibei8411@163.com
计 方(1984-),男,博士研究生。研究方向:船舶结构振动及噪声控制

