一种电子地图最短路径算法研究

王　昊

[摘要]针对最短路径算法在电子地图领域的运用，分析、实现并验证Dijkstra算法在该领域运用的可行性。还指出Dijkstra算法的不足，以及解决思路。

[关键词]电子地图 最短路径 算法

中图分类号：TP3文献标识码：A文章编号：1671－7597（2009）0310066－02

一、引言

所谓最优路径是指网络两个结点之间阻抗最小的路径。最短路径分析是地理信息系统网络分析中的基本功能，在很多领域应用十分广泛。最短路径分析以路径网络为基础，用户通过给出起点和终点，并赋予一定的权值，可得到从起点到终点的最短路线图。通常的最短路径算法往往是建立在抽象的数学模型之上。在网络模型上，实际的路径被抽象为网络中的一条边，实际路径的长度与网络边的长度可以不成比例，以边的权值来表征路径的长度，在该网络上求某点到其它任一点的最短路径的方法，被称为最短路径算法。Dijkstra算法是目前多数系统解决最短路径问题采用的理论基础。不仅可以找到最短的路径，而且可以给出从起点出发到图中所有节点的最短路径，这正是此种算法的特色。

二、Dijkstra算法

（一）算法的基本思想

基本思想：设置一个顶点的集合s，并不断地扩充这个集合，一个顶点属于集合s当且仅当从源点到该点的路径已求出。开始时s中仅有源点，并且调整非s中点的最短路径长度，找当前最短路径点，将其加入到集合s，直到终点在s中。

（二）算法原理

Dijkstra算法将网络节点分为未标示节点、临时标示节点和已标示节点3种类型。开始网络搜索时，所有节点首先初始化为未标示节点，在搜索过程中和最短路径节点相连通的节点记为临时标示节点，每一次循环从临时节点找到的距源点路径最短的节点记为已标示节点，直到找到目标节点或者所有节点都成为已标示节点为止。下面是该算法的描述。

1．用带权的邻接矩阵Cost来表示带权的n个节点的有向图，Cost[i，j]表示弧的权值，如果从vi到vj不连通，则Cost[i，j]=∞。图1表示了一个带权有向图以及其邻接矩阵。

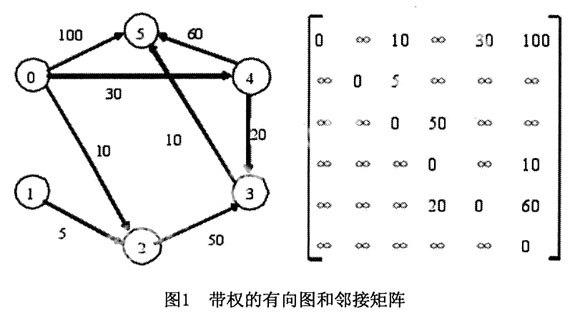
然后，引进一个辅助向量Dist，每个分量Dist[i]表示从起始点到每个终点vi的最短路径长度。假定起始点在有向图中的序号为i0，并设定该向量的初始值为：Dist[i]=Cost[i0，i]，vi∈V。令S为已经找到的从起点出发的最短路径的终点的集合。

2．选择Vj，使得Dist[j]=Min{Dist[i]|Vi∈V-S}，vi∈V。Vj就是当前求得的一条从vi0出发的最短路径的终点，令，S=S∪{vj}。

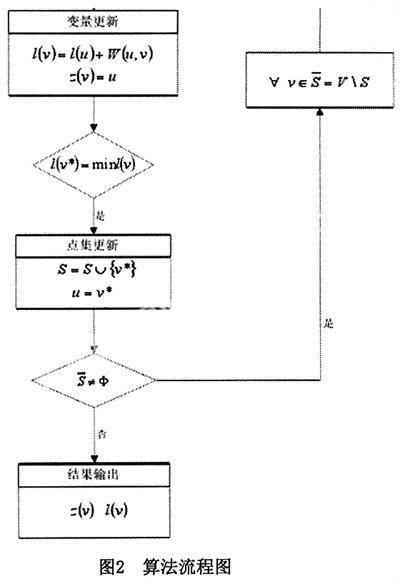
3．修改从vi0出发到集合V-S中任意一顶点vk的最短路径长度。如果Dist[j]+Cost[j，k]

[j,k]。

4．重复第2、3步操作共n-1次，由此求得从vi0出发的到图上各个顶点的最短路径是依路径长度递增的序列。

在应用中，采用Dijkstra算法计算两点之间的最短路径和求从一点到其它所有点的最短路径所需要的时间是一样的，算法时间复杂度为O（n2）。

（三）算法步骤

设带权图表示为G=，其中，V是图中顶点的集合，E是边的集合，W是相应的边的权的集合。

设带权图G=是n阶简单带权图，W(Vi，Vj)大于等于零（即第i条边的权大于等于零），若顶点Vi与Vj不相邻，则令W(Vi，Vj)=∞，求G=中Vo到其余各个顶点的最短路径。

设L是G中的一条路，把路L上带权总和称为L的权和，记为|L|，又设P(G)是权图中所有顶点的集合，S是其中某些点组成的集合，u0是S中的一个点，S=P(G)S，把从u0出发到S中点的具有最小权和的路径称为u0到S的距离，记为d(u0,S)，从而求出u0到其余顶点的最短路径。

（四）算法的瓶颈

在原始Dijkstra算法的过程中，核心步骤就是从未标记的点中选择一个权值最小的弧段，这是一个循环比较的过程，若不采用任何技巧，未标记点将以无序的形式存放在一个链表或数组中。则要选择一个权值最小的弧段就必须把所有的点都扫描一遍，在大数据量的情况下，是一个制约计算速度的瓶颈。

三、Dijkstra算法的程序实现

（一）基本思路

采用树生长的过程来求指定顶点到其余顶点的最短路。设G为赋权网络有向图，权值即为边的长度。该算法是求G中从顶点u0到其余各点的最短路。

S：已知最短路径的顶点集。对每个顶点，定义两个标记（l(v),z(v)），

其中：l(v)：表示从顶点u0到v的一条路的长度。z(v)：v的父亲点，用以确定最短的路线。

算法的过程就是在每一步改进这两个标记，使最终l(v)为从顶点u0到v的最短路的长度。输入为长度值邻接矩阵ω(U,V)。u：起点标号；v：终点标号。程序中的u和v是两个变量，不断被赋予新值。

算法流程图如图2所示。

（二）程序代码

算法流程分析的是从固定顶点u0到其余各点的最短路，而作者要解决的是从任意顶点m到任意顶点n的最短路，本质算法并不改变，只是针对不同的m选取不同的u0，再从一组计算结果中选取l(n)和z(n)即可。

Dijkstra函数带有一个字符串型的参数，用来表示传递数组名matrix_name，二维数组matrix()经过多次迭代，最终得到m点到其它各点的最短距离，这些距离值构成数组l(i)，所要求m到n的距离即求出l(n)。代码如下：

Private Function Dijkstra(matrix_name As String)；Dim s(50)As Single；Dim u,v As Single；Dim matrix

()As Double；ReDim matrix(pNum,pNum)；'如果数组名为path_noright，调用该数组'；If matrix_name="path_noright"Then；For i=LBound(path_noright)To UBound(path_noright)；For j=LBound(path_noright)To UBound(path_noright)；matrix(i,j)=path_noright(i,j)；Next j；Next i；'如果数组名为path_right，调用该数组'；ElseIf matrix_name="path_right"Then；For i=LBound(path_right)To UBound(path_right)；For j=LBound(path_right)To UBound(path_right)；matrix(i,j)=path_right(i,j)；Next j；Next i；End If；'获取m行的值，保存在l()中'；For i=0 To pNum；l(i)=matrix(m,i)；z(i)=m'z()中保存到达终点的前一个点；Next i；s(0)=0；u=s(0)；k=0；Do While ks(j)Then；If l(i)>l(u)+matrix(u,i)Then；l(i)=l(u)+matrix(u,i)；z(i)=u；End If；End If；Next j；Next i；Dim ll(50)As Double；For i=0 To pNum；ll(i)=l(i)；Next i；For i=0 To pNum；For j=0 To k；If i<>s(j)Then；ll(i)=ll(i)；Else；ll(i)=1E+38；End If；Next j；Next i；Dim lv As Double；lv=1E+38；For i=0 To pNum；If ll(i)

四、结束语

本文分析并总结了Dijkstra算法的思路与编程实现过程，验证了其在虽短路径算法上的优势和不足之处，证明其在电子地图上运用所具有的优势，得出Dijkstra算法在电子地图等领域运用的宽广前景。

参考文献：

[1]董涌江，GIS网络分析功能的实现[J].三晋测绘，2003,12(2):89～92.

[2]邬伦、刘瑜、张晶等，地理信息系统的原理、方法和应用[M].科学出版社，2001,4～20.

[3]赵静、但琦、严尚安等，数学建模与数学实验[M].高等教育出版社，2000,15～24.

[4]鲍培明，距离寻优中Dijkstra算法的优化[J].计算机研究与发展，2001,3(1):76～79.

[5]张贵军、吴惕华，GIS线形矢量图形最优路径算法研究及仿真实现[J].系统仿真学报，2003,4(3):7～9.

作者简介：

王昊，男，汉族，北京人，学历本科，湖北交通职业技术学院，助理讲师，研究方向为算法设计。