ＳＤＮ供需流的两阶段及其优化分析

何建佳　徐福缘

[摘 要] 在传统企业向供需网企业转变过程中,作为SDN的一个供需流,其核心集中在对车间生产调度及物流配送的优化上｡针对这两个问题,基于木地板生产企业的现状,本文引入了量子粒子群与模拟退火相结合的混合算法,以及一种求解物流系统的整合优化模型与求解的启发式算法分别对其进行研究,具有一定的实用价值｡

[关键词] 企业供需网;量子粒子群算法;整合优化;启发式算法

[中图分类号]F270.7;F273.7[文献标识码]A[文章编号]1673-0194(2009)03-0046-03

0 引 言

多功能开放型企业供需网(Supply and Demand Network with multi-function and opening characteristics for enterprises,SDN)是指以全球资源获取､全球制造､全球销售为目标,相关企业之间由于“供需流”的交互作用而形成的一种多功能的开放式的供需动态网络结构[1]｡因其具有网络性､多功能性､开放性和动态稳定性等特性[1-2],近些年来日益受到学术界和企业界的关注｡供需网理论符合了当今环境对企业的要求,也符合当今企业发展的需要｡因此,积极推动我国传统企业向供需网企业的转变对于企业成长与发展､提高企业质量及推动我国市场经济的健康发展都具有十分重要的现实意义｡推动我国传统企业向供需网企业的转变,其前提条件要求供需网系统本身具有一定的稳定性,这样才能满足供需网节点企业的多样需求｡而供需网稳定性的首要基础是供需网中供需流的稳定性,只有供需流在一定时期内处于稳定态才能保障供需网的状态稳定､相对稳定､波动稳定､动态稳定和有效稳定,即供需网处于稳定态｡

基于此,笔者就供需网中供需流的稳定性作出一些探索｡本文主要基于供需流的初始流及过程流的优化展开,当前推动我国传统企业向供需网企业转变的一个核心工作就是如何推动我国加工､制造企业向供需网企业的转变,而这类企业供需流的核心问题就集中在车间生产调度及产品配送上,这直接影响着SDN企业与上游原料供货商､各级分销商､终端客户的关系,从而诱发整个供需网系统的波动｡

1 SDN供需流的两阶段:调度与配送

作为供需网中的一个供需流,其核心主要涉及两个阶段(或说问题)——车间生产调度与物流配送｡其中物流配送又涉及车辆调度问题与车辆装载问题,二者相互影响､相互制约｡就木地板生产企业而言,车间调度实际上构成了一个典型的无等待流水车间调度(no-wait flow shop,NWFS)问题,这是流程工业中常见的一类调度问题｡当前基于蚁群算法[3]､离散粒子群算法[4]､禁忌搜索[5]等智能优化算法虽已比较成功地应用到NWFS的求解,但在实际应用中还是会陷入局部最优解,即出现不向最优解方向进化的早熟现象｡基于此,在实践的基础上,本文采用量子粒子群与模拟退火相结合的混合算法对无等待流水车间调度进行了研究｡量子粒子群算法,由于其涉及的参数少,编程上更易于实现,同时求解速度更优[6];而模拟退火算法是一种属于概率分布机制的优化算法,在搜索的过程中有一种时变且最终趋于0的概率突跳性,可以有效地避免陷入局部最优值最终趋于全局最优[7]｡

在物流配送上,学术界一般将车辆调度问题(Vehicle Scheduling Problem,VSP)抽象为线路安排或车辆线路问题,在其优化求解上多采用启发式算法､神经网络法､模拟退火算法等;在车辆装载问题(Vehicle Filling Problem,VFP)方面,一般将其视为三维装箱问题,理论上属于NP-完全问题,有限时间内难以找到问题的最优解｡同时,对这一问题的研究,往往基于对VSP或VFP问题的单方面展开,而将VSP与VFP统一起来考虑的研究很少｡显然对于企业供需网而言,作为供需网中的一个供需流,VSP和VFP问题是同等重要的两个命题,二者相辅相成,缺一不可,一个环节出问题势必会影响另一个环节,最终导致整个供需流的波动;同时这也与供需网的理念相违背,供需网强调的是整个系统的协同优化｡因此,将VSP与VFP 问题统一起来,对供需网的进一步研究就显得尤为重要｡

2 车间调度的优化

2. 1问题描述

木地板生产企业的无等待流水车间调度可以描述为n个工件要在m台机上加工完成,每个工件的加工顺序相同,每台机器加工的各工件的顺序也相同,且已知对应的加工的时间,一个工件一旦开始加工,其加工必须连续地完成,不允许等待｡要求得到与工艺约束条件相容的工件加工顺序,使得总的加工时间最短[8]｡在调度中还要满足以下假设:

(1)每一个工件同一时刻只能在一台机器上进行加工;

(2)同一时刻每台机器只能加工一个工件;

(3)不考虑工件加工的优先权;

(4)各工件必须按照工艺约束条件进行加工｡

与其他的调度相比,无等待流水车间调度相对比较简单,但是它仍旧是一个非常复杂和困难的组合优化问题｡

2. 2基于混合量子粒子群算法的流程设计及描述

量子粒子群算法作为一种随机搜索算法,在运行接近结束时容易陷入局部最优,因此遇到复杂的调度问题时就不能求得全局最优解,模拟退火使用概率来避免陷入局部最优,将二者结合的算法的具体流程如下:

(1)初始化算法参数(种群数目､退温速率､仿真次数､最大迭代次数);

(2)随机生成初始种群;

(3)计算各个个体对应的调度的目标值,种群中目标值最小的微粒为gbest,每个微粒的自身位置为pbest;

(4)判断算法是否到最大迭代次数,若是,转(8),否则转(5);

(5)根据进化方程产生成新的粒子;

(6)对种群中所有的个体均进行定步长抽样的模拟退火操作,以概率min[1,exp(-Δ/tk)]接受后代,及时更新pbest 和gbest;

(7)然后进行退温操作tk=λ·tk,λ∈(0,1),并返回到(4);

(8)输出该次仿真所得到的gbest;

(9)判断是否再次进行优化,若是,转(2),否则转(10);

(10)输出多次优化的统计结果,并结束算法｡

2. 3实例仿真

在此,为了测试算法的有效性,本文选择了Car类调度问题进行仿真研究,在Car类调度问题中粒子数为50,最大迭代次数为1 000,算例均进行20次仿真,仿真统计结果见表1｡

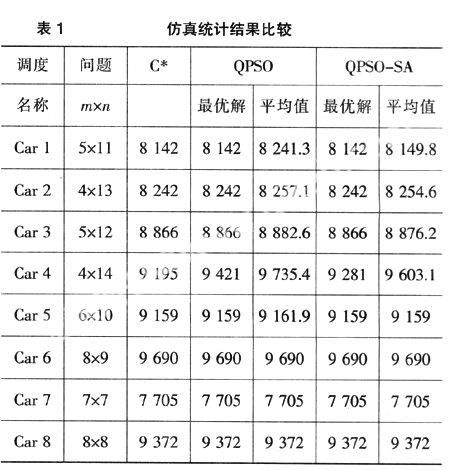
由表1的统计结果可知,在工件数比较小的调度中,量子粒子群算法和混合量子粒子群算法每次都可以求得最优解｡在机器数目多的调度中,也都能取得近似最优解｡从平均值来看,混合量子粒子群算法每次所取得的解要比粒子群算法取得的解要稳定,由此也说明了混合量子粒子群算法在搜索性能上具有更好的稳定性｡

3 物流配送系统整合优化的基本思想

将VSP与VFP 问题统一起来,其求解的关键,在于完成首次货物装载计算的同时,能随时正确和完全地反映出装载空间的变化情况(包括在各货点因不断进行上货或下货而引起的空间动态变化情况),且能得出新的配送装载方案｡因此,本文在基于有效空间的基础上给出以下思路:优先考虑VSP,在得出一个VSP的局部解之后,即进行相应的VFP求解,当验证其满足相应的约束并可行后,再回到VSP上进一步扩展已有的局部解,尔后再进行VFP求解､验证,如此反复,直到所有问题的解完｡

在算法设计上,本文采用基于VSP & VFP整合优化的启发式算法实现①,该算法的主体结构虽然还是分为VFP和VSP两大部分,但相互间联系密切,且互相影响｡

3. 1算法流程

由于整合模型的求解难度极大,加之模型所涉及的动态和不确定因素较多,故求解算法上分别在VSP和VFP的求解过程中特别设计了两个人工调控接口,用人工干预的方法来灵活控制,以提高整合模型可行解的几率和解的实际效果,具体如图1所示｡

3. 2程序设计

主程序主要基于Delphi 7.0配合桌面数据库Paradox来编制,程序的数据结构采用表结构,如:待装货物结构表､已装货物结构表､空间结构表等｡其主程序流程如图2所示｡

4 结束语

作为供需网的一个供需流,生产调度问题以及物流系统中的多车场､多车型､非满载､集送货一体化配送模式广泛的出现是当前影响我国传统企业向供需网企业转变的一个重要因素,特别是对于像木地板生产这类企业而言,生产及物流的整合优化对企业的成功转化及转化后的稳定性显得尤为重要｡因此,在生产调度及物流系统中,建立一个有效的优化模型并设计出相应的算法有着十分重要的意义｡

针对木地板生产企业的车间调度问题,本文将量子粒子群与模拟退火算法相结合,充分发挥各自算法的优势,并通过实例验证了混合量子粒子群算法解决无等待流水车间调度的可行性和有效性;针对物流配送问题,采用整合优化的思想｡这对于有效整合供需网企业中的节点企业(如木地板企业合理整合二级分销商等)､提高整个供需网的稳定性等都具有重要意义｡

主要参考文献

[1] 徐福缘,何静,等. 多功能开放型企业供需网及其支持系统研究——国家自然科学基金项目(70072020)回溯[J]. 管理学报,2007,4(4):379-383.

[2] 徐福缘,何静. 多功能开放型企业供需网初探[J]. 预测,2002(6):19-22.

[3] 潘全科,赵宝华,等. 一类解决无等待流水车间调度问题的蚁群算法[J]. 计算机集成制造系统,2007,13(9):1801-1815.

[4] 潘全科,赵宝华,等. 无等待流水车间调度问题的优化[J]. 计算机学报,2008,31(7):1147-1154.

[5] 刘佳佳,李小平,等. 一个求解无等待流水调度的混合算法[J]. 自动化技术与应用,2006,25(4).

[6] 石锦风,冯斌,等. 用带变异因子的QPSO算法解决Job-shop调度问题[J]. 计算机工程与应用,2008,44(8):49-52.

[7] 王凌. 车间调度及其遗传算法[M]. 北京:清华大学出版社,2003:85-86,102-103.

[8] LIU B,WANG L,JIN Y H. An Effective Hybrid Particle Swarm Optimization for no-wait Flow Shop Scheduling[J]. The International Journal of Advanced Manufacturing Technology,2007,31(9/10):1001-1011.

①当前流行的遗传算法对单独的车辆调度(VSP)求解效果虽比较满意,但与对应的车辆装载问题(VFP)结合显得较为困难;同时,尽管VFP部分具体应用时一般也可以采用遗传算法或启发式算法等加以实现｡但由于配送过程中车辆的货物装载情况是动态变化的,因此,这些算法也不再适用｡