基于DDA的膨胀土边坡破坏过程模拟
邱宽红,林绍忠,黄 斌
(1.长江科学院a.非连续变形分析实验室;b.水利部岩土力学与工程重点实验室,武汉 430010)
1 概 述
膨胀土是在自然地质过程中形成的一种多裂隙并且具有显著胀缩性的地质体,黏土成分主要由强亲水性矿物蒙脱石和伊利石组成[1]。膨胀土主要分布在干旱和半干旱地区,世界上许多国家都有膨胀土区域,我国膨胀土主要分布在西南和西北。随着我国西部大开发和工程建设的不断推进,遇到的膨胀土问题越来越多,发生了许多膨胀土地质灾害,造成了巨大的经济损失。
膨胀土边坡经过长期的气候风化和干湿循环作用,土体节理裂隙很多。裂隙的存在一方面破坏了土体的整体性,引起土体整体强度的降低;另一方面为雨水入渗和水分蒸发提供了良好的通道,气候对土体的影响深度进一步向土体内部发展。连续降雨引起的雨水入渗使得土体孔隙水压力上升,基质吸力减小,土体抗剪强度大幅度下降;并且土体吸湿后引起膨胀变形,由于各方向受到的约束不一致,从而增大剪应力,破坏土体的平衡,容易导致边坡失稳。从大量膨胀土边坡破坏的案例得知,即使膨胀土边坡比较平缓,但仍然发生了浅层滑坡。
2 膨胀土边坡稳定分析方法
膨胀土边坡稳定分析方法主要有刚体极限平衡法和有限元法。刚体极限平衡法是边坡稳定分析的常用方法,其原理简单,计算结果比较实用。制约极限平衡法计算结果可靠程度的因素主要有2方面:一是滑动面的位置和型式;二是滑动面抗剪强度的取值。对膨胀土边坡,滑动面型式主要有圆弧滑动型(顶部有垂直张裂缝)、滑动折线型和表层滑动型等。陈善雄[2]等采用滑动折线型,视土体为刚塑性材料,滑动面为3段折线型,采用竖向土条离散,土条间只有水平力作用,忽略剪切作用。有限元法物理概念清晰,适应性强(可考虑不同材料、复杂外形、环境变化、加固措施等),可以得到土体各点的变形以及应力应变信息,从而了解破坏区(塑性区)发生和发展的过程和范围。文[3]通过强度折减法对膨胀土边坡进行了稳定性分析,并且模拟了土工格栅加筋作用效果。
有限元法虽然可以模拟膨胀土边坡应力分布以及塑性区的发展,但不便于分析边坡的非连续变形和破坏过程。DDA能很好地分析非连续体的变形、破坏过程和稳定性,在岩土工程中应用广泛。对于土质边坡,文[4]用DDA进行强度折减计算,求得边坡的最小安全系数,文[5]用DDA模拟岩质边坡倾倒破坏过程,均取得了很好的效果。尽管如此,DDA在膨胀土边坡工程的应用还很少见。
3 DDA的基本原理与模型建立
3.1 DDA的基本原理
DDA平行于有限元法,块体切割类似于有限单元法网格划分,但所有单元是被事先存在的不连续结构面所包围的实际隔离体[6]。DDA中块体可以是凹块体也可以是凸块体,对块体形状没有要求。DDA具有完全的运动学及其数值可靠性、严格的平衡要求、正确的能量守恒和高计算效率,力学现象的数学和数值描述与块体运动相一致。
3.1.1 位移模式
大位移和大变形是由分步的小位移和小变形累加形成的。本文采用二维一阶DDA,即假设每个块体有常应力和常应变,块体形心点可用6个位移变量表示,

式中:(u0,v0)是块体形心刚体位移;r0为块体绕其形心的转动角;εx,εy,γxy分别是块体的正应变和剪切应变。
块体任意一点的位移为

式中,x0,y0是块体形心坐标。
3.1.2 平衡方程
平衡方程式用总势能最小化来建立,它是类似于有限元法的平衡方程。各个块体是通过块体间的接触弹簧和对单个块体的位移约束形成一个块体系统。假定有n个块体,联立方程有以下形式:

式中:Kii(i=1,2,…,n)为第 i个块体的刚度矩阵,Kij(i≠j)(j=1,2,…,n)为块体 i和块体 j之间相互作用形成的刚度矩阵,均为6×6矩阵;Di是一个6×1矩阵,为块体 i的位移变量;Fi是一个6×1矩阵,为块体i的等效荷载矩阵。
3.1.3 块体接触
因为大位移和大变形包含在非连续变形分析中,块体位置、块体形状和块体接触随荷载步和时间步在变化。在块体系统中,不允许块体之间受拉和嵌入。对每一种接触有3种模式:张开、滑动和锁定。
(1)当接触力沿边的垂直方向分量Rn为拉时,即Rn=-pd≤0,没有锁定或不用刚性弹簧。这种情况接触是张开的。
(2)当接触力的垂直分量Rn是压时,接触力沿进入线的剪切分量Rs足够大以致发生滑动时,Rs≥Rntanφ+c,用一个垂直于进入线的刚性弹簧容许进入边缘角发生滑动。用一对摩擦力作用在滑动方向,摩擦力用前一次迭代的法向力确定。
(3)当接触力的垂直分量Rn是压的且接触力沿进入线的剪切分量Rs小于库仑定律所得的摩擦力时,Rs<Rntanφ+c,接触点被垂直和剪切弹簧两者锁定并不容许滑动。
3.2 膨胀土边坡计算模型
以下结合本文算例,介绍如何建立膨胀土边坡的DDA计算模型。
3.2.1 块体划分
采用DDA分析边坡的稳定性,首先要根据边坡土体裂隙分布情况进行块体划分。膨胀土边坡经长期气候风化作用,浅层土体节理裂隙充分发育,通过现场统计只能知道表面裂隙分布,内部裂隙状况无法得知,所以无法进行现场统计建立地质裂隙模型。本文主要模拟膨胀土边坡浅层滑坡现象,根据边坡浅层破坏特征和Mohr-Coulomb准则,设置了3组潜在剪切破坏面,它们相互切割成块体。其中1组破坏面平行于坡面。
浅层土体的大主应力方向近似平行于坡面。根据摩尔库伦准则,另外2组潜在破坏面与坡面的夹角为
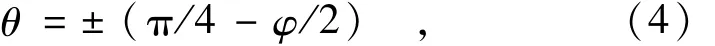
其中φ为膨胀土内摩擦角。
本文算例为南水北调中线工程一膨胀土边坡现场降雨试验段,坡高9.01 m,坡比 1∶1.5。该边坡土体以弱膨胀性泥灰岩为主,在累计人工降雨累计6 h左右时,发生了大面积滑坡,如图1。块体划分如图2所示。

图1 现场滑坡形态Fig.1 Landslide shape in field

图2 边坡块体系统Fig.2 Block system of slope
3.2.2 土体参数
本文主要研究表层膨胀土边坡吸湿膨胀的变形破坏过程。姚海林[7]和陈善雄、陈守义[2]通过现场试验测试降雨后膨胀土的含水率变化,结果表明膨胀土边坡含水率变化深度不超过3 m。膨胀土本身渗透性很小,降雨初始渗透主要通过膨胀土裂隙进行,而膨胀土遇水软化泥化,促使裂隙愈合,阻碍水向下渗透。
本文假设表层2 m深度内土体含水量相同,3 m以外膨胀土含水量保持不变,2~3 m深度范围内含水量呈线性变化。土体天然含水量9%,饱和含水量20%。
根据土工试验成果,土体参数如表1所示。风化层厚度按3 m考虑。参考有关资料,假定c,φ,E,μ和膨胀系数α均随w呈线性变化。因缺乏试验资料,本文算例E,μ,α不随含水量变化,其中E和α取为常数,如表1。

表1 膨胀土物理力学参数Table 1 Physical and mechanical parameters of an expansive soil
α与上覆压荷P有关。根据试验,P=0 kPa时,α=0.147;P=15 kPa时,α=0.050;P=25 kPa时,α=0.032。边坡土体的上覆压荷P按其埋深和重度确定。
3.2.3 本构方程
采用初应变法模拟吸湿膨胀变形的影响。在各计算时间步内假定材料参数为常数,增量形式的平面应力状态应力应变关系为

对于平面应变问题,式中E,μ,α应进行相应变换。
4 计算结果
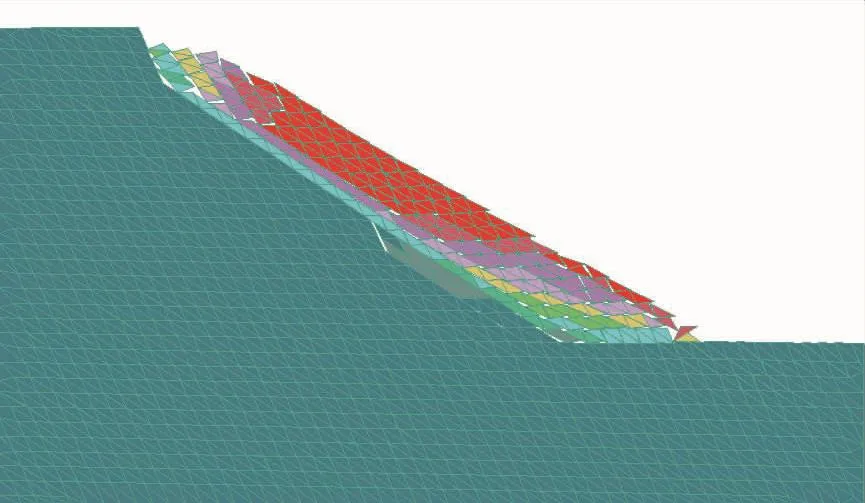
图3 DDA计算滑坡形态Fig.3 Landslide shape by DDA calculation

图4 边坡观测点水平位移曲线Fig.4 Horizontal displacement curves atmeasuring points

图5 边坡观测点垂直位移曲线Fig.5 Vertical displacement curves atmeasured points
采用 DDA动力计算过程,计算时间步长取0.005 s。先施加边坡土体自重,然后从天然含水量开始逐步分级增加土体含水量。每级含水量增量为0.5%,计算1 s后再施加下一级含水量增量。
土体含水量增加到一定程度时发生滑动破坏。破坏形态见图3,与现场破坏状态(图1)类似。滑坡厚度在2.3 m左右。
为了分析膨胀土边坡的破坏过程,选择了若干个观测点,如图2所示的A,B,C点。观测点位移随含水量变化如图4、图5所示。从图中可见,表层土体含水量小于15%时,各观测点位移都很小;含水量达到15%时,位移发生突变,边坡开始滑动。
含水量为14.5%和16.0%时的边坡位移矢量图分别如图6和图7所示。可见,边坡首先在坡角附近出现剪切破坏,从而引起上部土体失稳。

图6 含水量为14.5%时边坡位移矢量图Fig.6 Displacement vectors of slope with water content of14.5%

图7 含水量为16.0%时边坡位移矢量图Fig.7 Displacement vectors of slope with water content of16.0%
5 结 语
本文采用DDA模拟膨胀土边坡在吸湿膨胀和强度降低作用下的破坏过程,计算结果与膨胀土边坡现场降雨破坏试验得到的破坏现象类似,表明用DDA分析膨胀土边坡的破坏过程是可行的,本文建立的膨胀土边坡计算模型是合适的。本文工作为膨胀土边坡的稳定性分析开辟了新途径。笔者已用DDA分析了坡比、强度降低、膨胀率对膨胀土边坡稳定性的影响,得出了一些具有工程指导意义的结论,将另文发表。
[1] 刘特洪.工程建设中的膨胀土问题[M].北京:中国建筑工业出版社,1997.
[2] 陈善雄,陈守义.考虑降雨的非饱和土边坡稳定性分析方法[J].岩土力学,2001,22(4):447-450.
[3] 汪明元,徐 晗.非饱和膨胀土边坡破坏机理和稳定分析[J].南水北调与水利科技,2008,6(1):151-153.
[4] 张润峰,张献民,陈国明.基于DDA的强度折减法求土坡安全系数[J].中国民航大学学报,2007,25(3):45-48.
[5] 孙东亚,彭一江.DDA数值方法在岩质边坡倾倒破坏分析中的应用[J].岩石力学与工程学报,2002,21(1):39-42.
[6] 石根华,裴觉民.数值流形方法与非连续性变形分析[M].北京:清华大学出版社,1997.
[7] 姚海林,郑少河,葛修润,等.裂隙膨胀土边坡稳定性评价[J].岩石力学与工程学报,2002,21(2):2331-2335.

