时序规则表达法及其应用
[摘要]时序逻辑在许多领域如人工智能、形式化方法、自动控制中都有成功的应用。有效的实现系统控制在很大程度上取决于良好的系统状态表达法,时序规则表达法是综合基于时间点、区间、事件的时序逻辑的新方法。该方法可以简单、直观、有效的表达系统状态并可进行推理。将它应用于乙烯裂解炉温度控制系统中,可以获得很好的效果。
[关键词]时序逻辑 系统状态 时序规则
中图分类号:O29 文献标识码:A 文章编号:1671-7597(2009)0110127-02
一、引言
在标准逻辑中所讨论的命题是与时间无关的,既不涉及时态变化,也不涉及特定的参照空间,这些命题的真假是不受时间限制的[2]。与时态变化有关的命题及其推理用一般的标准逻辑是无法处理的。这也就是时序逻辑所要研究的。早在1960年,Quine就指出这类与时间相关的陈述应该用与时间无关的形式表达出来并用多序的谓词逻辑来进行推理。而Strason从另一个方面认为以上的现象预示着形式逻辑自身存在着限制性。上述是两种较消极的观点。第三种想法则更为积极,它主张将形式逻辑进行扩展,使得其能够解决该类问题。这种扩展的方法就是时序逻辑,它是处理与时间有关的推理问题的一类逻辑[5]。在时序逻辑中,相同句子在不同时刻有不同的值。在过去某时刻为真的句子可能现在不为真,现在为假的句子到将来某时刻可能为真。为了处理这种情况,可在任一命题前加上时序算子F,P,G,H就构成命题的时序语言lt。Lt的时序算子的直觉解释如下:
FA:A在将来某时刻为真; PA:A在过去某时刻为真;
GA:A在将来永远为真;HA:A在过去永远为真。
在此基础上,引进一个时序框架tf:tf=(T,R,h)是一个三元组,其中:T是非空的时间点集合;R是时序优先关系;h是一个函数:h:T×lt的原子子句>——1,0
Lt是扩充的命题演算语言,其语义可通过对函数h的赋值来解释,见[1]。根据对时序优先关系R的限制的不同,可得到各种不同的时序逻辑。如果不对R做任何的限制,则称此时的时序逻辑系统为极小系统,E.J.Lemmon将其命名为Kt,而其他时序逻辑系统都是Kt的扩充。如线性时序逻辑、分枝时态逻辑等。在这里将不作详细的介绍。
从对时间的表示来看,有基于时间点的时序逻辑;基于区间的时序逻辑,基于事件的时序逻辑。基于时间点的时序逻辑以McDermott为代表,他于1982年提出了一种时序逻辑,该逻辑的时序优先关系是及物的、左线性的、时间可以向两边无限延伸的、稠密的和连续的。他运用了带变量的多序的一阶谓词逻辑定义了“时间”、“状态”、“事实”、“事件”。而Allen的时序逻辑是基于区间的,他于1981年把两个时间点之间的一个时间区间,定义为时间原语[1](time atomic),并规定了两个时间区间的十三种不同关系。为了进行时序推理,他定义了五种区间之间的时序关系[1]。近年来,随着软件工程、人工智能的产生和发展,人们逐渐认识到时序逻辑对计算机科学的重要影响,1977年A.Pnueli首次将时态逻辑引入计算机科学。
目前计算机科学家已开发多种时态逻辑(语言),如Z.Manna和A.Pnueli
的PLTL、Chandy和Misrs的UNITY、唐稚松的XYZ/E、A.Lamprot的TLA、Emersom和Clarke的CTL/CTL^等,它们随时间结、时态算子的选择而异[6]。时序逻辑在系统控制领域的应用也十分广泛,这里所应用的时序逻辑即为基于系统状态的时序逻辑,该逻辑是将时序逻辑应用于系统状态控制中,通过对系统状态变量的时序描述和推理达到对系统状态的实时控制。下面将讨论如何将时序逻辑应用于系统状态控制。
二、基于系统状态的时序逻辑
(一)关于系统状态的定义
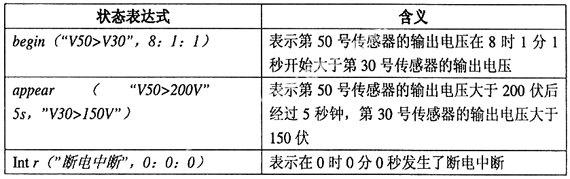
一个系统状态是过程或对象内部状态的反映,可通过系统状态变量在某段时间(时刻)的取值或改变来表征。这可用BNF(巴克斯范式)详细描述,参见[1]。下面的实例说明了该描述方法。如:用V50表示第50号传感器的输出电压,V30表示第30号传感器的输出电压,则如下式子表达的含义分别为:

由此可见,利用这种范式可以很好地将系统的状态进行表达。
(二)系统状态结构的定义
一个系统状态结构是一个代数系统E(V,A)[1]。上述基于系统状态的时序逻辑本质上是嵌入了时间因素的一阶谓词,是基于点的、基于区间的、基于时间的三种时序逻辑表示方法的综合运用。它允许把反映动态系统状态的运算表达式及其相关时间作为变量嵌入时序谓词,而时序谓词又可直接作为产生式规则的前件,因此可以简洁、直观的表达复杂的时变领域知识。对于上述的例子,如果嵌入时间因素,则变为:
三、基于时序规则的控制领域知识表达——时序规则法
(一)时序规则法的定义
针对系统控制领域的特殊性,有一种表达知识的新方法,即时序规则法。用于描述控制系统中若干对现象属性间的关系及控制规律,时序规则的基本形式是嵌套着时序关系谓词的扩展产生式规则,以BNF详细表达,参照[1]。
(二)裂解炉控温系统的时序规则法表达及推理
裂解炉是乙烯生产的主要设备之一,在乙烯生产过程中,必须对裂解炉进行控制。其控制变量较多且大多与时间有关,如炉管出口温度(OCT)、进料量、稀释蒸汽流量、烧嘴压力等的控制均在一定的时间条件下进行。因此,有关裂解炉控制的知识是包含时间因素的知识,可以应用时序规则法表达。首先设定如下状态变量:
Close_t——表示闭环回路温度测量值
open_t ——表示开环回路温度测定值
set_t——表示设定值
fm5_status——表示5号烧嘴的状态,on 表示接通;off表示切断
S表示秒,m表示分
在裂解炉控制中,如OCT出现异常高温,就要执行如下的切断烧嘴的控制动作:
Case1:
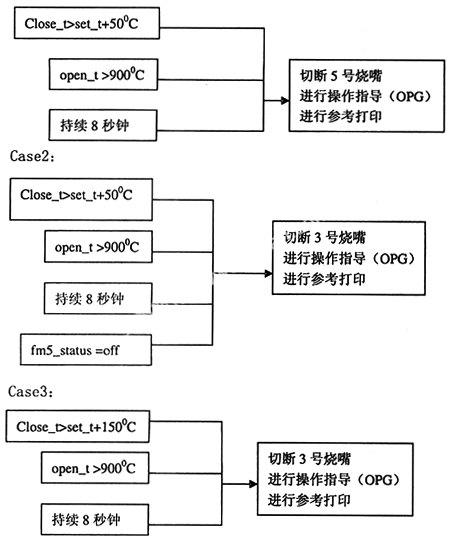
用时序规则法表达见[1]。下面将运用上述的表达进行推理。为了能更好地理解推理过程,即控制系统如何根据所得到的事实进行推理,从而达到控制的目的,需要介绍一下该控制系统是如何获得事实的。在裂解炉控温系统中,推理所需要的事实包括:
设定值(set_t):这是一个参考变量,温度的高低需要和该值进行比较才能确定。同时该值较为固定,因此可用事实三元组来表示。假设set_t=300℃,则F(温度设定值,温度,300℃)就表达了该参量。
闭环回路温度测定值(close_t)和开环回路温度测定值(open_t):这两者是系统状态变化,它们随时间的变化不断变化,所以要获取该事实就需要相应的硬件设备用于较精确且及时的测定,然后将测定结果送入控制器。
持续时间测定:高温所持续的时间是采取相应控制动作的一个重要因素,如果只是瞬间的高温,可以认为是测定误差或其他原因所致,而且高温持续时间较短,对系统不会产生很大影响,因此该系统必须要获取高温持续时间值,然后判断究竟有没有持续高温(即是否大于8秒)。这里需要注意的问题是,close_t和open_t必须同时满足高温条件,才会采取动作。所以系统必须设定两个计时器分别对两个变量计时,只有当它们都大于等于8秒时才能满足条件。所以要获取该事实除了需要硬件(计时器)外,还需要一个判断高温的程序。现在假定所用的事实都可以获取,系统将如何根据事实进行推理?看如下的例子:

所以执行相应动作: 切断5号烧嘴
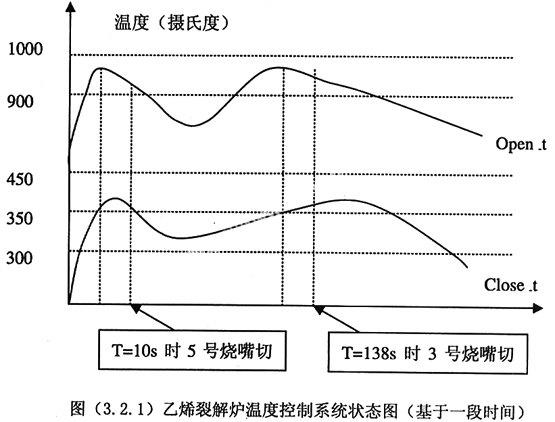
随着时间的推移,事实是不断变化的,于是这个推理的过程也不断的进行,整个推理的过程就起到了控温的作用。图(3.2.1)给出了在一段时间内该控制系统是如何控制高温的。
从close_t 和open_t曲线变化中可以得到:open_t比close_t先达到高温状态。在t=2s时两者均达到高温,并一直持续了8s,故此时匹配规则r1,将5 号烧嘴切断(这时fm5_stasus=on),经过2分钟,当t=130s时,两个变量又同时达到高温状态,匹配规则r2,将3号烧嘴切断。具体请参照图示。从该例子可见,运用时序规则法可以较为准确、方便的进行系统控制。
四、结论
本文就应用时序逻辑进行系统状态的控制提了时序规则法,该方法可以较为快速、准确的解决某方面的系统控制问题,如文中所举的乙烯裂解炉温度控制问题。该方法是综合了基于点、区间、事件的时序逻辑提出的新方法,在推理不太复杂的控制系统中可以很好地应用,但是如果系统的状态较为复杂,则推理的困难程度增加,效率将会降低。所以进一步的工作是将该表达法与神经网络结合起来,用该表达法作为智能系统的一种外部知识表达方法,推理将通过神经网络的并行处理来进行。这样,既可以克服经典时序逻辑效率低的缺点,又能发挥它直观表达时序知识的优点。
参考文献:
[1]邵军力、张景、魏长华,人工智能基础[M].北京:电子工业出版社,2000.3.
[2]王雨田,现代逻辑科学导轮[M].北京:中国人民大学出版社,1988.3.
[3]胡成军、王戟,区间时序逻辑的标记相继式演算[M].北京:计算机学报,1999.11(22).
[4]Dov M.GABBAY, C. J.HOGGER.Handbook of logic in Atificial Intelligence and Logic Programming. Oxford Science Publications,1994.
[5]Raymono Turner.Logics For Artifical Intelligence.Halsted.Press in Great Britain,1984.
[6]张广泉、戎玫,时态逻辑与并发程序[M].重庆:重庆大学学报(自然科学版),1999.1.
作者简介:
李聪睿,男,副教授,主要研究方向:应用数学、数学教育。

